Hash表分析

Hash表中的一些原理/概念，及根据这些原理/概念:

一.       Hash表概念

二.       Hash构造函数的方法，及适用范围

三.       Hash处理冲突方法，各自特征

四.       Hash查找过程

五.       实现一个使用Hash存数据的场景-------Hash查找算法，插入算法

六.       JDK中HashMap的实现

七.       Hash表与HashMap的对比，性能分析

 

 一.    Hash表概念 

               在查找表中我们已经说过，在Hash表中，记录在表中的位置和其关键字之间存在着一种确定的关系。这样       我们就能预先知道所查关键字在表中的位置，从而直接通过下标找到记录。使ASL趋近与0.

 

              1)   哈希(Hash)函数是一个映象，即： 将关键字的集合映射到某个地址集合上，它的设置很灵活，只要这个地址集合的大小不超出允许范围即可；

             2)  由于哈希函数是一个压缩映象，因此，在一般情况下，很容易产生“冲突”现象，即： key1¹ key2，而  f (key1) = f(key2)。

              3).  只能尽量减少冲突而不能完全避免冲突，这是因为通常关键字集合比较大，其元素包括所有可能的关键字，而地址集合的元素仅为哈希表中的地址值

 

       在构造这种特殊的“查找表” 时，除了需要选择一个“好”(尽可能少产生冲突)的哈希函数之外；还需要找到一种“处理冲突” 的方法。

 

二 .     Hash构造函数的方法，及适用范围

• 直接定址法
• 数字分析法
• 平方取中法
• 折叠法
• 除留余数法
• 随机数法      

 

      （1）直接定址法：

                哈希函数为关键字的线性函数，H(key) = key 或者 H(key) = a ´ key + b

              此法仅适合于：地址集合的大小 = = 关键字集合的大小，其中a和b为常数。

     （2）数字分析法：

             假设关键字集合中的每个关键字都是由 s 位数字组成 (u₁, u₂, …, u_s)，分析关键字集中的全体， 并从中提取分布均匀的若干位或它们的组合作为地址。

             此法适于:能预先估计出全体关键字的每一位上各种数字出现的频度。

     （3）平方取中法：

               以关键字的平方值的中间几位作为存储地址。求“关键字的平方值” 的目的是“扩大差别” ，同时平方值的中间各位又能受到整个关键字中各位的影响。

             此法适于:关键字中的每一位都有某些数字重复出现频度很高的现象。

     （4）折叠法：

            将关键字分割成若干部分，然后取它们的叠加和为哈希地址。两种叠加处理的方法：移位叠加:将分割后的几部分低位对齐相加；间界叠加:从一端沿分割界来回折叠，然后对齐相加。

            此法适于：关键字的数字位数特别多。

     （5）除留余数法：

             设定哈希函数为:H(key) = key MOD p   ( p≤m )，其中， m为表长，p 为不大于 m 的素数，或是不含 20 以下的质因子

     （6）随机数法：

           设定哈希函数为:H(key) = Random(key)其中，Random 为伪随机函数

           此法适于：对长度不等的关键字构造哈希函数。

 

         实际造表时，采用何种构造哈希函数的方法取决于建表的关键字集合的情况(包括关键字的范围和形态)，以及哈希表    长度（哈希地址范围），总的原则是使产生冲突的可能性降到尽可能地小。

三.       Hash处理冲突方法，各自特征

 “处理冲突” 的实际含义是：为产生冲突的关键字寻找下一个哈希地址。

•   开放定址法
•   再哈希法
•   链地址法

      （1）开放定址法：

               为产生冲突的关键字地址 H(key) 求得一个地址序列： H₀, H₁, H₂, …, H_s  1≤s≤m-1，H_i = ( H(key)+d_i  ) MOD m，其中： i=1, 2, …, s，H(key)为哈希函数;m为哈希表长;

 

      （2）链地址法：

             将所有哈希地址相同的记录都链接在同一链表中。

 

      （3）再哈希法：

               方法：构造若干个哈希函数，当发生冲突时，根据另一个哈希函数计算下一个哈希地址，直到冲突不再发生。即：H_i=Rh_i(key)     i=1,2,……k，其中：Rh_i——不同的哈希函数，特点：计算时间增加

 四.       Hash查找过程

        对于给定值 K,计算哈希地址 i = H(K)，若 r[i] = NULL  则查找不成功，若 r[i].key = K  则查找成功， 否则 “求下一地址 Hi” ，直至r[Hi] = NULL  (查找不成功)  或r[Hi].key = K  (查找成功) 为止。

 

 五.       实现一个使用Hash存数据的场景-------Hash查找算法，插入算法

         假设我们要设计的是一个用来保存在校学生个人信息的数据表。因为在校学生数量也不是特别巨大(8W?)，每个学生的学号是唯一的,因此，我们可以简单的应用直接定址法，声明一个10W大小的数组，每个学生的学号作为主键。然后每次要添加或者查找学生，只需要根据需要去操作即可。

      但是，显然这样做是很脑残的。这样做系统的可拓展性和复用性就非常差了，比如有一天人数超过10W了？如果是用来保存别的数据呢？或者我只需要保存20条记录呢？声明大小为10W的数组显然是太浪费了的。

 

     如果我们是用来保存大数据量（比如银行的用户数，4大的用户数都应该有3-5亿了吧？），这时候我们计算出来的HashCode就很可能会有冲突了， 我们的系统应该有“处理冲突”的能力，此处我们通过挂链法“处理冲突”。

 

     如果我们的数据量非常巨大，并且还持续在增加，如果我们仅仅只是通过挂链法来处理冲突，可能我们的链上挂了上万个数据后，这个时候再通过静态搜索来查找链表，显然性能也是非常低的。所以我们的系统应该还能实现自动扩容，当容量达到某比例后，即自动扩容，使装载因子保存在一个固定的水平上。

什么时候ReHash

在介绍HashMap的内部实现机制时提到了两个参数，DEFAULT_INITIAL_CAPACITY和DEFAULT_LOAD_FACTOR，DEFAULT_INITIAL_CAPACITY是table数组的容量，DEFAULT_LOAD_FACTOR则是为了最大程度避免哈希冲突，提高HashMap效率而设置的一个影响因子，将其乘以DEFAULT_INITIAL_CAPACITY就得到了一个阈值threshold，当HashMap的容量达到threshold时就需要进行扩容，这个时候就要进行ReHash操作了，可以看到下面addEntry函数的实现，当size达到threshold时会调用resize函数进行扩容。

void addEntry(int hash, K key, V value, int bucketIndex) {  
ntry<K,V> e = table[bucketIndex];  
      table[bucketIndex] = new Entry<K,V>(hash, key, value, e);  
      if (size++ >= threshold)  
          resize(2 * table.length);  
  }  

在扩容的过程中需要进行ReHash操作，而这是非常耗时的，在实际中应该尽量避免。

 

Bloom Filter概念和原理

 

Bloom Filter是一种空间效率很高的随机数据结构，它利用位数组很简洁地表示一个集合，并能判断一个元素是否属于这个集合。Bloom Filter的这种高效是有一定代价的：在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误认为属于这个集合（false positive）。因此，Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter通过极少的错误换取了存储空间的极大节省。

集合表示和元素查询

下面我们具体来看Bloom Filter是如何用位数组表示集合的。初始状态时，Bloom Filter是一个包含m位的位数组，每一位都置为0。

为了表达S={x₁, x₂,…,x_n}这样一个n个元素的集合，Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x，第i个哈希函数映射的位置h_i(x)就会被置为1（1≤i≤k）。注意，如果一个位置多次被置为1，那么只有第一次会起作用，后面几次将没有任何效果。在下图中，k=3，且有两个哈希函数选中同一个位置（从左边数第五位）。   

 

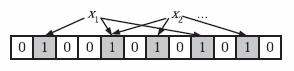
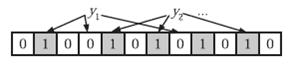
在判断y是否属于这个集合时，我们对y应用k次哈希函数，如果所有h_i(y)的位置都是1（1≤i≤k），那么我们就认为y是集合中的元素，否则就认为y不是集合中的元素。下图中y₁就不是集合中的元素。y₂或者属于这个集合，或者刚好是一个false positive。

错误率估计

前面我们已经提到了，Bloom Filter在判断一个元素是否属于它表示的集合时会有一定的错误率（false positive rate），下面我们就来估计错误率的大小。在估计之前为了简化模型，我们假设kn<m且各个哈希函数是完全随机的。当集合S={x₁, x₂,…,x_n}的所有元素都被k个哈希函数映射到m位的位数组中时，这个位数组中某一位还是0的概率是：

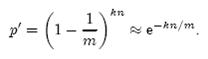
其中1/m表示任意一个哈希函数选中这一位的概率（前提是哈希函数是完全随机的），(1-1/m)表示哈希一次没有选中这一位的概率。要把S完全映射到位数组中，需要做kn次哈希。某一位还是0意味着kn次哈希都没有选中它，因此这个概率就是（1-1/m）的kn次方。令p = e^-kn/m是为了简化运算，这里用到了计算e时常用的近似：

 

令ρ为位数组中0的比例，则ρ的数学期望E(ρ)= p’。在ρ已知的情况下，要求的错误率（false positive rate）为：

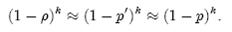
(1-ρ)为位数组中1的比例，(1-ρ)^k就表示k次哈希都刚好选中1的区域，即false positive rate。上式中第二步近似在前面已经提到了，现在来看第一步近似。p’只是ρ的数学期望，在实际中ρ的值有可能偏离它的数学期望值。M. Mitzenmacher已经证明^[2] ，位数组中0的比例非常集中地分布在它的数学期望值的附近。因此，第一步的近似得以成立。分别将p和p’代入上式中，得：

   

   

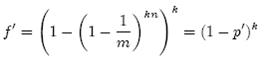
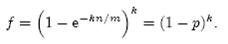
相比p’和f’，使用p和f通常在分析中更为方便。

最优的哈希函数个数

既然Bloom Filter要靠多个哈希函数将集合映射到位数组中，那么应该选择几个哈希函数才能使元素查询时的错误率降到最低呢？这里有两个互斥的理由：如果哈希函数的个数多，那么在对一个不属于集合的元素进行查询时得到0的概率就大；但另一方面，如果哈希函数的个数少，那么位数组中的0就多。为了得到最优的哈希函数个数，我们需要根据上一小节中的错误率公式进行计算。

 

先用p和f进行计算。注意到f = exp(k ln(1 − e^−kn/m))，我们令g = k ln(1 − e^−kn/m)，只要让g取到最小，f自然也取到最小。由于p = e^-kn/m，我们可以将g写成

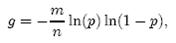
根据对称性法则可以很容易看出当p = 1/2，也就是k = ln2· (m/n)时，g取得最小值。在这种情况下，最小错误率f等于(1/2)^k ≈ (0.6185)^m/n。另外，注意到p是位数组中某一位仍是0的概率，所以p = 1/2对应着位数组中0和1各一半。换句话说，要想保持错误率低，最好让位数组有一半还空着。

 

需要强调的一点是，p = 1/2时错误率最小这个结果并不依赖于近似值p和f。同样对于f’ = exp(k ln(1 − (1 − 1/m)^kn))，g’ = k ln(1 − (1 − 1/m)^kn)，p’ = (1 − 1/m)^kn，我们可以将g’写成

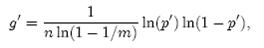
同样根据对称性法则可以得到当p’ = 1/2时，g’取得最小值。、

位数组的大小

下面我们来看看，在不超过一定错误率的情况下，Bloom Filter至少需要多少位才能表示全集中任意n个元素的集合。假设全集中共有u个元素，允许的最大错误率为є，下面我们来求位数组的位数m。

 

假设X为全集中任取n个元素的集合，F(X)是表示X的位数组。那么对于集合X中任意一个元素x，在s = F(X)中查询x都能得到肯定的结果，即s能够接受x。显然，由于Bloom Filter引入了错误，s能够接受的不仅仅是X中的元素，它还能够є (u - n)个false positive。因此，对于一个确定的位数组来说，它能够接受总共n + є (u - n)个元素。在n + є (u - n)个元素中，s真正表示的只有其中n个，所以一个确定的位数组可以表示

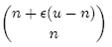
个集合。m位的位数组共有2^m个不同的组合，进而可以推出，m位的位数组可以表示

   

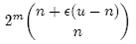
个集合。全集中n个元素的集合总共有

   

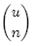
个，因此要让m位的位数组能够表示所有n个元素的集合，必须有

   

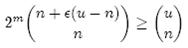
即：

   

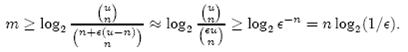
上式中的近似前提是n和єu相比很小，这也是实际情况中常常发生的。根据上式，我们得出结论：在错误率不大于є的情况下，m至少要等于n log₂(1/є)才能表示任意n个元素的集合。

 

上一小节中我们曾算出当k = ln2· (m/n)时错误率f最小，这时f = (1/2)^k = (1/2)^{mln2 / n}。现在令f≤є，可以推出

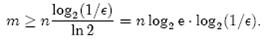
这个结果比前面我们算得的下界n log₂(1/є)大了log₂ e ≈ 1.44倍。这说明在哈希函数的个数取到最优时，要让错误率不超过є，m至少需要取到最小值的1.44倍。

总结

在计算机科学中，我们常常会碰到时间换空间或者空间换时间的情况，即为了达到某一个方面的最优而牺牲另一个方面。Bloom Filter在时间空间这两个因素之外又引入了另一个因素：错误率。在使用Bloom Filter判断一个元素是否属于某个集合时，会有一定的错误率。也就是说，有可能把不属于这个集合的元素误认为属于这个集合（False Positive），但不会把属于这个集合的元素误认为不属于这个集合（False Negative）。在增加了错误率这个因素之后，Bloom Filter通过允许少量的错误来节省大量的存储空间。

 

自从Burton Bloom在70年代提出Bloom Filter之后，Bloom Filter就被广泛用于拼写检查和数据库系统中。近一二十年，伴随着网络的普及和发展，Bloom Filter在网络领域获得了新生，各种Bloom Filter变种和新的应用不断出现。可以预见，随着网络应用的不断深入，新的变种和应用将会继续出现，Bloom Filter必将获得更大的发展。