欧拉函数 简单题

$\phi (n)$ 表示 $n$ 以内和 $n$ 互质的数的个数

• 若 $n$ 为质数 $\phi (n)=n-1$
• $\phi (p^k)=p^k-p^{k-1}=p^k(p-1)$
• $\phi (n)$ 为积性函数，也就是若 $a,b$ 互质，则 $\phi (ab)=\phi (a)\phi (b)$
• ${\sum }_{d|n}\phi (d)=n$
• 欧拉定理：若 $a,m(m\ge 2)$ 互质，$a^{\phi (m)}\equiv 1(\mathrm{mod}m)$
• 费马小定理：欧拉定理特殊形式，在 $m$ 为质数时，$a^{m-1}\equiv 1(\mathrm{mod}m)$

T1

设 $f(n)$ 为 $n$ 的因数个数，答案就是 $n-\phi (n)-f(n)+1$

加1时因为1被算了2次

T2

考虑一个位置被看到，则有 $\gcd (x,y)=1$。对于一个定的 $y$，合法 $x$ 数就是 $\phi (y)$

T3

易发现一个数如果含有一个因子属于 $[2,m]$，则不合法。而且我们可以缩小范围，不能包含 $[2,m]$ 内的质因子，设为 {p}\{p\}{p}。

类比欧拉函数计算公式，答案即为 $n!{\prod }_{i=1}^n(1-\frac{1}{p_i})$

T4

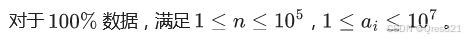
容易发现我们把一个 $a$，当成两个 $p_1,p_2$ 的 $a$ 来计算，是不影响的。

然后根据欧拉函数的积性，我们把所有质数分开来算是不影响的，现在等价于求 ${\sum }_{i_1|p^{c_1}}{\sum }_{i_2|p^{c_2}}{\sum }_{i_3|p^{c_3}}\dots \phi (\prod i)$

显然，只要里面那个prod非0，那么其实就等价于他们的积成 $\frac{p-1}{p}$，因此相互之间独立，直接乘起来即可

答案即为：$$\prod _p(\frac{(p-1)({\prod }_i{\sum }_{j=0}^i{p}^i-1)}{p}+1)$$

拓展欧拉定理

$$a^b\equiv a^{b\mathrm{mod}\phi (p)+\phi (p)}(\mathrm{mod}p)$$

其中，若 $a,p$ 互质，则 $$a^b\equiv a^{b\mathrm{mod}\phi (p)}$$（这个直接用欧拉定理就可以证明了）

我们发现对于 $b\mathrm{mod}\phi (p)$ 的样子，一定形如一种混循环：

如果我们不加 $\phi (p)$，我们就可能无法进入的循环里，所以我们要多加一个 $\phi (p)$ 来保证进入圈内从而保证正确性。

需要注意的是，在 $b<\phi (p)$ 时，我们指数项不应该加上 $\phi (p)$，以下是一组反例 $a=2,p=4,b=1$。

T5

不妨设 $r_p=2^{2^{2^{2\dots }}}\mathrm{mod}p$，根据扩展欧拉定理有：

$$r_p\equiv 2^{2^{2^{2^{2\dots }}}\mathrm{mod}\phi (p)+\phi (p)}(\mathrm{mod}p)$$

$$r_p\equiv 2^{2_{\phi (p)}+\phi (p)}(\mathrm{mod}p)$$

递归解决即可