NOIP前题目整理

动态规划/dp

常见类型

背包

背包类最经典的一类dp问题。

容量很大体积很小的背包问题

• 完全背包 https://www.luogu.com.cn/problem/P9140
• 多重背包 http://zhengruioi.com/problem/2620

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132216843

核心思想：先选性价比高的，剩余空间自行调整。

对于多重背包，我们要维护一个反悔贪心的过程，其重量和价值都为负。

[ABC321F] #(subset sum = K) with Add and Erase 可删除背包

题目 https://www.luogu.com.cn/problem/AT_abc321_f

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133219375

考虑把背包展开，变成二维转移的形式

然后我们把这个过程逆过来即可

颜色类

P9561 [SDCPC2023] Colorful Segments （考虑颜色切换）

题目：https://www.luogu.com.cn/problem/P9561

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132471731

我们可以设 $dp[i][0/1]$，但从 $dp[j][0]$ 到 $dp[i][0]$，对于 $j$ 前的1，可能 $j$ 满足，但 $i$ 不满足

此时可以考虑0只从1转移，1只从0转移，对于新的0，我们除了统计当前dp值，我们还要维护之前1的转移值

0919B 摘抄文档 copy （颜色扩散+颜色互异相等）

题目 http://cplusoj.com/d/senior/p/330

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133047170

颜色属于扩散类，有个很显然的性质：扩散后颜色的相对顺序不会改变。

然后 $f_{i,j}$ 第 $i$ 个位置用 $c_j$ 色的dp直接后缀和优化就行了。

但是相对顺序不会改变，就一定可以覆盖到吗？我们只需要让当前的 $i$ 在 $j$ 的合法扩散区间 $[l_j,r_j]$ 里就行了。

对于 $c_i$ 互异的情况，显然 $b_i=c_i$ 的情况最多 $n$ 次，我们拿个线段树优化即可。具体的，我们在 $j$ 位置对 $[j+1,n]$ 的mx+1即可。

计数类

计数类dp的核心是dp，不是数数

但和其他计数类题目一样，关键不重不漏

ABC299F（子序列自动机）

题目：https://www.luogu.com.cn/problem/AT_abc299_f

子序列自动机+dp。本题很容易重复。

本题做到不重复的关键在于令子序列自动一个结尾的nxt恰为另一个的开头

0903T3 习惯孤独lone（计数dp+树形dp+状压dp）

题目 http://www.accoders.com/pdf/contest/4498.pdf

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132647373

首先操作数 $k\le 6$，考虑对操作进行状压，然后丢树上进行树形dp。

对于每棵子树，我们更新上面那条是否割。若割，则有两种可能：保留 / 删掉。

如果删除，那么子树不能有保留操作，且所有删除操作都早于当前删除操作。

如果保留，那么剩下所有操作都必须在子树内进行，且子树所有保留操作都必须晚于当前操作。

[ARC146E] Simple Speed （从小往大插数+分析dp状态）

题目 https://www.luogu.com.cn/problem/AT_arc146_e

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132794937

我们可以从小往大插数，可以设计 $dp[i][j][0/1/2]$ 表示前 $i$ 个数，第 $i$ 个有 $j$ 个相邻的，左右两边有多少个为 $i$

此时状态是 $O(n^2)$ 的。但打表分析可得dp的转移过程很单一，相邻之间的转移相差也就1，而且第三维是类似一种层数的东西，只能从高层到低层。

此时大胆猜测状态数并不多。手玩一下可以发现，在第一、三维确定时，第二维的取值只有3种，然后记搜就完事了

0909T3 消失的运算符operator（双记录dp）

题目 http://www.accoders.com/problem.php?cid=4501&pid=2

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132796834

首先括号的限制可以建树去掉

我们可以记录 $[j](dp,g)$ 表示所以情况的值和末尾乘积。

转移时分讨然后乘个组合数即可

CF1762F Good Pairs （值域和位置同时考虑）

题目 https://www.luogu.com.cn/problem/CF1762F

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133691573

显然要么一直向上，要么一直向下，我们现在先考虑向上。

设 $f_i$ 表示 $i$ 点答案，从后往前，先找第一个 $j>i,a_j>a_i$ 的位置，由 $f_j$ 转移过来。

看看我们漏掉了什么，$[a_i,a_j-1]$ 里的数，拿个ds维护即可 。

概率期望类

0914T4D. 排水系统water （期望可加性）

题目 http://cplusoj.com/d/senior/p/SS230913D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132857701

因为DAG，所以dp。设 $d{p}_i$ 表示路径上没有遇到过断边的流量（因为其他地方断边对流量无影响），$f_i$ 表示断了一条的期望流量。$dp$ 暴力转移即可，只是要乘个没断边的概率。

$f$ 可以直接由 $f$ 转移过来，也可以由 $dp$ 转移过来，但注意分类讨论是哪条边断，计算其概率和对当前的影响即可。以 $dp\to f$为例：

$$f_j=\sum _{j\to i}d{p}_j(\frac{a_{j,i}}{\sum a}\times 0+\frac{S_j-a_{j,i}}{\sum a}\times \frac{1}{d_j-1})$$

CF494C Helping People （概率转整数+状态分析）

题目 https://www.luogu.com.cn/problem/CF494C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133343917

发现区间无交错，显然可以建树。然后发现一个区间的最大值最多只有子树大小种。

$dp(i,j)$ 表示 $i$ 子树内最大值 $\ge j$ 的概率，很容易转移。最后做个差分即可，乘起来就是期望了。

CF1392H ZS Shuffles Cards （从排列角度考虑操作顺序）

题目 https://www.luogu.com.cn/problem/CF1392H

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133355060

考虑在 $m$ 张牌里插 $n$ 张牌，所以一轮期望次数是 $\frac{n}{m+1}+1$

设 $f(i)$ 表示还剩 $i$ 张牌抽到新牌的期望失败轮数。我们只考虑这 $m+i$ 张牌的所有排列，我们想先抽到一张 $i$ 里的牌概率是 $\frac{i}{m+i}$，所以期望 $\frac{m+i}{i}-1$，减1是因为我们要算的是失败轮数。

所以总轮数应为 $\sum f(i)+1$

CF536D Tavas in Kansas （图论+博弈论+dp）

题目 https://www.luogu.com.cn/problem/CF536D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133364509

可以先离散化，然后设 $f(i,j,0/1)$ 表示一个人已选 $\le i$，另一个已选 $\le j$，剩余先手的最大值。然后预处理一下 $s(x,y),c(x,y)$ 即可。比如先手可以由 $i^{\prime }\to i(i^{\prime }>i)$，我们要的是 $f(i^{\prime },j,0)+s(i^{\prime },j)-s(i,j)$ 的最大值，且 $c(i^{\prime },j)-c(i,j)>0$。

部分和优化一下即可。

对于从三个方向转移的期望dp式子移项方法

https://blog.csdn.net/zhangtingxiqwq/article/details/133753059

$f_i=a{f}_{i-1}+b{f}_i+c{f}_{i+1}+v_i$，其中 $a+b+c=1$ ，求 $f$

考虑差分，$g_i=f_i-f_{i+1}$

$f_i=a(f_{i-1}+g_{i-1})+b{f}_i+c(f_{i-1}-g_i)+v_i$

注意到 $a+b+c=1$，因此可以把 $f$ 消掉

$0=g_{i-1}a-c{g}_i+v_i$

然后就可以推出 $g$ 的递推式，然后反求 $f$ 即可

CF1349D Slime and Biscuits （拆贡献+期望+容斥）

题目 https://www.luogu.com.cn/problem/CF1349D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133753187

• 首先可以拆成每个人的期望步数（这个步数包括他们自己本身赢的概率），设为 $E(i)$，因此我们最后就是要求 $\sum E(i)$
• 每个人赢的概率和期望步数只和自己当前饼干数和总饼干数有关。因此我们可以设 $f_i$ 表示当前持有 $i$ 块饼干赢的期望步数。
• 我们发现要钦定某个人先赢且其他人不赢的概率很难，但我们可以直接计算一个人拿完所有饼干猜结束的期望步数，设为 $E^{\prime }(i)$，然后减掉别人先赢的期望步数。也就是减去 ${\sum }_{j\ne i}(E(j)+P(j)\times C)$，其中 $C$ 表示从一个人完全转移的到另一个人的期望步数，显然 $C=f_0$
• 我们现在有 $E(i)=E^{\prime }(i)-{\sum }_{j\ne i}(E(j)+P(j)\times C)$，其中 $E^{\prime }(i)=f_{a_i}$，理论上我们可以直接高消，但数据范围接受不了，而且也很麻烦。但观察到我们只需要求 $\sum E(i)$，我们可以直接把所有式子加起来，发现所有 $E$ 可以合并起来，变成了一个单纯关于 $\sum E(i)$ 的式子。
• 现在我们只需要求 $f$ 即可。我们直接分类讨论当前饼干由谁转移出去，转移到谁那，然后这是一个三个方向的dp，用上面章节的知识可以优化。

状压dp

0912C. 绘画（状压dp维护进位——从后往前）

题目 http://cplusoj.com/d/senior/p/SS230912C?tid=64ffe834f5f3679386f2da4b

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132840291

考虑题目转化，二进制下满足 $i\&j=0,(i+x)\&(j+y)=0$

对于这个转化后的条件，我们就应该直接套数位dp了。但我们发现一个问题，后面的那个式子会有进位，怎么办？

我们可以从低位往高位dp。设 $dp(x,i,j)$ 表示到达第 $x$ 位，前面分别进位 $i,j$ 的方案数。我们枚举值 $p1,p2$，算出进位后的值 $q1,q2$，满足两个与都为0，然后再计算出新的进位 $n1,n2$ 即可。

CCPC 2020 长春站J（状压dp优化转移状态）

题目 https://vjudge.net/contest/587311#problem/G

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133855597

状压dp很显然，只需要状态10位就行，但这样复杂度是 $O(n{2}^{20})$ 的。

发现我们在这里放圆，圆长度必然为偶数，因此转移可以优化到 $O(2^5)$，总复杂度 $O(n{2}^{15})$

CF1767E Algebra Flash （折半+考虑超集）

题目 https://www.luogu.com.cn/problem/CF1767E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133607589

观察数据范围可知道是折半，但折完半呢？我们分析题目性质，发现关键在于任意两个相邻格子至少选1个。

因此但我们决定了其中一半的时候，我们可以求其已经确定位置的超集，表示哪些位置还没有进行覆盖。而这一部分的最小代价我们在另一边折半的时候已经计算了。

数学类

ZR2639三色堇（枚举新增贡献）

题目：http://zhengruioi.com/problem/2639

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132325425

我们考虑逐个加入质数，然后维护新增贡献。

我们可以先设 $f(i)$ 表示差值为 $i$ 有多少种。现在每个差值都翻了 $k$ 倍，而且其开头恰好取遍 $0\dots p-1$，也就是我们切断每个段的贡献是一样的。

有 $j-1$ 种情况被切断，贡献到 $1\sim j-1$，贡献为2。因此有 $p-j+1$ 种情况贡献给自己

平移类

平移类dp不常见，但出了就是不会

ZR23ABDay6 测测你的签到水平

题目：http://zhengruioi.com/problem/2617

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132240791

我们要计算这样的dp：

$$d{p}_{i,j}=\sum d{p}_{k,j-w(k,i)}$$

如果 $w$ 我们只会进行区间修改，我们就可以拿线段树维护。我们在对应区间把dp进行位移。

相当于我们把平移的内容拆成一段段来进行，对应线段树一个个区间。

数位dp

Loj #6274. 数字

题目 https://loj.ac/p/6274

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132950029

暴力数位dp，$dp(k,0/1,0/1,0/1,0/1)$ 表示从高往低第 $k$ 位，和一堆上下界限制。

在满足或值相同的情况下，如果与值相同，我们去max即可。为什么？

首先如果当前无上下界限制，那么下一位肯定也没上下界限制，任取即可（因为我们只关心与值）

如果有其中一个上下界限制，那么其中一种选法必然可以推出无限制

假如两个都有上下界限制，选法只能是 （0,1）和（1,0），那样子怎么选没区别。

如果其中一个有上下界限制，考虑下一位或值，如果为0那么只能为0。如果为1我们就令其为1，那么没限制那边就可以自由控制与值了。

CF1734F Zeros and Ones （popcount性质dp+从低往高位dp）

题目 https://www.luogu.com.cn/problem/CF1734F

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133749334

$s_i$ 就只和 $i$ 的popcount有关。

popcount有个性质：popcount(x)^popcount(y)=popcount(x^y)

因此我们需要计算 ${\sum }_{i=0}^m\text{popcount}(i\oplus (i+n))$，因为这是一个涉及进位的数位dp，所以我们要从低往高位dp

区间dp

CF1107E Vasya and Binary String （巧妙涉及状态优化区间dp转移）

题目 https://www.luogu.com.cn/problem/CF1107E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133759674

朴素思路是设 $dp(l,r,k,0/1)$，然后枚举分界点和左边0/1的数量来转移，复杂度是 $O(n^5)$ 的。

我们考虑哪里可以优化，发现转移有两个，很浪费。我们考虑只能从 $k-1$ 转移到 $k$，因此我们就钦定这 $k$ 个0/1都是在靠最右边，然后那我们只需要找第一个 $a_j=0/1$ 的位置，从 $dp(l,j,k-1)$ 转移过来即可。

1017C. 蛋糕（cake） （讨论最值点决定分界点）

题目 http://cplusoj.com/d/senior/p/SS231017C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133884752

考虑一个朴素 $dp(l,r,k)$ 代表 $[l,r]$ 已经减掉 $k$ 剩余部分的最小代价。

转移有两种方法，枚举分界点 $mid$，或者整体-1转移到 $k+1$。

这两种其实都可以优化。考虑区间最大值，如果最大值选了，那直接选整个区间肯定最优。所以如果最大值不选，它肯定是单独一列，往两边分别递归就行。

如果整体减，我们就减一部分是没意义的，肯定是建到最矮高度。然后我们从最矮高度往两边递归即可。

整数划分

用 $j$ 个数表示 $i$ 的方案数。

转移考虑最小值是否为1

无限制

1. 若为1，则转移到 $f(i+1,j+1)$
2. 不为1，则全部+1，转移到 $f(i+j,j)$

数之间不能重复

那么相当于每次整体+1

1. 若为1，转移到 $f(i+j+1,j+1)$
2. 不为1，转移到 $f(i+j,j)$

数的上界有限制

考虑 $f(i,j)$ 所有数都合法，我们现在整体+1，那么不合法的数只会变成 $n+1$

而我们在上面保证数两两不同，所以我们可以直接让 $f(i,j)-=f(i-(n+1),j-1)$，相当于钦定一个数为 $n+1$

P4104 [HEOI2014] 平衡 （整数划分）

题目 https://www.luogu.com.cn/problem/P4104

考虑背包和整数划分dp的状态是一样的，但是整数划分的转移时 $O(1)$ 的，所以我们采用整数划分更优。

整数划分本质也是一种背包。

序列存在排列类dp

设 $f(i,j)$ 表示前 $i$ 个数有 $j$ 个不同的，然后枚举下一个是否相同：

• 不相同，直接转移到 $f(i+1,j+1)$，乘个组合数的转移系数
• 相同，转移到 $f(i+1,k)$，显然可以部分和优化掉

1014D. 牛仔（存在类dp+计数）

题目 http://47.92.197.167:5283/contest/412/problem/4

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133833513

对于 $A$，我们不关心其具体的值，只关心哪些位置相同。

对于 $A$ 互不相同的情况，我们直接计算计算牛仔序列的数量，然后中间记录 $A$ 的数量即可。

对于 $A$ 有相同的数的情况，有两种情况 ：

对于这种情况，我们两边分别计算然后乘起来即可

对于这种情况，我不会，但数据没卡

本质子序列个数dp

https://blog.csdn.net/zhangtingxiqwq/article/details/133885848

$f_i$ 设为 $i$ 结尾的方案数

假设每次遇到 $k$

$f_k=\sum f_i+1$

之前的所有情况和空集都可以接 $k$

本质01子序列个数的dp

https://blog.csdn.net/zhangtingxiqwq/article/details/133885358

设 $g$ 为本质不同方案，$f_{0/1}$ 为以0/1结尾本质不同子序列的方案。假设遇到数字 $i$

$$\begin{gathered} f_i^{\prime }=g \\ {g}^{\prime }=2g-f_i \end{gathered}$$

写成这个形式可以方便我们用矩阵做些奇奇怪怪的操作

状态设计

对于状态很难设计的问题，可以考虑几个方向：

1. 判定转状态
2. 贪心转状态
3. 答案与状态互换

判定转状态

ZR23NOIPD6B（操作转状态）

典型的一道最优决策类问题。相当于题目中的各种操作对应其相应代价。

发现球有两种可能：单个被染 / 整体被染。单个被染显然很好统计。对于整体被染的情况，难统计的交换的代价。考虑钦定哪些被染。我们按 $k$ 分组，每组内部就是个士兵站队问题，全部都贪心往中间站，这样子就很好统计交换的代价了。

因此 $f(i,j)$ 表示前 $i$ 个中有 $j$ 个整体染。转移时对于整体被染的情况，我们就可以很好地统计交换的贡献了。所以我们本质是一种判定转状态。

贪心转状态

对于贪心转dp类题目，我们首先是先对朴素情况进行一波贪心。

贪心转dp很经典的一种应用是博弈论+dp。

AGC022E Median Replace

题目：https://www.luogu.com.cn/problem/AT_agc022_e

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132152603

先贪心一波，000变0，001和011同时消去01。因此0的个数不超过两个。

假如我们维护消掉过程中的栈，必然是下1上0。我们维护堆顶是0个数不超过2。进入1，如果有0，就消掉0。所以栈底1的个数是不减的。所以我们维护1的个数最多为2即可。

答案与状态互换

CF1175E Minimal Segment Cover

题目：https://www.luogu.com.cn/problem/CF1175E

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132571504

按照正常套路 $d{p}_i$ 为到达 $i$ （限制）最少多少条（答案），其实可以转化为 $d{p}_i$ 用 $i$ 条（限制）最远可以到达哪里（答案）

我们设 $dp(i,j)$ 表示从 $i$ 开始用 $j$ 条线段最远到哪里

ICPC2021 Asia沈阳区域赛G（扩展dp状态）

题目 https://vjudge.net/contest/593228#problem/I

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134379201

朴素思路是 $dp[s][i]$ 现在还有 $s$ 的没填，从 $i$ 位置开始，最后的串，通过记忆化搜索来减少状态，但是还是过不了。

我们考虑继续扩展dp状态存的东西。$dp[s]$ 表示 $s$ 已填，串的字典序最大和endposs的最小位置。然后 $s$ 的补集必须在后面全部出现，因此我们就有一个右边界限制。假设我们枚举最后一个字符是 $c$，左边界就是 $dp[s-c].endposs$

dp优化

单调队列 / 单调栈优化

[IOI2000] 邮局 加强版 （二分单调队列）

题目：https://www.luogu.com.cn/problem/P6246

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132522515

使用二分队列的前提是满足决策单调性，但又不能双指针。

若 $d{p}_i$ 由 $j$ 转移，则 $d{p}_{i+1}$ 转移点 $k$ 满足 $k\ge j$

为什么不能双指针：因为我们不能保证 $[j+1,k-1]$ 中的决策的一定比 $j$ 优！

假设我们前 $i$ 个已经确定，后面未确定的决策点我们可以拿单调队列维护后面的决策点连续段。

当加入新决策点 $i+1$ 时，必然是先pop掉尾部一些区间，然后再和当前最末尾的一个共享一个区间。而找分界点我们采用的是二分。

四边形不等式优化

https://blog.csdn.net/zhangtingxiqwq/article/details/132134968

用于优化前 $i$ 个放 $j$ 个，决策点 $k$ 的枚举范围。

dp顺序为斜着dp。也就是说和差值有关。比如我们现在枚举 $op(i,j)$，我们可以求出其由 $op(i,j-1)$，那么根据差值分析，另一个范围决策点应该是 $op(i+1,j)$

[IOI2000] 邮局

题目：https://www.luogu.com.cn/problem/P4767

• 由 $op(i,j-1)$ 推到 $op(i,j)$，也就是距离相同，放的邮局可以更多，那么邮局肯定更“紧凑”，所以最后一个邮局肯定不会往前走。因此 $op(i,j)\ge op(i,j-1)$
• 由 $op(i+1,j)$ 推到 $op(i,j)$，也就是邮局数量相同，但距离更长，那么邮局应该更“疏松”，所以最后一个邮局肯定不会往后走。因此 $op(i,j)\le op(i+1,j)$

综上，$op(i,j-1)\le op(i,j)\le op(i+1,j)$

wqs二分

https://blog.csdn.net/zhangtingxiqwq/article/details/132522464

对于 $i$ 个数划分成 $j$ 段的dp，如果随着段数变化，结果的变化量满足凸性，那么我们就可以二分斜率，也就是选一段的代价，使得在这种情况下恰好选择 $j$ 段

[IOI2000] 邮局 加强版

题目：https://www.luogu.com.cn/problem/P6246

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132522515

发现是前 $i$ 个分成 $j$ 段的问题，同时我们容易 $d{p}_{i,j}$，考虑直接把 $j$ wqs掉。

P9338 [JOISC 2023 Day3] Chorus （wqs二分+斜率优化）

题目 https://www.luogu.com.cn/problem/P9338

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133955885

考虑暴力前 $i$ 个分 $j$ 段 $f_{i,k}=f_{j-1,k-1}+g_{j,i}$，$O(n^3)$

然后划分段数，段数显然越多越优，那么就上wqs二分，$O(n^2\log n)$

然后我们发现 $g$ 可以拆，拆完之后拿斜率dp优化即可。$O(n\log n)$

倍增优化

使用条件：

1. 答案具有可合并性
2. 针对询问而做的dp

CF1175E Minimal Segment Cover

题目：https://www.luogu.com.cn/problem/CF1175E

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132571504

我们设 $dp(i,j)$ 表示从 $i$ 开始用 $j$ 条线段最远到哪里

我们可以先倍增出 $dp(i,(1,2,\dots 2^{k-1},2^k))$ 的答案，询问的时候同样倍增来扩展

值域分块优化dp

0922D. 发怒 (fn)（乘积类）

题目 http://cplusoj.com/d/senior/p/SS230922D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133217931

如果我们直接维护 $dp[x][i]$，$i$ 表示值域，复杂度过大。

注意到我们是求积，而且有上界限制，我们在 $\le B$ 的 $i$ 的意义同上，$>B$ 的时候 $i$ 代表还可以最多选 $i$。

斜率优化dp

https://blog.csdn.net/zhangtingxiqwq/article/details/133955843

$f_i=\min (a_j-j\times i)$

考虑变成点对 $(j,a_j)$，则 $f_i=Y_j-X_{j}i$

令 $i=k,f_i=b$，得 $b=Y_j-X_{j}k$，即 $Y_j=X_{j}k+b$

我们希望 $b$ 尽量小，也就是截距尽可能小，即下图红色部分

对于点对，我们维护凸壳

可以发现，在第一个切的地方我们可以取截距最小

维护凸壳采用的是单调队列，我们维护两点之间斜率递增

如果新加入的点会使斜率递减，则把队尾的点pop掉

然后我们就可以二分 / 决策单调性了

P9338 [JOISC 2023 Day3] Chorus （wqs二分+斜率优化）

见wqs部分

dp转成其他东西

dp转矩阵

很常见

dp转自动机

1017D. 字符替换（replace）

题目 http://cplusoj.com/d/senior/p/SS231017D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133894734

根据求本质不同子序列的套路，我们发现每次就是在交换 $g$ 和 $f_i$ 的奇偶性，而本质不同的 $f$ 只有4种，因此我们可以基于每个 $f$ 建自动机，每个点，在任意一个串在自动机1上跑就可以求出本质不同子序列个数。

现在我们要查询一个串的所有子串。

此时我们可以记录一个 $2^4$，表示自动机1上每个点目前有多少个后缀（只需要记录奇偶性），再多加一个状态表示之前其他所有子串的奇偶性。

（注意这一步我们只需要记录所有后缀，因为如果不是后缀不会对后面产生影响）

然后就可以直接转移了。但我们发现这样子也就 $2^5=32$ 个点，我们可以又可以建出一个新的自动机。

正解是自动机+猫树分治，但我不会。

数据结构/ds

线段树

CF1371F Raging Thunder（线段树维护信息）

题目 https://www.luogu.com.cn/problem/CF1371F

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133745577

我们在线段树上维护正反的信息。对于某个方面，维护左右 > < 两个方向的信息。merge时大分类讨论即可。注意多对拍。

0912D. 聚会 （线段树维护dp）

题目：http://cplusoj.com/d/senior/p/SS230912D?tid=64ffe834f5f3679386f2da4b

显然左右可以分开考虑

考虑 $f_i$ 表示把一条消息传给右边的最小操作次数。我们按左端点排序，则 $f_i=min(f_j+1)$，满足区间 $i,j$ 有交，这个部分拿线段树维护。$g_i$ 同理。

但是区间会有包含关系，那么对于这个区间来说，如果直接传给大区间，可以使步数-1。传给哪个区间，显然是左端点最左和右端点最右的区间。

ZR23ABDay7矩形（动态信息维护系数）

题目：http://zhengruioi.com/problem/2612

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132255084

我们现在要动态维护笛卡尔树，但其实我们发现计算某个点贡献的时候左边是定了的，不确定的其实是右边，大致可以表示成 $l(n-i+1)$ （对于 $f$），而这又可以变成一个 $kn+b$ 的形式。

（当然 $f$ 也可能是个常数，我们令 $k=0$ 即可。至于什么时候变成常数，可以拿个单调队列维护）

由于我们进行了分治，现在相当于要动态维护 $\sum (k1n+b1)(k2m+b2)$（单点修改，全局拿 $n,m$ 查询）

我们可以拆开，发现一定可以表示成 $anm+bn+cm+d$ 的形式，我们分别维护 $a,b,c,d$ 即可。

0920D 后缀数组 suffix （线段树维护矩阵）

题目 http://cplusoj.com/d/senior/p/SS230920D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133100771

考虑相邻两个位置的偏序关系是由 $cm{p}_i,cm{p}_{i+1}$ 决定的，我们易列出dp式子。

由于涉及区间修改，我们可以写成矩阵形式，然后我们直接丢线段树上维护。

对于flip操作我们只需要提前记录这个区间反转后的记过。然后写好push_up即可。

对于reverse操作，那就把线段树变成平衡树，但我没打。

CF573D Bear and Cavalry （线段树维护dp矩阵）

题目 https://www.luogu.com.cn/problem/CF573D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133437456

我们按 $h$ 和 $w$ 排序打表得最多跨3。因此我们 $d{p}_i$ 就可以由 $i-1,i-2,i-3$，这易写成矩阵形式。（矩阵应该为max+矩阵）

由于矩阵具有结合律，我们直接拿线段树维护即可。

CF407E k-d-sequence （用单调队列维护min/max——把区间覆盖转区间加）

题目 https://www.luogu.com.cn/problem/CF407E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133749252

在 $l$ 定的时候，我们肯定能推出一个合法 $r$ 满足，$m{x}_r-m{n}_r-rd\le c$。

正常用线段树维护 $\min /\max$ 我们采用的是区间覆盖+tag，但现在涉及±，我们就不能用区间覆盖实现了。

考虑 $l$ 从大往小扫描线，$\min /\max$ 值我们可以采用单调栈维护。既然如此，我们在单调栈进出的过程变成区间加减即可。

CF403E Two Rooted Trees （线段树维护df序+势能均摊类）

题目 https://www.luogu.com.cn/problem/CF403E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134002988

场上想对于一棵树的某个子树把所有向外边全部删掉

变成dfn序一个在子树区间，一个不在的问题

易发现这个问题可以用线段树维护

在一个点在其dfn序加入另一个点，维护区间另一个点dfn序的最大和最小值

如果不在询问区间里，直接递归

易证明均摊是 $O(n\log n)$

树状数组

0919C 休息运动 run （分析性质题）

题目 http://cplusoj.com/d/senior/p/SS230919C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133047414

最快很显然，对于最慢的情况我们显然先在最左和最右各放置一个。

然后放置现在满足对称性，这样子对 $i$ 没影响，对其他更优。

然后就没必要放了，因为再放会使包括 $i$ 在内的点更优，但不会使得一些点更更更优，甚至还不变，导致答案更劣。

所以现在对每个点的附加就是一段段折线拼起来，拿个树状数组维护即可。

分块

1004A. 漂亮大厨 （涉及块内排序——散块排序）

题目 http://cplusoj.com/d/senior/p/SS231004A

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133560662

发现涉及到值域问题，我们考虑分块。如果块内元素已经有序，我们可以很容易求。

发现整体加不会影响块内元素顺序，所以我们只需要暴力循环小块即可，

离线

离线是解决ds问题的重要工具。

扫描线类

二维数点问题

二维数点问题是经典的扫描线+数据结构问题。

首先我们可以先扫描线，然后转成前缀和，那样子就可以把 $x$ 轴的限制去掉。

对于 $y$ 轴就是个一维问题，任意数据结构都可以维护。

P1502 窗口的星星 （平面转点）

题目 https://www.luogu.com.cn/problem/P1502

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133124669

发现正常扫描线很难维护恰好大小为 $W$ 的区间

反过来，我们对于每个点求出合法左上角的二维区间。

然后扫描线看最多覆盖的位置即可。

0926D. 隐形飞机(hide) （点转区间）

题目 http://cplusoj.com/d/senior/p/SS230926D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133309861

首先先扫描线，把右端点的限制去掉。

我们发现题目问的是恰好覆盖到 $u_i$，我们考虑转化为 $[u_i,v_i]$ 内所有点在被覆盖的条件下左端点最右都 $\ge u_i$ 即可。

这样子就可以很方便用线段树维护了。

CF1887D Split（枚举最大值+二维数点）

题目 https://www.luogu.com.cn/problem/CF1887D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133996658

考虑左区间最大值定的时候，右区间可取范围是确定的。

因此我们考虑从大往小加入数，枚举每个数作为左区间的范围，因此我们可以求出左区间的范围。然后右边连续一段就是右区间的范围。

然后变成一个二维数点问题，随便用分治或线段树维护即可。

ZR23BDay3 rdexq（离线+数论分块）

题目：http://zhengruioi.com/problem/2609

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132178041

首先数论分块，然后操作离线。我们按 $r$ 扫描线，找出满足条件的最左 $l$。对于每个 $a_i$，我们把所有满足 $a_i/a_j=x$ 最靠近的 $j$ （包括左右）都找出来，然后随便拿个东西维护即可。

CF1864F Exotic Queries （单调栈+树状数组）

题目 https://www.luogu.com.cn/problem/CF1864F

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132631673

已经忘记自己当时的做法了… 这里写的做法是口的

先离线。然后我们考虑 $a_i$ 什么时候可以省一步。当存在 $j$ 满足 $a_j=a_i$ 且 $a_k\ge a_i,k\in [j,i]$。

显然这个东西我们离线后可以拿单调栈维护，然后左端点在 $[j+1,i]$ 的做个区间加即可

1025D. 树上的数 （树上单次形态改变——维护重儿子与次重儿子）

题目 http://cplusoj.com/d/senior/p/SS231025D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134039125

首先答案为 $\sum w[x]-w[son[x]]$，$x$ 非儿子

我们肯定要考虑离线。对于祖先的变化有两种情况：

1. 重儿子不变
2. 重儿子改变

我们拿个ds维护差值即可

时间戳类

操作离线，逐个遍历点，维护每个时间戳的值

CF383C Propagating tree

题目：https://www.luogu.com.cn/problem/CF383C

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132471723

直接离线，把所有操作和询问挂到点上，拿个时间线段树，支持后缀加、单点查询操作即可。

RMQ

±1 RMQ

相邻之间相差恰好为1。

考虑分块

令 $B=\frac{{\log }_{2}n}{2}$，按 $B$ 分块

使用ST表处理大块间的 RMQ 问题

对于一个块内的 RMQ 问题，由于差分数组 $2^{b-1}$ 种，可以预处理出所有情况下的最值位置

void pre_ST() {
	int i, j, k, l; 
	b=(int)(ceil(log2(top)/2)); c=top/b; 
	Log2[1]=0; 
	for(i=2; i<=top; ++i) Log2[i]=Log2[i>>1]+1; 
	for(i=0; i<c; ++i) {
		Mn[i][0]=T[a[i*b]]; 
		for(j=1; j<b; ++j) 
			Mn[i][0]=max(Mn[i][0], T[a[i*b+j]]); 
	}
	for(k=l=1; l<c; ++k, l<<=1)
		for(i=0, j=l; i+(l<<1)-1<top; ++i, ++j) {
			Mn[i][k]=max(Mn[i][k-1], Mn[j][k-1]); 
		}
}

void pre_small() {
	int i, j, s; 
	for(i=0; i<=c; ++i) {
		for(j=1; j<b && i*b+j<top; ++j)
			if(T[a[i*b+j]].dep<T[a[i*b+j-1]].dep)
				Dif[i]|=(1<<j-1); 
	}
	for(s=0; s<(1<<b-1); ++s) {
		int v=0, mx=0; Pos[s]=0; 
		for(i=1; i<b; ++i) {
			if(s&(1<<i-1)) --v; 
			else ++v; 
			if(v<mx) {
				mx=v; Pos[s]=i; 
			}
		}	
	}
}

O(n)RMQ四毛子

ST表

1019A. 草莓列车(train) （ST表倒序释放）

题目 http://cplusoj.com/d/senior/p/SS231019A

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133926195

发现有一堆操作，但只有最后的查询。

我们可以在ST表对应区间打上标记，最后做一次释放即可。

复杂度 $O(nlogn+m)$

扫描线

平面+扫描线

题目：https://www.luogu.com.cn/problem/P5490

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132135063

思想：按其中 $y$ 排序，线段树维护 $x$ 轴的内容（维护一维上的长度并）。

每个矩形相当于有上边和下边，一个加一个减。

线段树合并

https://blog.csdn.net/zhangtingxiqwq/article/details/132135188

对于树上每个点，我们维护其线段树的时候，采用的方法是动态开点。

对于两棵线段树进行合并的时候，对于某个节点，如果两人都要，则递归下去，否则直接把有的挂在上面。复杂度最劣为小的线段树的大小。

NOD2207B 奇怪的树

题目：http://cplusoj.com/d/senior/p/NOD2207B

板子题。我们希望每个点装的点尽量多，肯定是从小往大装即可。如果我们能用线段树维护其子树内每个点的重量，我们只需要在线段树上二分即可。

而维护每个点的重量我们直接线段树合并即可。

珂朵莉树

CF1725K Kingdom of Criticism （珂朵莉树维护值域+并查集）

题目 https://www.luogu.com.cn/problem/CF1725K

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133607729

发现区间操作只有值域覆盖，所以我们对值域用珂朵莉树维护。

但是题目中还有单点操作，我们发现区间覆盖这个过程也会形成一个树形结构，所以我们就可以用并查集维护。珂朵莉树我们记录的值其中一个就表示当前的fa即可。

然后每次单点修改，它可能是其他的根，所以我们直接建个新点即可。

1018B. 补天 （非连续段需独立维护——使用set）

题目 http://cplusoj.com/d/senior/p/SS231018B

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133914164

同一个连续段可以拿线段树维护，但不同连续段之间要独立计算，那我们直接拿set维护连续段。

拿走时删掉线段树对应区间贡献，加入时加上线段树对应区间贡献。

李超线段树

构造

https://blog.csdn.net/zhangtingxiqwq/article/details/132217504

以上图为例，我们加入 $u$ 的时候，先在mid询问，可以得到 $u$ 是否完全覆盖其中一个区间。如果完全覆盖，就在 $v>u$ 的区间递归下区，否则在 $u>v$ 的区间覆盖下去。

用途

1. 维护线段覆盖问题
2. 维护一次函数
3. 维护斜率、维护凸包

CF1303G Sum of Prefix Sums （点分治+李超线段树维护一次函数）

题目：https://www.luogu.com.cn/problem/CF1303G

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132219909

首先询问两点之间，我们先上点分治。

考虑现在我们就是要合并两条道根的链。我们假设已知两条链的前缀和，那么新增的贡献则为 链1的末项×链2的长度。我们考虑用链2询问满足条件最大链1。

链1本身答案我们设为 $b$，链1末项我们设为 $k$，链2长度设为 $x$，则其贡献就是 $y=kx+b$，这是个一次函数，拿李超线段树维护即可。

zkw线段树

https://blog.csdn.net/zhangtingxiqwq/article/details/132177887

维护一棵满二叉树，然后我们就可以方便跳到叶子节点了。

以单点修改，区间取min为例：

zkw线段树的精髓其实是我们把开区间变成闭区间，这个方法在广义线段树类题目中广泛应用。

线段树分治

题目：https://www.luogu.com.cn/problem/P5787

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132126153

核心：离线 + 时间线段树

把每一个操作拆成 $\log$ 个操作，对应线段树上 $\log$ 个区间。

我们在线段树递归过程中，每一层维护当层的黑白染色结果。然后传给儿子，回溯时恢复为刚刚的黑白染色结果。

和分治维护背包类问题很像。

树套树

https://blog.csdn.net/zhangtingxiqwq/article/details/132501426

树状数组套权值线段树，实现过程类似主席树，采用动态开点实现

左偏树\可并堆

https://blog.csdn.net/zhangtingxiqwq/article/details/132507434

维护满二叉树的堆，合并 $x,y$ 时我们以小的为根，然后另一个递归到右子树里。满足任何时候都要左子树的最大深度大于右子树。

兔队线段树

本质：线段树上每层信息维护的时候通过递归进去维护。

核心思想：分治。对于每个分治区间我们只关心这个区间的结果。

P4198 楼房重建

题目：https://www.luogu.com.cn/problem/P4198

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132126096

先令 $p_i=\frac{y}{x}$，变成了斜率递增问题。

对于每个分治区间，左区间我们直接继承（因为必然可以全部看到），右区间我们递归进入。对于merge时的左右区间，如果左区间max可以被看到，我们就递归左区间，右区间我们可以直接求。否则我们递归右区间即可。

CCPC2023深圳K（兔队线段树维护哈希值判断序列同构）

题目 https://vjudge.net/contest/594134#problem/K

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134372798

如果两个序列的非严格递增后缀子序列同构，则同构。我们可以用哈希判同构，兔队线段树维护即可。

树上问题

多考虑dfn序！！！！

直径

和直径相关的题目是树上问题的热门

CF1192B Dynamic Diameter （动态维护直径）

题目：https://www.luogu.com.cn/problem/CF1192B

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132566345

一种不常见维护直径的方法：

$$\underset{(u,v)}{\max }(de{p}_u+de{p}_v-2\times de{p}_{lca(u,v)})$$

为了方便维护lca，我们可以转欧拉环游序。任意 $u,v$ 中必有 $lca(u,v)$ ，而且 $lca(u,v)$ 必然为任意 $u,v$ 中最浅的点

然后线段树维护即可

具体地，我们需要维护 $2dep(l)-dep(\text{线段树后缀min})$ 的最大值。

CF842E Nikita and game（树上所有直径的交集必然为一个连续段）

题目 https://www.luogu.com.cn/problem/CF842E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133280849

由于树上所有直径的交集必然为一个连续段，这个连续段就把直径的端点分成两部分，我们分别分别维护两部分即可。

我们对于新加入的点分别对两个点集求距离，如果长度恰好等于直径，就把它加入对应点集即可。如果长度大于直径就说明可以更新直径，而它自己就是一个独立的新点集。

但这样子过不了。对拍可以发现，另一个点集里的点不能够直接扔了，它可以加入另一个点集里。

CF1725J Journey（树上传送类）

题目 https://www.luogu.com.cn/problem/CF1725J

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133622359

显然一开始每条边都至少要走2遍。

任意地方开始，任意地方结束，可以让我们少走一条链。传送一次，也可以让我们少走一条链。但是这两天链不能交。

我们通过换根维护这两天链即可。需要注意到是，两天链可以交于一点，我们只需要对一个点求向外的4条链即可。

树上贪心

0909T1 数据恢复 data（贪心上树 + 决策唯一 + 树上缩点）

题目 http://www.accoders.com/problem.php?cid=4501&pid=0

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132795053

不考虑上树，就是个经典的贪心，也就是按 $b/a$ 排序。

丢树上，要求父亲必须比儿子先选，也就是多了一种限制条件。

但此时先从全局出发，对于某个节点若其 $b/a$ 为全局最大，那么选完父亲后必须选他，因为选择走其他地方必然没有走这里更优。

然后此时对于这个父亲节点，他现在的决策唯一

然后我们就可以把这个点和父亲节点缩在一起，继续做上述过程。

CF444E DZY Loves Planting （二分+max匹配）

题目 https://www.luogu.com.cn/problem/CF444E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133138502

考虑二分。然后对于每个点 $i$ 肯定会有一堆点合法，很难搞。

我们考虑只保留大于等于 $mid$ 的边，那么每个点只要和非自己连通块的点匹配即可。

然后就是个典了，只要满足 $w\ge \sum x_j$ 即可（其实就是Hall定理）

然后发现二分也不用了，并查集即可

P8341 [AHOI2022] 回忆 （树上匹配类贪心）

题目 https://www.luogu.com.cn/problem/P8341

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133780272

首先一棵子树内有一些完成匹配的链，我们直接让其两两匹配即可，因为在子树内匹配一定比在子树外优。（因为我们可以在外面拆掉子树内的匹配，但我们不能在外面再匹配子树里的）

然后假如向上有很多找祖先的，我们只需要保留一条即可。

我们记 $a,b,p$ 分别代表完成匹配，未完成匹配，新增的完成匹配。对于一个新的询问链，我们优先看是否有满足条件的 $p$，如果有直接更新top即可。如果没有我们肯定是优先用 $b$ 的，如果还没有我们就只能拆 $a$ 了，如果还不行只能新建 $p$ 了。

考虑合并子树。我们优先把 $b$ 全部匹配，如果还有剩我们拆 $a$ 即可。

细节有点多，多对拍。

1031A. 染色游戏 （维护子树贡献+类树形dp）

题目 http://cplusoj.com/d/senior/p/SS231031A

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134170718

可以发现从上面打下来，我们有两种对策：

1. 直接引一条上来
2. 下面每条分别对付

我们直接按照这种方法维护一个类似树形dp的东西就行了

树上启发式合并

CCPC 2020长春站F（拆完+dfn序优化枚举）

题目 https://vjudge.net/contest/587311#problem/C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133802611

拆完后变树上启发式合并板子，但是直接做会被卡常。

但考虑枚举子树的过程必然是dfn序的连续段，所以我们直接枚举dfn序连续段即可。

CCPC 2020长春站K（并查集启发式合并+枚举因数优化）

题目 https://vjudge.net/contest/587311#problem/E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133807724

打表可得当 $x$ 定的时候 $y$ 很小，所以我们就直接用类似并查集的启发式合并即可，用小的查询大的。

预处理的时候要先枚举 $gcd$，再枚举 $x$，这样子可以做到两只log。

点分治

题目：https://www.luogu.com.cn/problem/P3806

题解： https://blog.csdn.net/zhangtingxiqwq/article/details/132217048

1. 用一遍dfs找出当前分治树的重心，记为根节点
2. 从根节点通过各种方法维护跨根节点的信息
3. 每个子树分别点分治dfz下去

对于询问两点之间的问题，我们都可以考虑用点分治解决。

CF1303G Sum of Prefix Sums

询问两点之间的关系，之间点分治，后续见李超线段树。

[JOISC2020] 首都 （钦定类+颜色类）

题目：https://www.luogu.com.cn/problem/P7215

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132221132

题目求使一个颜色为一个连通块的最小合并次数。

考场上不一定能想到点分治，但对于具有后效性的连通块问题如果我们往点分治想会有意想不到的结果。

假设我们点分治，那么就是钦定根节点必选。然后转化为朴素树上问题，不断维护新颜色即可。

0922D. 发怒 (fn)（点分治+连通块dp）

题目 http://cplusoj.com/d/senior/p/SS230922D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133217931

树上连通块，显然点分治。

对于钦定根的连通块问题，除了树形dp，我们还可以按照dfn序倒序dp。

具体的，对于当前点 $i$（注意这里都是指dfn序），我们可以钦定 $i$ 是否选

如果 $i$ 选，就由 $i+1$，也就是 $i$ 的第一个儿子转移过来（因为只有他选他子树才可能被选）

如果 $i$ 不选，就由 $i+w_i$ 转移过来，因为他的儿子必然不会被选

至于 $i$ 和 $i+w_i$ 同时选的情况，我们在 $i+1$ 那里已经算了

对于 $i$ 和 $i+w_i$ 是否连通的问题，当他们的lca都被选时，则他们必然也被选，这里一定会在他们祖先那里被算到

树链剖分

0914D. 校门外歪脖树上的鸽子pigeons（广义线段树上树链剖分）

题目 http://cplusoj.com/d/senior/p/SS230914D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132891386

对于广义线段树的题目，我们一般来说维护的方法都是转成类zkw线段树

发现现在变成里链加和链查询，我们对广义线段树树剖即可。

长剖与树上贪心

1004D. 漂亮轰炸 （长剖后反悔贪心）

题目 http://cplusoj.com/d/senior/p/SS231004D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133575747

假如没有 $a_i$ 的限制，我们对树进行长剖，然后选前 $2k-1$ 大的链即可。

考虑现在有个 $a_i$，我们需要反悔掉，发现只有两种情况：

1. 舍弃第 $2k-1$ 长的链。
2. 向上找第一条链，把它掰过来

找第一条链直接倍增跳就行

虚树

1008D. 虚树 （长剖贪心+ST表维护虚树+虚树合并）

题目 http://cplusoj.com/d/senior/p/SS231008D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133690843

选 $k$ 个点，经典的长剖贪心套路，其实就是选前 $2k-1$ 长的链。

我们可以用ST表预处理每个块内的虚树，然后查询的时候把虚树合并即可。

类似直径，长剖也具有合并性。

圆方树

void dfs(int x) {
	dfn[x]=low[x]=++tot; z.push(x); 
	for(int y : T[x]) {
		if(!dfn[y]) {
			dfs(y); 
			low[x]=min(low[x], low[y]); 
			if(low[y]==dfn[x]) {
				cun(x, ++num); 
				while(z.top()!=y) cun(z.top(), num), z.pop(); 
				cun(y, num); z.pop(); 
			}
		}
		else low[x]=min(low[x], dfn[y]); 
	}
}

易错点：

1. 不用记录父亲，因为普通一条边也可以作为边双的一部分
2. 由于求的是边双而不是点双，所以判断应为 low[y]==dfn[x]，表示 $y$ 最多可以返祖到 $x$

[ABC318G] Typical Path Problem （路径问题）

题目 https://www.luogu.com.cn/problem/AT_abc318_g

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132645934

对原图建圆方树后，任意两点间的简单路径必然为其树上路径上方点对应其边双的点。

然后判断A，C路径上的方点是否会有B

![在这里插入图片描述](https://img-blog.csdnimg.cn/3fd6fea507664b23bb7169b56b99414d.png

计数 / 数数

板子：https://www.luogu.com.cn/paste/6le701n6

线性求逆元

https://blog.csdn.net/zhangtingxiqwq/article/details/132650059

• 先暴力求出 $\frac{1}{n!}$
• 往回推出 $\frac{1}{i!}$
• $\frac{1}{i}=\frac{(i-1)!}{i!}$

杨辉三角

杨辉三角按列求和

https://blog.csdn.net/zhangtingxiqwq/article/details/133906909

直接暴力展开即可：

$$\sum _{i=0}^n\left(\genfrac{}{}{0ex}{}{i}{k}\right)=\left(\genfrac{}{}{0ex}{}{n+1}{k+1}\right)$$

$$\sum _{i=l}^r\left(\genfrac{}{}{0ex}{}{i}{k}\right)=\left(\genfrac{}{}{0ex}{}{r+1}{k+1}\right)-\left(\genfrac{}{}{0ex}{}{l}{k+1}\right)$$

杨辉三角按行求和（莫队法）

https://blog.csdn.net/zhangtingxiqwq/article/details/133559588

设 $S(n,m)={\sum }_{i=0}^m\left(\genfrac{}{}{0ex}{}{n}{i}\right)$，若求 $S(n,m+1)$，直接加上 $\left(\genfrac{}{}{0ex}{}{n}{m+1}\right)$ 即可。

假如推到 $S(n+1,m)$，我们直接丢到杨辉三角上暴力展开，发现除 $\left(\genfrac{}{}{0ex}{}{n}{m}\right)$ 外都有2倍贡献。因此 $S(n+1,m)=2S(n,m)-\left(\genfrac{}{}{0ex}{}{n}{m}\right)$

发现这个过程我们可以离线下来用莫队求。

拆贡献

ARC165E Random Isolation（按连通块拆贡献+枚举可跳过操作顺序）

题目 https://atcoder.jp/contests/arc165/tasks/arc165_e

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132971902

考虑拆贡献，一个有 $n$ 个点 $m$ 个相连点的连通块的贡献就是其存在概率。

考虑枚举可跳过的操作顺序，则前 $m$ 个点必然早于这 $n$ 个点，所以概率为 $\frac{n!m!}{(n+m)!}$

合法 $(n,m)$ 对的计算直接树形dp即可。

1006C. 数点（多次方问题考虑组合意义来拆贡献）

题目 http://cplusoj.com/d/senior/p/SS231006C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133621275

题目问 $|S{|}^3$，$|S|$ 表示选的点数。相当于在 $|S|$ 中选了3次，也就是选了3个可相同的点（需要注意的是，我们这样子钦定是考虑顺序的）。

因此我们可以分类讨论，用ds来维护。

以选3个不同的点为例，对于任意3个点，必然会对所有包含其的矩形产生贡献，所以只需要统计多少个矩形包含其即可，注意乘上全排列6.

arc163_d Sum of SCC（用划分法拆连通块贡献）

题目 https://atcoder.jp/contests/arc163/tasks/arc163_d

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132994501

首先竞赛图缩点成链，于是我们考虑枚举划分，划分成两个集合 $A，B$，只能有 $A\to B$，允许 $A$ 为空。那么划分方案数恰对应连通块数量。

于是 $dp(i,a,b)$ 表示已用 $i$ 条往前边，有 $a$ 个在 $A$ 里，$b$ 个在 $B$ 里的方案数。对于每个新点，我们枚举它被放到哪个集合里。它连向另一个集合的边方向是确定的，连向自己集合的边我们可以枚举有 $x$ 条返祖，然后乘个组合数即可。

斐波那契数列

[ARC122C] Calculator （正整数的斐波那契分解）

题目 https://www.luogu.com.cn/problem/AT_arc122_c

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134198490

任意一个正整数都可以用 $\log$ 个斐波那契数加起来。

而这时典型的斐波那契形式

排列与置换环

[ABC318Ex] Count Strong Test Cases （计数转概率）

题目 https://www.luogu.com.cn/problem/AT_abc318_h

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132650494

先转为概率，$f_i$ 表示 $i$ 个点两人都AC的概率，$g_i$ 表示恰好一个人AC的概率。

两个人都AC，只能为全部自环，$f_i=\frac{1}{i!}$

现在求 $g_n$。然后有个定理，$n$ 个点形成的图形，$n$ 所在的环的大小在 $[1,n]$ 内随机生成。（很好证明）

然后考虑枚举 $n$ 所在的环大小为 $i$，先考虑由 $f$ 推向 $g$ 的情况。剩下 $n-i$ 个点两个人都AC，所以为 $f_{n-i}$。那么当前这个环只能有一个人AC，所以环大小至少为2。

此时谁AC都可以，所以最小的那条边有两个选择，即 $\frac{2}{i}$。因此 $f\to g$ 的答案为：

$$g_n=\frac{{\sum }_{i=2}^n\frac{2}{i}{f}_{n-i}}{n}$$

现在考虑 $g\to g$ 的贡献。之后的贡献为 $g_{n-i}$。发现他已经保证了恰好一个人AC，而且已经确定了这个人是谁。那么当前这个环的选择唯一，但大小可以使1，因为即使两个人在这个环内同时AC也无所谓。

$$g_n=\frac{{\sum }_{i=1}^n\frac{1}{i}{g}_{n-i}}{n}$$

结合起来就是：

$$g_n=\frac{{\sum }_{i=1}^n(\frac{2}{i}{f}_{n-i}(i\ne 1)+\frac{1}{i}{g}_{n-i})}{n}$$

令 $a_i=\frac{2}{i}$ 且 $a_1=0$，$b_i=\frac{1}{i}$

然后上面就变成了：

$$g_n=\frac{{\sum }_{i=1}^n(a_i{f}_{n-i}+b_i{g}_{n-i})}{n}$$

前面NTT，后面是个分治NTT即可。

1024B. 排列 （组合计数+容斥）

题目 http://cplusoj.com/d/senior/p/SS231024B

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134013962

发现要么是环，要么是链。如果是链，我们缩成点即可。然而直接统计会有问题。

长为2的链如果成二元环不应该乘2，那么考虑容斥

$g(i)$ 表示至少有 $i$ 个二元环不被算错的方数，${\sum }_{i=0}^{k}g(i)(-1{)}^{k-i}$

$g(i)=\left(\genfrac{}{}{0ex}{}{k}{i}\right)(z+i)!2^i$

1006B. 冒泡排序趟数期望 （排列中每个数前比其大的数的个数）

题目 http://cplusoj.com/d/senior/p/SS231006B

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133611553

我们设 $inv[i]$ 代表位置 $i$ 前面比 $p_j$ 大的数个数，他有优良的性质：

• $inv[i]\in [0,i-1]$
• $inv$ 的所有排列恰好与所以原排列一一对应。因为从后往前求 $inv$ 一定可以唯一还原成一个排列

现在相当于求 $\max inv[i]=k$ 的排列个数，显然 $\le k$ 的位置可以随便填，后面的位置只要至少一个位置等于 $k$ 即可，其他的都必须满足 $<k$。我们可以用总方案减去所有位置都不合法的方案数。也就是 $k!((k+1{)}^{n-k}-k^{n-k})$

AT_wtf22Day1B Non-Overlapping Swaps （置换环+笛卡尔树）

题目 https://vj.imken.moe/problem/AtCoder-wtf22_day1_b

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133644610

数的交换，显然考虑置换环。我们显然不会对置换环进行合并，所以置换环只会分裂。因此每个置换环的操作次数为 $sze-1$。多出来的操作我们直接在所以置换环之间丢个 $[1,1]$，消去他们的互相影响。

对于一个置换环进行分裂成两个小环，这两个小环必然原先环的两个子区间。

我们要让相邻的操作不交，一个处理方式是对于一个位置，我们前后跳来跳去，也就是和位置的大小关系有关。

发现有大小关系+分裂子区间，很笛卡尔树，所以我们建一棵笛卡尔树，然后直接中序遍历即可。

但是我们发现根节点没有父亲，我们在破坏成链的时候，钦定最小值在开头即可。

容斥

ABC321G Electric Circuit（连通块拆贡献+状压+容斥）

题目 https://atcoder.jp/contests/abc321/tasks/abc321_g

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133266690

拆开统计每个连通块的贡献，显然可以直接状压。

对于统计块内连通，只需要减去不连通的情况，枚举子集容斥一下即可。

1007C. 数 (number) （恰好至少用乘除和差分互转）

题目 http://cplusoj.com/d/senior/p/SS231007C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133697910

求 $\gcd$ 的对应的乘积，我们可以设 $g(d)$ 表示 $\gcd$ 恰好为 $d$ 的乘积和，然后转成至少为 $f(d)$。$f$ 变成 $g$，可以莫反，也可以直接 $g(d)=\frac{f(d)}{{\prod }_{d|n,d\ne n}g(n)}$

考虑计算 $f(d)$，每个数的取值范围为 $[1,\frac{m}{d}]$，先计算好 $d$ 的贡献为 $d^{(\frac{m}{d}{)}^n}$，然后拆贡献算 $p^c$ 的贡献。

我们如果直接算还要考虑 $p^{c+1}$ 不在 $lcm$ 里面，所以我们可以算 $lcm$ 至少为 $p^c$ 的贡献，差分回去就行。

对于 $p^c$ 的贡献，只要其中一个是就行。因此我们可以用所有方案来减去 $p$ 的次幂大于等于 $c$ 的积。

二项式定理

枚举子集与二项式定理

https://blog.csdn.net/zhangtingxiqwq/article/details/133702110

$$\begin{array}{rl}\sum _{y\subseteq x}(-1{)}^{|y|}& =\sum _{i=0}^{|x|}\left(\genfrac{}{}{0ex}{}{|x|}{i}\right)(-1{)}^i\\ & =\sum _{i=0}^{|x|}\left(\genfrac{}{}{0ex}{}{|x|}{i}\right)(-1{)}^i{1}^{x-i}\\ & =(1+(-1){)}^{|x|}=0^{|x|}=0\end{array}$$

基环树计数

就是非排列的置换环，由于每个点出度为1，所以就变成了基环树了。

CF1863G Swaps

题目 https://www.luogu.com.cn/problem/CF1863G

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132696642

考虑交换的本质是什么。$i\to j\to k$，变成 $i\to k,j\to j$。所以每个点都可以从之前引一条边，总方案为 ${\prod }_v({\mathrm{in}}_v+1)$

同时又不合法和重复的：

所以总方案为：

$$\prod _{\text{cycles}}\left(\prod _{i=1}^k({\mathrm{in}}_{c_i}+1)-\sum _{i=1}^k{\mathrm{in}}_{c_i}\right)\cdot \prod _{\text{other }v}({\mathrm{in}}_v+1).$$

至于第二种情况会不会引更多下来。注意到我们的 $({\mathrm{in}}_v+1)$ 是在外面乘的，所以我们也考虑了这种情况

Prüfer / Prufer 序列

构造

https://blog.csdn.net/zhangtingxiqwq/article/details/132090250

从小到大枚举叶子节点（指度数为1的点），记录其父亲。

线性构造其实是对树进行拓扑排序，这里采用类似双指针的方法。假设 $nw$ 为当前点，且去掉后父亲节点向下度数为0

1. 若 $fa<p$，则 $nw=fa$
2. 否则直接从 $p$ 开始往后找，这个过程中要更新 $p$

本质上我们往前跳只会有 $fa$ 的情况。否则正常情况下我们只需要从 $p$ 开始横推即可

还原回去就是父亲找儿子。我们同样找第一个度数为0没父亲的点。如果这个父亲度数为0，我们加入的时候也是用上述方法进行

Cayley 公式

https://blog.csdn.net/zhangtingxiqwq/article/details/132832172

• $n$ 个点的无根生成树为 $n^{n-2}$

一个生成树和其prufer序列是唯一对应的

所有生成树和所有Prufer序列形成一个双射关系

而Prufer序列长度为 $n-2$，值域为 $n$，所以方案为 $n^{n-2}$

有度数限制的生成树计数

每个点有度数限制，我们可以先考虑枚举每个点的度数（也可以是Prufer 序列中的出现次数）

假设出现次数为 $a$，可以得出其生成树方案为 $\frac{n!}{\prod (a_i-1)!}$

0912A 圣诞树 （推式子+组合数化简+范德蒙德卷积）

题目 http://cplusoj.com/d/senior/p/SS230912A?tid=64ffe834f5f3679386f2da4b

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132839073

生成树方案：$\frac{n!}{\prod (a_i-1)!}$，然后后面会乘一堆组合数。但这些组合数和下面的阶乘进行变换也可以变成其他组合数，然后范德蒙德卷积即可。

范德蒙德卷积

$$\sum _{i=0}^k\left(\genfrac{}{}{0ex}{}{n}{i}\right)\left(\genfrac{}{}{0ex}{}{m}{k-i}\right)=\left(\genfrac{}{}{0ex}{}{n+m}{k}\right)$$

如果发现组合数下面都为 $+i$，我们可以考虑变位 $n-i$。然后加起来就消掉了（oiwiki中的4个推论都可以这样直接来）

范德蒙德卷积选数相同的合并：https://blog.csdn.net/zhangtingxiqwq/article/details/132863313

0912A 圣诞树

见prufer序列部分

Lucas定理

Lucas在与位运算有关的组合数中的应用

https://blog.csdn.net/zhangtingxiqwq/article/details/133176573

求 $\left(\genfrac{}{}{0ex}{}{n}{m}\right)\mathrm{mod}2$

根据 Lucas，有 $\left(\genfrac{}{}{0ex}{}{n\mathrm{mod}2}{m\mathrm{mod}2}\right)\left(\genfrac{}{}{0ex}{}{n/2}{m/2}\right)$

也就是 $\left(\genfrac{}{}{0ex}{}{n\&1}{m\&1}\right)\left(\genfrac{}{}{0ex}{}{n>>1}{m>>1}\right)$

假设结果为奇数，则任意 $\left(\genfrac{}{}{0ex}{}{n\&1}{m\&1}\right)$ 必须为1，则 $m\&1\subseteq n\&1$

每一位都满足，也就是 $n\&m=m$ 时为奇数

Spener定理

对于一个 $n$ 元集合 $S$，选出若干子集满足无包含关系，则最多选 $\left(\genfrac{}{}{0ex}{}{n}{\lfloor \frac{n}{2}\rfloor }\right)$ 个，每个的大小为 $\lfloor \frac{n}{2}\rfloor$

CF1257G Divisor Set （Spener定理+生成函数）

题目 https://www.luogu.com.cn/problem/CF1257G

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133270189

显然选 $\lfloor \frac{n}{2}\rfloor$ 个最优。但数之间会有重复，我们要计算选 $\lfloor \frac{n}{2}\rfloor$ 个的方案数，考虑把每个数写成生成函数形式，然后卷起来取 $x^{\lfloor \frac{n}{2}\rfloor }$ 的系数即可。

卷的过程要启发式合并。

莫比乌斯函数 / 反演

莫比乌斯函数的应用：

1. 式子化简
2. 容斥 / 反演

莫比乌斯函数的式子化简

划分质因子为两个不交集合的方案数

https://blog.csdn.net/zhangtingxiqwq/article/details/132355546

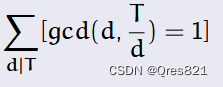
我们设 $T$ 的质因数集合大小为 $w(T)$，我们其实要求的是 $2^{w(T)}$

我们发现如果两个数的底数相同，指数不同，那么他们在同一个等价类里面，所以我们指数全部为0，也就是 $\mu (d)\ne 0$。

而所有的这些 $d$ 其实就是 $2^{w(T)}$ 中的一种选数方法，因此总方案数为：

μ^2的根号暴力计算方法

https://blog.csdn.net/zhangtingxiqwq/article/details/132386010

左边式子的本质就是 $n$ 以内有多少个数没有平方因子

然后我们枚举所有平方因子 $i^2$，包含它的有 $\frac{n}{i^2}$ 个，然后我们莫反一下即可

多项式

重所周知，NOIP 不考

FFT / NTT

• 傅里叶变换(FFT)笔记存档 https://blog.csdn.net/zhangtingxiqwq/article/details/132582930
• 多项式乘法（FFT） https://blog.csdn.net/zhangtingxiqwq/article/details/132588646
• FFT代码上的实现细节 https://blog.csdn.net/zhangtingxiqwq/article/details/132584208
• NTT总结 https://blog.csdn.net/zhangtingxiqwq/article/details/132591415

Gym - 104386G CLC Loves SQRT Technology (Hard Version) （组合数+2的幂次）

题目 https://vj.imken.moe/contest/579844#problem/I

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132866002

求 $\left(\genfrac{}{}{0ex}{}{n-j+i-1}{n-j}\right)2^{j-i-1}$

令 $a_i=\frac{2^{-i-1}}{(i-1)!},b_i=\frac{2^j}{(n-j)!}$，计算 $f_k={\sum }_{i+j=k}{a}_i{b}_j$

答案为 $\sum f_{k}k!$

多项式求逆

https://blog.csdn.net/zhangtingxiqwq/article/details/132612478

分治NTT/在线卷积

https://blog.csdn.net/zhangtingxiqwq/article/details/132670095

反射容斥

Loj #6738. 王的象棋世界（一维反射容斥）

题目 https://loj.ac/p/6738

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132978606

我们可以对棋盘进行翻倍，构造循环棋盘，把走出棋盘的情况将军饮马过去：

多项式快速幂计算即可

P9366 [ICPC2022 Xi’an R] Square Grid （二维反射容斥+曼哈顿距离转切比雪夫距离）

题目 https://www.luogu.com.cn/problem/P9366

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133707260

首先我们可以先将军饮马：

对于二维问题，我们的解法应该是考虑转成一维。一个好方法是我们求曼哈顿距离，我们转切比雪夫距离即可。相当于独立出来，两个维度分别要走多少步。（其实就是斜着走）

由于是正方形棋盘，所以不会互相影响。

我们转成一维后相当于是一维从 $x\to y$ 用 $t$ 步。我们可以先用多项式快速幂预处理（注意是循环数组），求出 $0\to d$ 用 $t$ 步的方案。

min-max容斥

https://blog.csdn.net/zhangtingxiqwq/article/details/133698526

设 $S,T$ 都是可重序列

$maxS={\sum }_{T⊊S}minT(-1{)}^{|T|-1}$

$minS={\sum }_{T⊊S}maxT(-1{)}^{|T|-1}$

用min-max容斥实现lcm与gcd互换

https://blog.csdn.net/zhangtingxiqwq/article/details/133698576

lcm本质是每个质因子质数取max，gcd是每个质因子质数取min

然后我们就可以直接套min-max容斥：

图论

生成树

1019B. 草莓路径(path) （树上选链和环）

题目 http://cplusoj.com/d/senior/p/SS231019B

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133932506

题目相当于在树上选一条链和一堆环。

我们考虑dfs生成树，链相当于是根节点开始的一条链，环相当于是每条返祖边所形成的环。

显然，每种链和环都可以出来。

二分图

常见性质

https://blog.csdn.net/zhangtingxiqwq/article/details/132076492

https://blog.csdn.net/zhangtingxiqwq/article/details/132077398

二分图中最小边覆盖=n-最大匹配

每条边可以覆盖1~2个点。显然最大匹配里的边都可以覆盖2个点。剩下每条边最多覆盖一个点。

匈牙利算法

https://blog.csdn.net/zhangtingxiqwq/article/details/132517702

左边的点轮流匹配，看是否能匹配成功。

对右边的点进行记录是否尝试过

然后有空就进，别人能退的就进

代码：https://atcoder.jp/contests/abc317/submissions/44984498

Hall 定理 / 霍尔定理

二分图存在完美匹配充要条件：

左部所有点集 $S$ 对应右边的 $N(S)$ 满足：$|S|\le |N(S)|$

[ABC317G] Rearranging（根据约束+Hall定理证明可行）

题目：https://www.luogu.com.cn/problem/AT_abc317_g

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132517757

考虑行向点连边，询问是否存在 $m$ 次完美匹配。

根据题目约束，我们可以用Hall 定理证明一定可以构造。因此跑 $m$ 次网络流来构造即可。

欧拉回路/路径

https://blog.csdn.net/zhangtingxiqwq/article/details/132082624

求欧拉回路的方法其实是套环

进入一个点的时候就去dfs下去，走的时候记录

void dfs(int x) {
	for(; t[x]<G[x].size(); ) {
		int y=G[x][t[x]]; ++t[x]; 
		dfs(y); 
	}
	z.push(x); 
}

1116D. 宿命（life） （图通过+欧拉路径判方案）

题目 http://cplusoj.com/d/senior/p/SS231116D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134444131

题目提示我们考虑相邻的数永远不会变，所以如果我们在相邻的数之间连边，$A$ 能变成 $B$ 的必要条件是两个图同构。

然后我们证明任意一条欧拉路径都可以由原序列做出。

我们按顺序考虑每条边，如果两个图同构，则要么同时为桥，要么同时不为桥。如果同时为桥，除非之前已经遍历完，不然不可能是欧拉路径。如果同时不为桥，必然存在一条边往外，因此我们就可以交换了。

2-SAT

对于或操作，我们建有向边，变成且操作。

比如：x1为真或x3为真，我们变成 x1为假则x3为真 和 x3为假则x1为真。

如果 x1为真 和 x1为假 在同一个强连通里，则不合法。

1019C. 草莓城市(city) （计算几何+2-sat）

题目 http://cplusoj.com/d/senior/p/SS231019C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133943270

我们这样子转化，则0/1必选一个，2/3必选一个，那么就变成一个2sat问题。

两三角形有交，则一个选，一个不能选

对角三角形一个选，一个不选。一个不选，一个选

三角形不合法，则选向不选连边，代表必须不选

哈密顿回路

https://blog.csdn.net/zhangtingxiqwq/article/details/132992984

哈密顿回路是一个经过所有节点恰好一次的回路。

竞赛图

有向完全图

性质

缩点后成链状，不是真正的链，只是类似链的偏序关系。

平面图欧拉定理

https://blog.csdn.net/zhangtingxiqwq/article/details/134062975

$V-E+P=B+1$

• $V$ ：点数
• $E$：边数
• $P$：面数（含外面）
• $B$：连通块数量

通过这个我们可以处理网格图中的连通块数量问题

上图中有7个点，8条边，3个面（包括外面），所以有 7-8+3=1+1 个连通块

1026B. 鬼渊

题目 http://cplusoj.com/d/senior/p/SS231026B

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134063018

考虑如何维护黑色连通块恰为1这个条件。我们可以直接运用平面图的欧拉公式。

对于“空腔”这个条件，我们可以先预处理，然后通过two-pointers+桶来实现

耳分解

https://blog.csdn.net/zhangtingxiqwq/article/details/132112802

对于无向图中的任意边双和有向图中的任意强联通都可以按照此方法构造：

1. S = { u } S=\{u\} S={u}
2. 每次找 $S$ 的两个元素 $u,v$（可相同），找一条不经过 $S$ 的路径，并把路劲上的所有点加入 $S$
   

可以拿来dp，来构造某种条件的边双。

常用的状态设计 $f(S)$，然后枚举 $T$ 为 $S$ 补集的子集。再枚举 $u,v\in S$。这种是 $O(3^n\times n^2)$。（每个点有3种状态：遍历完/遍历中/未遍历）

部分题目可以：$f(S,i,j)$ 当前在 $i$ 目标点为 $j$，然后转移可以枚举 $j$ 或者是不在 $S$ 中的点。$O(2^n{n}^2)$

双极定向

给无向图每条边定向后可以变成DAG，且 $s$ 为总起点，$t$ 为总终点。

双极定向有个优良性质：考虑其拓扑序为 $p$

则 $p_s,\dots ,p_i$ 和 $p_{i+1},\dots p_t$ 的子图都联通。

字符串

括号序列

括号序列不是传统的字符串算法，经常和dp、贪心等一起考

括号序列与问号的充要条件

https://blog.csdn.net/zhangtingxiqwq/article/details/132548658

判断 $str[l:r]$ 是否合法：

1. 把所有 ? 替换成 ‘(’，然后前缀和记为 $s$，满足任意时刻 $s_i\ge s_{l-1}$
2. 把所有 ? 替换成 ‘)’，然后后缀和记为 $t$，满足任意时刻 $t_i\ge t_{r+1}$

注意，这是一个充要条件（在 $r-l+1$ 为偶数的情况下）

AC自动机

https://blog.csdn.net/zhangtingxiqwq/article/details/132818609

性质

不带修，不支持合并。因此如果我们要修改AC自动机有两种做法：

1. 离线
2. 根号重构

查询一个串的子串（并不是所有，但我们只关心有用的）

任何一个串的子串都可以表示成他的一个前缀的后缀

他的前缀可以在Trie树上查询

后缀相当于其在fail树上的所有祖先

HDU - 4117 GRE Words（离线建AC自动机 + 线段树维护fail树）

题目 https://vjudge.net/contest/579844#problem/D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132804430

先离线建AC自动机。查询子串相当于询问祖先。

发现这不太好做，我们倒着做，就变成了查询子树。

然而还有时间戳这个限制，但我们可以拿个线段树维护（dfn序）。

HDU - 4787 GRE Words Revenge （根号重构AC自动机）

题目 https://vjudge.net/contest/579844#problem/E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132812068

我们维护两个AC自动机，分别是大AC自动机和小AC自动机。

小AC自动机每次重构，大AC自动机根号次重构。

Gym - 104542F Interesting String Problem（离线建AC自动机+Kruskal重构树+操作离线差分）

题目 https://vjudge.net/contest/579844#problem/F

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132818179

有了第一题的基础，我们考虑离线建AC自动机，然后拿个数据结构动态维护当前可行串。

然而有连边和询问连通块操作，考虑Kruskal重构树。每个操作相当于询问一个区间，考虑dfn序，就是一段连续一段区间。那么我们就可以考虑操作离线后差分即可。

回文自动机PAM

题目：https://www.luogu.com.cn/problem/P5496

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132136120

PAM的一个特点是回文串有两类，奇回文和偶回文。所以如果我们维护 $nxt$ 指针，奇只会对应到奇，偶也只会对应到偶。

PAM关键点：一个回文串的broder一定也是回文串，而且所有回文子串都可以用此方法构造

因此，我们可以通过维护最长border，也就是fail指针。

为了维护上述过程，我们要新建两个辅助点。分别为0点和-1（长度为-1，我们用1号点表示）点，分别代表奇回文的祖先和偶回文的祖先。显然nxt就是这棵两颗树。

考虑维护fail指针。 cc 匹配失败应该尝试匹配 c，所以我们要让 $fail[0]=1$（因为 cc 的父亲是 c，c 的fail为0，0直接接 c 变成偶回文了，所以我们要去更短的-1点）

我们应该匹配fail再加入点。在 ab 中，如果 b 先加入了，-1点会连向 b。而我们计算fail的时候就会是 b 为其broder了。（计算fail就是在计算broder，类似AC自动机的过程）

int find(int x) {
	while(s[i-len[x]-1]!=s[i]) x=fail[x]; 
	return x; 
}
fail[0]=1; len[1]=-1; lst=tot=1; 
for(i=1; i<=n; ++i) {
	c=s[i]; lst=find(lst); //找到以 s[i] 结尾的最长回文串
	if(!nxt[lst][c]) {
		u=++tot; 
		fail[u]=nxt[find(fail[lst])][c]; //找broder 
		nxt[lst][c]=u; 
		num[u]=num[fail[u]]+1; 
		len[u]=len[lst]+2; 
	}	
	u=nxt[lst][c]; 
	lst=u; las=num[u]; 
	printf("%lld ", las); 
}

后缀自动机SAM

https://blog.csdn.net/zhangtingxiqwq/article/details/132560666

每个点表示一个等价类，等价类里的串末尾出现位置集合一样。

如果 $nxt[p][c]$ 为空，我们就让其为 $u$，然后令 $p=fail[p]$，一直跳到一个不为空的地方，我们设跳到那个点为 $q$。

我们跳到的 $q$ 的长度（应该说前面的那些串并不能匹配当前串）不一定我们所希望的，因此我们需要拆成两个点 $q,cq$。

分类讨论 $fail$ 和 $nxt$ 的变化即可。

CF461E Appleman and a Game（SAM预处理+矩阵快速幂+贪心+二分）

题目 https://www.luogu.com.cn/problem/CF461E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133316261

这题丢到SAM上会好想很多。

考虑一个确定的串 $s$ 的最小操作次数。我们对 $t$ 建SAM，然后我们让 $s$ 在SAM上跑，如果没有后继节点就回到初始点，操作次数+1。易证明这个贪心是对的。

因此 $s$ 必然可以划分成一段段，每一段都是SAM上从根开始的一条链。同时满足下一段的开头不是上一段结尾的点的nxt。

因此我们可以预处理出 $G[a][b]$ 表示 $a$ 开头，下一个字符不能是 $b$ 的最短字符串长度。$G$ 显然可以在SAM上预处理出来。

我们考虑二分操作数。然后我们维护一个 $1\times 4$ 的矩阵 $f^k$，分别表示每种字母结尾（不含）用 $k$ 次操作的最短长度，$G$ 就是对应的转移矩阵。

后缀数组SA

https://blog.csdn.net/zhangtingxiqwq/article/details/134042245

通过倍增实现排序

类似基数排序，先排后面，再排前面

排的过程可以拿桶排优化

---

• 设 $h(i)=lcp(sa[rk[i]-1],i)$

• 有 $h(i)\ge h(i-1)-1$

CF1073G Yet Another LCP Problem （SA+ST表维护height+单调队列维护）

题目 https://www.luogu.com.cn/problem/CF1073G

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134043286

我们先求个SA，我们中途可能要求两个串的lcp，建个ST表维护。

然后把A和B混在一起按 $rk$ 排序。

我们先考虑用B查询A，反过来同理。我们用单调队列维护height，相同的要合并。

数论

质数、因数类题目

NOIP考虑数论最多在这一块

难分解质因数

数论类题目如果能分解质因数就很好做，但如果不能分解我们只能考虑一些巧妙的方法。

[AGC003D] Anticube （回归题目性质，回避数学问题）

题目：https://www.luogu.com.cn/problem/AT_agc003_d

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132153999

题目相当于求二分图最大匹配。然后可以分析出一堆性质，暴力分解 $10^3$ 引内的质数。然后剩下 $p^2$ 可以直接sqrt判断，$1e6$ 以内不存在 $pq$。然后再 $[1e6,1e10]$ 内如何区分 $p$ 和 $pq$ 呢？

对于从数学角度无法解决的问题，我们考虑回归题目性质。我们发现若 $p\ge 10^5$ 时，我们匹配 $p^2$ 至少要 $10^{1}0$，而这显然不存在。同理 $p^2{q}^2$ 更不可能存在，于是我们就回归题目性质，回避数学问题

ZR2639三色堇（维护题目所求[差值]）

题目：http://zhengruioi.com/problem/2639

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132325425

显然数会非常大，但题目求的是差值的平方，且第一个质数非常小，所以我们可以考虑维护差值。

exgcd / 解一元二次不定方程

https://blog.csdn.net/zhangtingxiqwq/article/details/132385405

exgcd

int exgcd(int a, int b, int &x, int &y) {
	int d=a; 
	if(b==0) x=1, y=0; 
	else {
		d=exgcd(b, a%b, y, x); 
		y-=a/b*x; 
	}
	return d; 
}

能背就背，背不了考场手推也有点小烦

解一元二次不定方程

1. 有解充要条件：令 $d=\gcd (a,b),c\mathrm{mod}d=0$
2. 我们可以exgcd求出 $ax+by=1$ 的解
3. 合法解：我们用 $x,y$ 分别乘上 $c$ 即可
4. 任意解：令 $p=b/d,q=a/d$，则 $x=x+kp,y=y-kq$

ABC315G Ai + Bj + Ck = X (1 <= i, j, k <= N)

题目：https://atcoder.jp/contests/abc315/tasks/abc315_g

给定 $x,y$ 的范围变成 $[1,n]$

我们在任意解中求上下界即可

整除分块

线性预处理整除分块

https://blog.csdn.net/zhangtingxiqwq/article/details/132596085

求：
$$\sum _{n=1}^m\sum _{i=1}^n\lfloor \frac{n}{i}\rfloor$$

直接用整除分块是 $O(n\sqrt{(}n))$。但我们考虑 $n-1\to n$ 只有哪些 $i$ 会发生变化，只有 $n$ 的因数。

所以我们线性筛出 $n$ 的因数个数，然后做个前缀和即可。

杜教筛

类欧几里得算法

众所周知，这东西不考

https://blog.csdn.net/zhangtingxiqwq/article/details/132718582

https://blog.csdn.net/zhangtingxiqwq/article/details/132792181

网络流

板子

网络最大流

https://blog.csdn.net/zhangtingxiqwq/article/details/132091032

1. bfs分层
2. dfs增广+当前弧优化

for(int &i=h[x]; i; i=d[i].n) {
	int y=d[i].y, z=d[i].z;  
	if(dep[y]!=dep[x]+1) continue; 
	if(z<=0) continue; 
	s=dfs(y, min(w, z)); ans+=s; w-=s; 
	d[i].z-=s; d[i^1].z+=s; 
	if(!w) break;  
}

上下界网络流

https://blog.csdn.net/zhangtingxiqwq/article/details/132093889

无源汇上下界可行流

https://blog.csdn.net/zhangtingxiqwq/article/details/132091530

新建源汇 $S,T$，若 $a\to b$ 有 $[c,d]$。网络流中上界肯定满足。

我们变成：

1. $S\to b,c$
2. $a\to T,c$
3. $a\to b,c-d$

因为我们求的是可行流。若 $a$ 能流 $c$ 到 $b$，则 $b$ 必然可以流 $c$ 回 $a$。前两天边就是为了实现这个判断的过程。最后一条是上界的限制。

有源汇上下界可行流

发现源点和汇点为特殊点，因为他们流入流量不等于流出流量。

所以 $T\to S,[0,+\infty ]$

然后跑无源汇上下界可行流

有源汇上下界最大流

在有源汇上下界可行流的残余网络中删掉附加变跑 $S\to T$ 最大流，最后加上可行流。

有源汇上下界最小流

同上，不过跑的是 $T\to S$ 的最大流。然后让可行流减去这个最小流。

网络流建模

网络最大流，我们求的是最大。

有些时候可能要考虑把最小转最大变成网络流模型

常见的套路有对点进行分类

二分图建模

二分图建模的核心是匹配

[NOI2019] 序列（至少转至多）

题目：https://www.luogu.com.cn/problem/P5470

总共 $K$ 个，至少 $L$ 个相同，说明至多 $K-L$ 个相同

直接建二分图，有一条万能边，可以随意匹配。剩下是 $c_i\to d_i$，表示恰好对应。万能边的流量就是我们想要的 $K-L$。

此题为费用流。

ABC320G G - Slot Strategy 2 (Hard)（二分套网络流）

题目 https://atcoder.jp/contests/abc320/tasks/abc320_g

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132927159

先枚举数字，然后要使最晚时间最早，考虑二分。

然后每个卷轴向前 $n$ 个合法时刻连边，然后跑一遍看看是否可行（两个卷轴不能同时停止）

显然最多 $n^2$ 条边。

CF1592F1 Alice and Recoloring 1 （行列点连边去掉点）

题目 https://www.luogu.com.cn/problem/CF1592F2

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133764633

我们继续分析性质，现在4操作可能做很多次，但任意两次之间必然是行列不相同的，而且其有意义当且仅当除 $(n,m)$ 外3个格子都有翻转的意义。

因此我们可以建一个朴素的网络流模型，点向行列连边。

但我们发现我们的点其实没有任何意义，我们直接把点变成边，行向列连，变成一个二分图即可。

[ARC142E] Pairing Wizards （根据限制转化为二分图+最小割）

题目 https://www.luogu.com.cn/problem/AT_arc142_e

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133623334

他的充要条件是是什么：

1. $a_i,a_j\ge min(b_i,b_j)$
2. 存在 $a_i\ge max(b_i,b_j)$

第一个条件直接预处理一下。第二个条件怎么处理？

我们发现如果第一个满足，第二个不满足，也就是 ：$\min (b_i,b_j)\le (a_i,a_j)\le \max (b_i,b_j)$，可以发现 $a_i\ge b_i$ 和 $a_j\ge b_j$ 两个必然一个成立，一个不成立！所以我们就可以对 $a,b$ 进行分类，每条都恰好连左右一个点。

然后最小割即可。

1024D. 排列 （最小割——选与不选）

题目 http://cplusoj.com/d/senior/p/SS231024D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134022318

选的意义代表把置换环整体位移

首先我们可以证明，每个位置至少选一个

然后我们就考虑仅 $A$ 选，仅 $B$ 选，$A,B$ 都选的代价，然后直接连边，求最小割即可。

1114D. 麻将机 （最小链覆盖转二分图）

题目 ：http://cplusoj.com/d/senior/p/SS231114D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134407471

每个点只要有一条出边做了，如果我们立刻做，是不会有代价的。

一个点如果本身没有，我们初始全做了，也是没有代价的。

因此我们转化成初始所有出现点都存在一条出边的问题。

假如有一条链，我们按倒序做，就会有1个代价。但如果结尾为原串未出现点，那么就没有代价。我们现在要基于这个东西做最小链覆盖。

首先我们要先把环去掉。显然一个强连通我们从一个进可以从任意一个出并遍历中间所有点，所以我们可以直接缩点变成DAG。

然后对于每个点，可以连向一个有出边的点，或者一个未出现的点，我们直接跑最大流。左边没流完的点就是代价。

多限制建模

即使是多限制类建模也很可能是基础二分图出发的

CF1408H Rainbow Triples （对点分类）

题目：https://www.luogu.com.cn/problem/CF1408H

对点进行分类。

• 0点分类：设有 $z$ 个0点，则答案上界为 $z/2$。所以我们就可以按左右分类
• 非0点分类：每个非0点如果左边点较少则为左部点，右边点较少则为右部点。因为点多的那边至少有 $z/2$ 个点。

可以发现我们分类后，非0点的类和0点的类恰好对应。我们在内部分别连边即可。最下面一层为题目的颜色限制。

图论转网络流

[ABC318G] Typical Path Problem （路径存在性问题）

题目 https://www.luogu.com.cn/problem/AT_abc318_g

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132644032

我们要找两条不交路径 $B\to A,B\to C$

先考虑不交性质，经典套路，拆点即可。

然后我们 $S\to B$ 流量为2。$A\to T,C\to T$ 流量为1即可。

模拟网络流

首先建出费用流，然后由于直接跑复杂度过大，可以用模拟割边、反悔贪心、模拟增广路的思想解决。

• 模拟割边类：根据最大流=最小割，我们可以考虑最小割怎么构造
  https://blog.csdn.net/zhangtingxiqwq/article/details/132093553
• 反悔贪心类：一个方法是使限制少的边先流完，再反悔去流限制大的
• 模拟增广路类：网络流本质就是找增广路。如果我们能模拟找增广路这个过程，就能实现模拟网络流。适用增广路不多的情况。

CF1408H Rainbow Triples （模拟割边类）

题目：https://www.luogu.com.cn/problem/CF1408H

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132093428

如果我们割边，要么割最上面的，要么割最小码的（某种颜色不选）。如果割上面的必然是割左边一段前缀和右边的一段后缀。

模拟割边法我们可以先假设一些边先被割了。此题中我们假设右边的边和颜色边全部被割。若一个颜色边对应的所有左边都被割了，那么颜色边和右边只需要割其中一种即可。

这个过程可以拿线段树维护。

[NOI2019] 序列（反悔贪心类+分类讨论）

题目：https://www.luogu.com.cn/problem/P5470

题解： https://blog.csdn.net/zhangtingxiqwq/article/details/132112120

此题中，如果能用限制流我们就不用自由流

我们先贪心把自由流全用了。对于限制流，有两种情况：

1. $\max a_i+b_i$，满足两个都没选
2. $\max a_k+b_i$ ，满足 $a_i$ 选了，$a_k$ 和 $b_i$ 没选。和这种情况的对偶情况

ZR23ABDay9紫罗兰（模拟增广路类 + bitset优化）

题目：http://zhengruioi.com/problem/2627

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132296366

可以发现增广路不超过 $O(n^2)$，我们可以逐条边加入，然后判断是否能从源点到此点。如果可以，就往汇点bfs。如果到达汇点，说明我们找到了一条新的增广路。

然而这样子不能保证网络流的正确性，因为我们没有维护反悔贪心这个过程。因此我们要建反悔边来维护这根增广过程。

对于一个点合法的出边集合（就是没有bfs过的点，我们可以拿bitset来做）

线性代数

线性基

1019B. 草莓路径(path) / P4151 [WC2011] 最大XOR和路径

题目 https://www.luogu.com.cn/problem/P4151

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133932506

链的放到线性基里

然后线性基通过高斯消元求主元（贪心思想，主元可以令那一位一定为1。那么就钦定主元为必选，这样一定更优）

高消的过程中也需要对链进行消元

最后用链来查询，丢01trie上维护

行列式

1. 交换两行，行列式变号
2. 一行整体加上 $k$ 倍另一行，行列式符号不变
3. 行列式如果只有其中对角线非0，那么它的值就是对角线上值的乘积

矩阵树定理

题目：https://www.luogu.com.cn/problem/P6178

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132152078

解决图的生成树计数问题，复杂度为 $O(n^3)$

构造一个度数矩阵，$f[x][x]$ 表示 $x$ 的度数（外向树为出度，内向树为入度），$g[x][y]$ 表示 $x\to y$ 这条边的边权。然后令 $h=f-g$，求 $h$ 的行列式即可。

CF446E DZY Loves Bridges （分治+线性代数）

题目 https://www.luogu.com.cn/problem/CF446E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133336367

哈希

树哈希

https://blog.csdn.net/zhangtingxiqwq/article/details/133146153

CF763D Timofey and a flat tree

题目 https://www.luogu.com.cn/problem/CF763D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133148959

判断同构，我们采用的是树哈希。

然后我们要换根，发现换根的时候只要 $x,y$ 的哈希值会改变，所以我们维护这两个点的哈希值即可。

分治

分治在很多题目中有妙用

分治

[广州 OI 2023 Day 1 C] 小明的幸运区间

题目 http://cplusoj.com/d/senior/p/GZOI2023D1C

法1：分治

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133218885

法2：启发式枚举

从大往小枚举 $max$，求出当前区间。当一边确定时，另一边满足单调性，可以直接二分。

那么我们直接枚举短的那边即可，另一边二分。

0926D. 隐形飞机(hide) （离线后分治处理）

题目 http://cplusoj.com/d/senior/p/SS230926D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133309861

考虑把所有区间和询问都丢到分治树上进行

法1：不跨中点分治

我们对于左区间维护区间内最右到哪，右区间维护最左（不跨中点）设为 $mxl,mnr$

对于一个询问，我们就是要查找是否存在一个跨中点的区间满足 $u\le l\le mxl,mnr\le r\le v$，这就是个经典二维数点问题，我们可以扫描线+树状数组维护。

复杂度 $O(n{\log }^{2}n)$

法2：跨中点分治

我们对于左区间算出每个点跨中点的最左在 $mnl$，右区间每个点跨中点的最右在 $mxr$。如果询满足条件，也就是 $l\le mxr,r\ge mnl$。

而 $mnl$ 和 $mxr$ 可以用单调队列维护，复杂度 $O(n\log n)$

中间相遇法

https://blog.csdn.net/zhangtingxiqwq/article/details/133321701

当分治的分界点不确定的时候，我们可以从左右同时开始找分界点

启发式分裂

https://blog.csdn.net/zhangtingxiqwq/article/details/133321898

与启发式合并类似。我们在分裂时删掉并新建小的，大的保留。

CF1181E2 A Story of One Country (Hard) （二维平面分治+中间相遇法+启发式分裂）

题目 https://www.luogu.com.cn/problem/CF1181E2

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133323437

考虑分治。我们每一次可以按其中一维进行分开。为了方便找到分界点，我们用中间相遇法。为了更好维护两个集合，我们采用启发式分裂。

cdq分治

https://blog.csdn.net/zhangtingxiqwq/article/details/132135114

解决三维偏序问题。一维分治，一维分治区间排序。

还有一维就用ds，常见是用树状数组维护。

cdq得难点在于把题目转化为三维偏序条件

GYM 104531 I. Bracket

题目：https://codeforces.com/gym/104531/problem/I

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132549832

我们有了前面的结论，对于一个区间 $[i,j]$，处理出 $nx{t}_i$ 和 $pr{e}_j$，再加上 $i<j$ 的条件，就可以至直接用cdq分治了。

笛卡尔树

笛卡尔树就是按数的大小关系进行分治

建树

https://blog.csdn.net/zhangtingxiqwq/article/details/132906457

int build() {
	int S[N]; 
	for(int i=1; i<=n; ++i) {
		while(top && T[S[top]].val < T[i].val) 
			T[i].son[0]=S[top], --top; 
		if(top) T[S[top]].son[1]=i; 
		S[++top]=i; 
	}
	top=0; 
	return S[1]; 
}

ZR23ABDay7矩形

题目：http://zhengruioi.com/problem/2612

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132255084

对 $b$ 去负，也就是满足 $\min a\ge \max b$ 的方案数。

对 $a,b$ 离散化后分别建笛卡尔树，我们可以求以每个 $i$ 为 $\min /\max$ 的方案数。

我们设 $a$ 求出来的是 $f$，$b$ 求出来的是 $g$，我们就是要求 ${\sum }_{l<r}{f}_l{g}_r$。我们固然可以前缀和来做，但这不方便动态维护，所以我们拿分治来弄。

如何动态维护见线段树部分

根号分治

Gym - 104386G CLC Loves SQRT Technology (Hard Version) （按出现次数分治）

题目 https://vj.imken.moe/contest/579844#problem/I

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132866002

相当于问 $[a_i=a_j]{\sum }_k\left(\genfrac{}{}{0ex}{}{i-1}{k}\right)\left(\genfrac{}{}{0ex}{}{n-j}{k}\right)2^{j-i-1}$

首先 $k$ 那一维范德蒙德卷积搞掉，剩下的我们考虑按出现次数分治。

若出现次数 $\le B$，直接暴力枚举，复杂度 $O(\frac{n}{B}{B}^2=nB)$

出现次数大于 $B$，则个数不超过 $\frac{n}{B}$，用fft计算即可

$B=2000$ 最合适

二分

1. 最大值最小、最小值最大…
2. 分数规划

最值最

P9755 [CSP-S 2023] 种树

题目 https://www.luogu.com.cn/problem/P9755

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133991517

最晚时间的最早

二分答案

再二分出每个点最晚什么时候被选

然后按照最晚被选的时间从前往后贪心

暴力跳即可

ZR23ABDay9紫罗兰（二分+网络流）

题目：http://zhengruioi.com/problem/2627

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132296366

考虑对原图建图网路流，但每条边有代价。我们要求出最某流量下的最小代价。

发现这个代价是所有有流量的边的max，也就是说我们求max的min。我们二分，然后只保留对应边跑网络流即可。

此题如果要进一步优化，可以逐条边加入，然后跑增广路。

构造

奇偶构造法

对于没有思路的，和数有关的构造题，可以考虑2的情况，也就是用奇偶来构造

构造时需要考虑：

1. 如何用奇偶构造合法
2. 非法是否能用奇偶反证

P9575 「TAOI-2」喵了个喵 Ⅳ

题目：https://www.luogu.com.cn/problem/P9575

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132471708

若 $n$ 为偶数，则 $x=1$。

1. 非法是否能用奇偶反证
   如果 $x$ 为奇，所有数取完gcd后也为奇，同时 $n$ 为奇，必然不合法。
   如果所以gcd都为偶，同样也不合法，因此我们就贪心取最小 $2^k$

2. 如何用奇偶构造合法
   现在我们相当于有一堆1/2，结合 $n$ 为奇数的性质，分类讨论构造即可。

[ARC141D] Non-divisible Set （因数构造）

题目 https://www.luogu.com.cn/problem/AT_arc141_d

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133248890

发现值域和选的数量有2倍差距，我们考虑按奇数和其2的幂次分组。那么每组至多选1个数，且每组至少选一个数。也就是每组恰选一个数。

考虑一组对前后的影响。考虑对后面时，显然每个数越大越好，对前面是，选的数越小越好。因此我们可以求出每个数的上下界。如果每个数都有合法的范围，那么就合法。

匹配构造

[ABC317G] Rearranging（二分图匹配构造）

题目：https://www.luogu.com.cn/problem/AT_abc317_g

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132517757

我们要构造满足条件。总共跑 $m$ 次二分图匹配，其实就是求 $m$ 次完美匹配。我们直接用二分图匹配结果即可。

[ARC154C] Roller （循环构造——固一枚一）

题目 https://www.luogu.com.cn/problem/AT_arc154_c

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133606890

题目问两个环是否能互转，我们把 $B$ 的连续段抽象成一个子序列，就是询问 $A$ 是否存在一个开头能形成这个子序列。

同时需要特判 $A$ 是否能直接旋转的情况。（如果没有连续段且 $A$ 和 $B$ 循环同构但不相同就无解）

交换构造

常见方法：

1. 差分
2. 奇偶
3. 逆序对

[ARC102F] Revenge of BBuBBBlesort! （奇偶+逆序对）

题目 https://www.luogu.com.cn/problem/AT_arc102_d

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133825414

1. 奇偶角度：永远只在奇数为或偶数位（判定1）
2. 逆序对角度：逆序对总数每次-3，所以必须为3的倍数（判定2）
3. 奇偶+逆序对角度：每次奇数位或偶数位逆序对-1，所以必然为总逆序对数量的⅓（判定3）

这些条件看起来只是必要条件，但我们可以打表可得其也是充分的

其他构造

CCPC2020 长春站L（大于等于类限制条件化减为加）

题目 https://vjudge.net/contest/587311#problem/D

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133840957

只有后两个限制条件是好做的，我们枚举首项，然后相当于一个后缀整体建 $k$ 即可。

然而对于限制1我们容易减成负，我们可以化减为加，考虑首先定的时候最小是怎样的 ：

因此我们化为后缀加即可。

CF1592F1 Alice and Recoloring 1 （分析性质+单独考虑子问题）

题目 https://www.luogu.com.cn/problem/CF1592F1

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133757947

显然操作2,3都没用，可以大胆猜测操作4最多只会操作一次，考虑操作4做2次以上，只有这两种情况：

而这两种都可以用6步以内的操作1表示出来。

重新回来考虑。如果只有操作1，每个位置是否需要翻转。

看起来是和右下角所以格子有关，但其实只和其右下4个格子相关。因此我们对于另外这3个格子，是否对其有一次真的操作并不重要，我们已经得到其的信息，就是其最后通过一堆下面或者是自己的操作使其由现在的操作。因此我们就可以直接得出每个格子是否需要1操作。

此时我们回到4操作，明显可发现，我们每次4操作，只会改变4个格子的状态（其他格子都是改变偶数个），因此我们暴力枚举即可

CF566E Restoring Map （信息构造）

题目 https://www.luogu.com.cn/problem/CF566E

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133870468

若非叶之间有连边，则必然存在两个集合交集为 $x,y$，然后可以区分叶子和非叶子，并且知道所有非叶连边

对于一个叶子，包含它的所有集合中最小的就是它的集合

假设有三个以上的非叶子节点（一个直接菊花，2个叶子节点集合只有2种，分为两个集合即可），我们对于每个非叶子节点只保留 $\le 1$ 的非叶点，那么两两不同。对于叶子节点我们把其集合里的所有叶子节点去掉，那样子就可以找到它的父亲了。

发现上述过程可以bitset优化。

1025C. 彩排 （排列构造——用置换环）

题目 http://cplusoj.com/d/senior/p/SS231025C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134035399

我们朴素构造是 $n^2$ 的，但数据范围希望我们 $\frac{n^2}{2}$，我们发现如果每次直接复制一遍浪费了很多可以合并的的，我们希望把可以合并的放在一起。

我们现在如果考虑置换环，我们要对置换环进行置换，也就是把对应的数“运”到对应的地方，可以发现期望步数是 $\frac{n}{2}$ 步的，而置换环的期望个数是 $\ln$ 的。

1102C. DESTRUCTION 3,2,1 （余数分类构造）

题目 http://cplusoj.com/d/senior/p/SS231102C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134191475

对于构造类题目，我们可以通过余数进行分类

博弈论

博弈论常见方法：

1. 奇偶考虑法
2. 假设法

CF838C Future Failure （奇偶考虑+假设法）

题目 https://www.luogu.com.cn/problem/CF838C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133362167

一个串定的时候，如果不删，其方案数是定的。如果是偶数则先手必胜。这个方案数是 $\frac{n!}{\prod a_i!}$。如果其为奇数，考虑 $n$ 的二进制，每个1恰好分给其中一个 $a$。（注意到 $\sum a=n$）

考虑拿走一个数，相当于乘上 $\frac{a}{n}$。如果奇数向继续保持奇数，则 $\frac{a}{n}$ 必须为奇数，而这样的 $a$ 恰好有一个。

我们回到博弈，考虑假设。假设存在一个子问题进入可以win，那么先手直接进。如果不存在，且当前有偶数种排法，先手在这层耗着就行。如果有奇数种排法，先手只能往下一层走。显然不能走到偶数种的串，但我们证明了一定可以走到奇数种的串，所以相当于串长-1，因此只与 $n$ 的奇偶性有关了。

所以我们现在只需要计算 $n$ 为偶数且选法为奇数的方案数。直接dp然后枚举子集维护 $\frac{1}{\prod a_i!}$ 即可。可以钦定lowbit必选来优化。

P4101 [HEOI2014] 人人尽说江南好 （局面不变法）

题目 https://www.luogu.com.cn/problem/P4101

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133711268

考虑第一步，只能变成 2 1 1 1 1。下一步只能变成 3 1 1 1 1 或 2 2 1 1 1，但下一步又可以变回 4 1 1 1 1，也就是使局面状态始终保持不变。

因此胜手必然可以构造 m m m m k 1 1 1 1 的局面。那么只和这样子的轮数有关了。

二分图博弈

https://blog.csdn.net/zhangtingxiqwq/article/details/133840227

一张二分图，Alice和Bob每人走一步，不能重复走，谁不能走谁输

结论：若存在最大匹配不包含初始点，则Bob赢，否则Alice赢

以上图为例，红色为最大匹配。

首先对于Alice第一步只能走黑边。而Alice无论走到哪个点，都有一条红边。（不然就不是最大匹配了 ）

那么Bob就走红边，此时回到左边，Alice就只能走黑边了。

---

实现上，我们先把初始点去掉跑一遍流，加上后在残余网络上再跑一遍

2020CCPC长春站H（奇偶博弈+二分图博弈）

题目 https://vjudge.net/contest/587311#problem/I

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133840132

首先先从奇偶考虑想一下，发现每个人操作都会改变和的奇偶性，所以两人轮到自己操作的奇偶性始终不变，因此这就变成了一个二分图。

直接二分图博弈即可。

其他

二进制

二进制中最常考的是异或，但其他东西也有妙用

异或比较大小

异或比较大小的关键是抓住最高位

CF1863F Divide, XOR, and Conquer （有效 / 全局最高位）

题目 https://www.luogu.com.cn/problem/CF1863F

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132629186

暴力dp是 $O(n^3)$ 的，于是我们找一下性质。

由于有大小比较关心，我们考虑最高位，但我们发现最高位会约去，所以我们尝试的做法是抓住有效 / 全局最高位

我们考虑 $[l,r]$ 异或和最高位为 $i$，若 $[l,k]$ 的第 $i$ 位为1，那么显然 $[l,k]$ 是合法的。那么我们只需要标记 $l$ 开头第 $i$ 位为1的区间都是合法的。（因为我们是从大倒序枚举区间，所以不会有后效性）

异或前后 1 的个数的奇偶性

https://blog.csdn.net/zhangtingxiqwq/article/details/132915268

考虑异或操作，其前后1的个数奇偶性不会发生改变

因为每位要么没1，要么保留1个1，要么同时消掉2个1

这个结论可以方便我们构造fwt的转移系数

转化为二进制类

0912C. 绘画（二维网格转化为&关系）

题目 http://cplusoj.com/d/senior/p/SS230912C?tid=64ffe834f5f3679386f2da4b

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132840291

我们考虑局部情况：

当最高位都为1的时候为黑，否则递归下去。思考哪个位运算都为1的时候才有效，&操作。因此我们可以归纳出一个点为白色的条件为 $i\&j=0$

此题还有另一种转化方法：

这样子转化后的条件是 $i\subseteq j$

二进制转三进制

CF1033F Boolean Computer （扩大状态，不变枚举量）

题目 https://www.luogu.com.cn/problem/CF1033F

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134219227

我们发现直接用二进制来做很难做，但我们可以观察其给的表

我们发现如果表示成和的形式是容易进行一一对应的

对于询问的时候，我们直接枚举每位有的和是多少，虽然状态是三次的，但是对于每个填法最多对应两个

所以我们通过扩大状态，不变枚举量来进行

或相关

对于或的题目，一般2个数使极限

[AGC015D] A or…or B Problem （贪心+分类讨论）

题目 https://www.luogu.com.cn/problem/AT_agc015_d

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133643686

我们首先把 $r$ 最高位1找出来。然后把 $l$ 翻折到上面的那一段都是可以算的。

把 $l$ 的最高位去掉，剩下的可以随意构造。所以从中间开始一直到那个位置对应的 $mx$ 也可以全部统计进去。

FWT

NOIP不考

FWT笔记存档 https://blog.csdn.net/zhangtingxiqwq/article/details/132922560

FWT小结 https://blog.csdn.net/zhangtingxiqwq/article/details/132922605

贪心

[ARC136C] Circular Addition

题目 https://www.luogu.com.cn/problem/AT_arc136_c

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133525236

考虑非环的情况，就是差分数组之和。

由于在非环情况我们在前面补0，所以我们这里要对全局 $mx$ 去max。

只是在环中的构造可能和链不太一样。对于初始枚举位置，不一定要让它就有自己一开始有的，因为这个东西可能是环末尾贡献过来的。

[ARC123C] 1, 2, 3 - Decomposition （分类讨论+打表）

题目 https://www.luogu.com.cn/problem/AT_arc123_c

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133772012

分类讨论+打表，不想细说

[ARC166D] Interval Counts （差分法）

题目 https://www.luogu.com.cn/problem/AT_arc166_d

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133694378

显然区间越少越好，而且区间一定是这样子放：

所以相邻之差为橙色区间-紫色区间数量。由于区间数越少越好，所以要么保留橙色区间，要买暴力紫色区间。

然后我们橙色和紫色区间贪心匹配即可。

单调性

NC257499 神奇编码（哈夫曼树+决策单调性）

题目 https://ac.nowcoder.com/acm/problem/257499

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/132912243

朴素思路是拿个优先队列维护，数的大小为第一维，树高为第二维。但复杂度炸了。

但我们发现一个性质，假如我们按顺序合并哈夫曼树，那么合并的结果必然满足单调不减，因此可以拿deque维护。

但如果和一开始混在一起就不好了，那么我们开两个队列即可。

限制类题目

限制类题目的常见做法：

1. 限制转不等式

限制转不等式

CF1394C Boboniu and String（二维变一维）

题目：https://www.luogu.com.cn/problem/CF1394C

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132212342

最大的最小，先二分。

考虑相似的本质为什么，具体内容参见数形结合部分。

求一堆区间是否有并，我们可以回去重新变成限制类问题。而这些限制就全部可以写成不等式的形式。因此我们可以推出 $x,y,x-y$ 的取值范围。最后根据范围构造是否有合法解即可。

其实也是可二维从三个维度变成一维的问题。

min、max式子的处理

0928B. 最长上升子序列 （拆min / max）

题目 http://cplusoj.com/d/senior/p/SS230928B

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133521713

枚举2，扫描线加入0。设 $j$ 个0，2的位置分别在 $x,y$，我们要求 $j+\min (s_x-f_j,s_y-g_j)$（$f,g$ 分别表示前 $j$ 个0前1的个数，$s$ 为1的前缀和）

我们来拆一下min，可得 $j-g_j+\min (s_x-f_j+g_j,s_y)$，设 $p_j=j-g_j,t_j=f_j-g_j$，求 $p_j+\min (s_x-t_j,s_y)$。$p$ 显然不用管，我们按 $s_x-s_y$ 分类即可。

我们可以用两个个数据结构，扫描线时对于 $j$，在DS1中 $\le t_j$ 贡献为 $p_j$，在DS2里大于 $t_j$ 贡献为 $-t_j+p_j$。查询时我们在 $s_x-s_y$ 计算贡献为 $p_j+s_y$，DS中计算贡献为 $sx-t_j+p_j$，我们只需要维护最大值即可。

由于只用维护前后缀max，直接树状数组就行。

2022CCPC 绵阳站D（尽量平衡min / max）

题目 https://vjudge.net/contest/587311#problem/H

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133844333

我们首先可以推一推性质：

• $p_i\ge \frac{1}{X}$
• $p_i\le \frac{1}{1-Y}$

所以我们按 $p$ 排序，$su{m}_x$ 必然是后缀，$su{m}_y$ 必然是前缀。

因此在 $X$ 定的时候，$Y$ 的范围显然也是确定的，我们直接二分然后前后10个左右扫一扫即可。

1101B. 线段树？？ （边界缩小最值维护）

题目 http://cplusoj.com/d/senior/p/CPNOIPB

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/134167852

边界扩大最值很好维护，但边界最小就很难维护，我们有两种方法：

1. 对于缩小的情况倒序进行，就变成扩大了
2. 维护 $mid$，暴力修改，复杂度是均摊的

数形结合 + 计算几何

对于数形结合的题目，一般会在下面题目中用：

1. 离散类
2. 两个属性问题

采用数形结合我们就可以考虑用面积法或扫描线来解决问题。

UVA11722（离散类+面积法）

本题数不可能整，非常离散数学。所以我们可以通过数形结合，也就是面积法来解决

CF1394C Boboniu and String （两个属性类）

题目：https://www.luogu.com.cn/problem/CF1394C

题解：https://blog.csdn.net/zhangtingxiqwq/article/details/132212342

其他看限制部分。

发现只有 B 和 N，而且相似的定义和顺序无关，所以我们可以转成二维平面中的点。发现每个操作相当于对于这个点往其中一个方向走。

而我们在二分后，每个点可以到达的地方就是平面上一个区域：

所以我们现在就是求一堆区间的并是否为空。

CF788D Finding lines （坐标系+y=x轴）

发现有横线和竖线，很难区分，所以我们考虑 $y=x$ 这条线，它可以和两种线区分出来，然后我们就可以把交点取出来。有了交点就很好判断横竖线了。

找交点的过程本质是二分，但交点有很多，我们采用分治会更好。

曼哈顿距离与切比雪夫距离的相互转化

假设已知原坐标中两点为 $(x_1,y_1),(x_2,y_2)$

求曼哈顿距离 $\to$ 转化为切比雪夫距离

令 $(x,y)=(x+y,x-y)$

求切比雪夫距离 $\to$ 转化为曼哈顿距离

令 $(x,y)=(\frac{x+y}{2},\frac{x-y}{2})$

相当于原图只能斜着走且每次只能走 $\frac{1}{2}$ 步。

判断两线段是否相交

https://blog.csdn.net/zhangtingxiqwq/article/details/133943208

我们做两次

每次把一条线段视为直线，判断另一条线段的两个点是否在直线的两侧

如果两次都符合，说明直线相交

判断是否在两侧我们可以求叉积然后判断乘积是否为负

struct Point {
	double x, y; 
	Point operator - (const Point &A) const {
		Point B; B.x=x-A.x; B.y=y-A.y; 
		return B; 
	}
	double operator ^ (const Point &A) const {
		return x * A.y - y * A.x; 
	}
};
namespace Cross {
	bool Line_cross(Point p1, Point p2, Point p3, Point p4) {
		double a1 = (p1 - p2) ^ (p3 - p2); 
		double a2 = (p1 - p2) ^ (p4 - p2); 
		if(a1 * a2 >= 0) return false; 
		return true; 
	}
	bool cross(Point p1, Point p2, Point p3, Point p4) {
		bool t1 = Line_cross(p1, p2, p3, p4); 
		bool t2 = Line_cross(p3, p4, p1, p2); 
		return t1 && t2; 
	}
}

分数规划

移项

0902T2 连接 connect（二分+移项）

题目 http://www.accoders.com/pdf/contest/4498.pdf

题解

对于求 $\frac{\sum p_i{l}_i}{\sum l_i}$ 在限定条件下的最大值，此类问题可以考虑二分答案并移项。

$$\begin{gathered} \frac{\sum p_i{l}_i}{\sum l_i}\ge k \\ \sum p_i{l}_i\ge k\sum l_i \\ \sum (p_i-k)l_i\ge 0 \end{gathered}$$

让维护和大于0的子段即可

高维前缀和

0922T2快哭了 (kk)（二进制高维前缀和）

题目 http://cplusoj.com/d/senior/p/SS230922B

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133183403

等价于求 $\left(\genfrac{}{}{0ex}{}{k}{i}\right)\times \left(\genfrac{}{}{0ex}{}{k}{j}\right)$ 为奇数的异或和，也就是满足 $(i|j)\&k=(i|j)$ 的 $(i,j)$ 的异或和，直接高维前缀和即可。

差分

[广州 OI 2023 Day 2 C] 简单的数据结构 （交错序列）

题目 http://cplusoj.com/d/senior/p/GZOI2023D2C

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133247058

考虑 $a_i-a_j$，就是 $[j+1,i]$ 的差分数组之和。由于选的段数无限制，全选正数。

全序关系

https://blog.csdn.net/zhangtingxiqwq/article/details/133698338

一个序列满足全序关系必须满足以下条件：

1. 反对称性：若 $a\le b$，则 $b\ge a$
2. 传递性：若 $a\le b$ 且 $b\le c$，则 $a\le c$
3. 完全性：$a\le b$ 或 $b\le a$

求导

https://blog.csdn.net/zhangtingxiqwq/article/details/133560750

打表

打表作用：

1. 猜结论验证
2. 状态规模

[ARC144C] K Derangement

题目 https://www.luogu.com.cn/problem/AT_arc144_c

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133607035

一开始猜的结论是前后 $k$ 个预处理，中间贪心。

打表可得规律：

可以发现是前面 $2k$ 连续块直接暴配，最后一段再用我想的贪心。

1014C. 制糊串 （输出完整表+特判特殊情况）

题目 http://47.92.197.167:5283/contest/412/problem/3

题解 https://blog.csdn.net/zhangtingxiqwq/article/details/133824842

场上猜结论，把上下界处理出来后，判断是否在范围内。

但打完暴力应该顺手把表输出。

发现AAAAAA，BBBBBB 的情况，$L+1$ 取不到

ABABABAB 的情况 $R-1$ 取不到