一道非常易错的定积分问题的本质详解

计算${\int }_0^{\frac{3\pi }{4}}\frac{dx}{2+\cos 2x}$

经典错误一

$$\begin{array}{rl}{\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{2+\cos 2x}& ={\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{2+2{\cos }^{2}x-1}={\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{{\sin }^{2}x+3{\cos }^{2}x}\\ & ={\int }_0^{\frac{3\pi }{4}}\frac{{\sec }^{2}x\mathrm{d}x}{3+{\tan }^{2}x}=\frac{1}{\sqrt{3}}{\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}\left(\frac{1}{\sqrt{3}}\tan x\right)}{1+{\left(\frac{1}{\sqrt{3}}\tan x\right)}^2}\\ & ={\left[\frac{1}{\sqrt{3}}\arctan \left(\frac{1}{\sqrt{3}}\tan x\right)\right]}_0^{\frac{3\pi }{4}}=-\frac{\pi }{6\sqrt{3}}\end{array}$$

错误分析一

这个问题的本质是函数$F(x)=\frac{1}{\sqrt{3}}\arctan \left(\frac{\tan x}{\sqrt{3}}\right)$在区间$[0,\pi ]$上有间断点$x=\frac{\pi }{2}$，因此不能用牛顿——莱布尼茨公式.

经典错误二

$$\begin{array}{rl}{\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{2+\cos 2x}& ={\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{2+2{\cos }^{2}x-1}={\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{{\sin }^{2}x+3{\cos }^{2}x}\\ & ={\int }_0^{\frac{3x}{4}}\frac{{\sec }^{2}x\mathrm{d}x}{3+{\tan }^{2}x}=\frac{1}{\sqrt{3}}{\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}\left(\frac{1}{\sqrt{3}}\tan x\right)}{1+{\left(\frac{1}{\sqrt{3}}\tan x\right)}^2}\\ & =\frac{1}{\sqrt{3}}{\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}\left(\frac{1}{\sqrt{3}}t\right)}{1+{\left(\frac{1}{\sqrt{3}}t\right)}^2}={\left[\frac{1}{\sqrt{3}}\arctan \frac{t}{\sqrt{3}}\right]}_0^{-1}\\ & =-\frac{\pi }{6\sqrt{3}}\end{array}$$

错误分析二

有的小伙伴就说了，我做换元$\tan x=t$之后，总没有间断点的问题了吧？总可以用牛莱公式了吧？但是这个换元本身就是有问题的，我们看不定积分的换元和定积分的换元有什么区别。
不定积分的第一类换元法如下：

不定积分的第二类换元法如下：

定积分的换元法如下：

对应的注：

我们可以看出，不定积分有两个换元法，但是定积分只有一个，定积分的换元法类似于不定积分的第二类换元法。也就是做$x=\phi (t)$换元，并且函数$x=\phi (t)$的值域覆盖住定积分的上下限.而经典错误二中的换元是把$\tan x$换成了$t$类似于不定积分的第一类换元，这个在定积分换元中是“不存在”的，想转换成定积分的换元，相当于做$x=\arctan t$的换元，但是这样的话，就要求$\arctan t$的值域可以覆盖掉积分的上下限，而$\arctan t$的值域是$\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$,覆盖不到定积分的上限$\frac{3\pi }{4}$,因此不满足定积分换元的前提条件.

正确解法一

求出“真正”的原函数

经典错误解法1的原函数如图：

真正的原函数的图像如图：

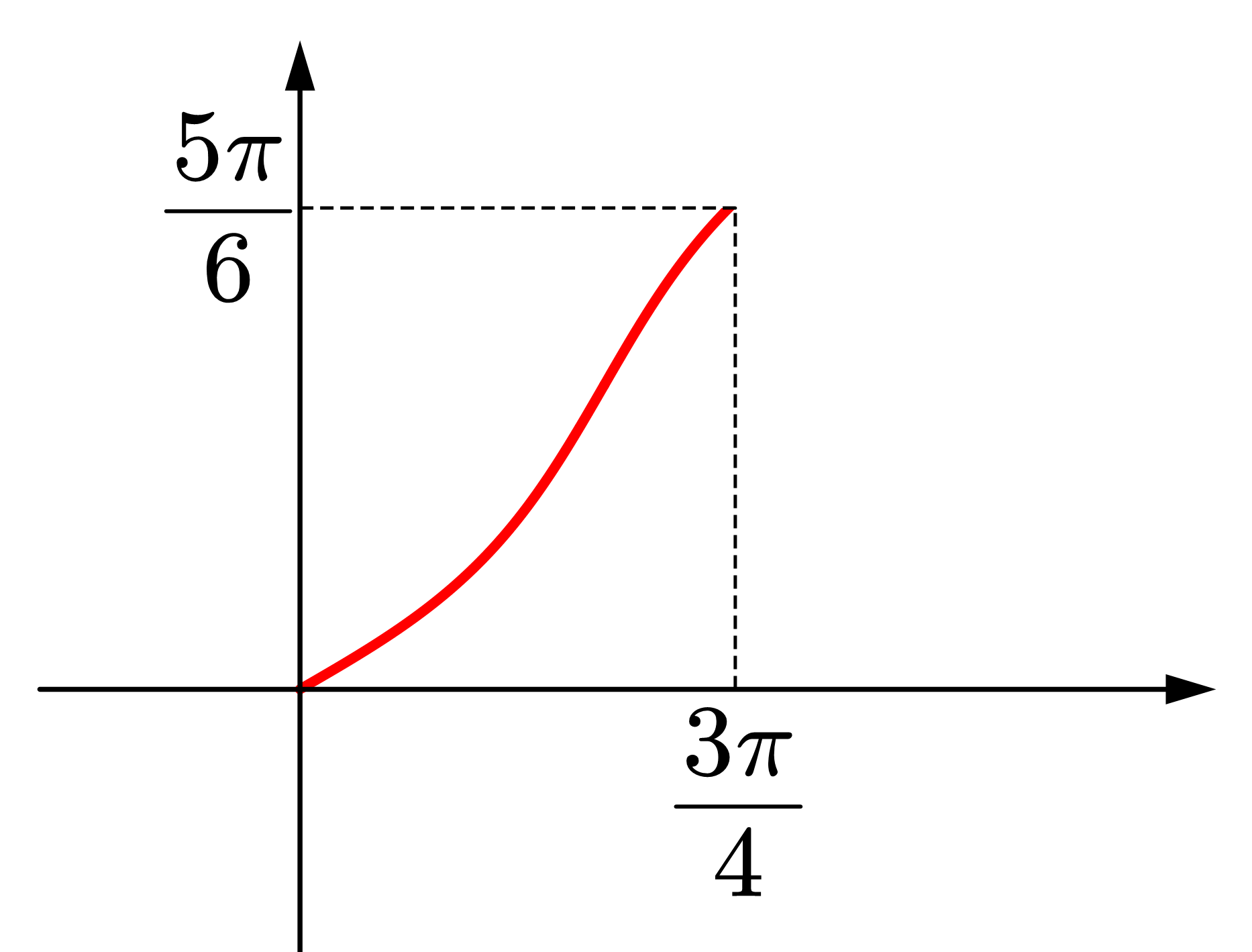
因此
$${\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{2+\cos 2x}=\frac{1}{\sqrt{3}}\arctan \left(\frac{\tan \frac{3\pi }{4}}{\sqrt{3}}\right)+\frac{\pi }{\sqrt{3}}=\frac{5\pi }{6\sqrt{3}}$$

正确解法二

将积分拆成两段：
$$\begin{array}{rl}{\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{2+\cos 2x}& ={\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{2+2{\cos }^{2}x-1}={\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{{\sin }^{2}x+3{\cos }^{2}x}\\ & ={\int }_0^{\frac{3\pi }{4}}\frac{{\sec }^{2}x\mathrm{d}x}{3+{\tan }^{2}x}=\frac{1}{\sqrt{3}}{\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}\left(\frac{1}{\sqrt{3}}\tan x\right)}{1+{\left(\frac{1}{\sqrt{3}}\tan x\right)}^2}\\ & =\frac{1}{\sqrt{3}}{\left[\arctan \left(\frac{\tan x}{\sqrt{3}}\right)\right]}_0^{\frac{\pi }{2}}+\frac{1}{\sqrt{3}}{\left[\arctan \left(\frac{\tan x}{\sqrt{3}}\right)\right]}_{\frac{\pi }{2}}^{\frac{3\pi }{4}}\\ & =\frac{\pi }{2\sqrt{3}}+\frac{-\pi }{6\sqrt{3}}+\frac{\pi }{2\sqrt{3}}=\frac{5\pi }{6\sqrt{3}}\end{array}$$

正确解法三

通过换元，改变定积分的区间
$$\begin{array}{rl}{\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{2+\cos 2x}& ={\int }_0^{\frac{3\pi }{4}}\frac{\mathrm{d}x}{{\sin }^{2}x+3{\cos }^{2}x},\left(x=\frac{\pi }{2}-t\right)\\ & ={\int }_{-\frac{\pi }{4}}^{\frac{\pi }{2}}\frac{\mathrm{d}t}{{\cos }^{2}t+3{\sin }^{2}t}\\ & ={\left[\frac{1}{\sqrt{3}}\arctan (\sqrt{3}\tan x)\right]}_{-\frac{\pi }{4}}^{\frac{\pi }{2}}\\ & =\frac{5\pi }{6\sqrt{3}}\end{array}$$