[强化学习]一文带你理清从Q-Learning到DDPG(Deep Deterministic Policy Gradient)算法思想

苏轼'

已于 2023-10-10 21:38:35 修改

阅读量2.3k

点赞数 4

文章标签：算法强化学习 pytorch

于 2021-11-05 11:21:22 首次发布

本文链接：https://blog.csdn.net/zhangxiaolil/article/details/121136331

版权

[强化学习]一文带你理清从Q-Learning到DDPG(Deep Deterministic Policy Gradient)算法思想

强化学习的五大要素：
State、Action、Reward、Discount factor （r）、P 转移概率。

Q-Learning思想过程

Q-learning是强化学习中基于价值的算法，是一种off-policy、免模型策略。
Q-Learning就是在环境的某一个时刻的状态(state)下，采取动作集中的一个动作a能够获得收益的期望，环境会根据agent的动作反馈相应的reward奖赏，Q-learning根据reward更新Q表格。
核心就是将state和action构建成一张Q_table表来存储Q值，然后根据Q值来选取能够获得最大收益的动作。

上伪代码：
在这里插入图片描述

初始时Q表格为空。
在每一个episode中智能体从环境s中基于e-greedy贪心的思想选择一个动作a。
注：
e-greedy:当超参数e设计为0.9时表示：有90%的概率选择Q表格中分数再大的action。否则有10%的概率随机选择动作。
将采取的动作a施加到环境中，并返回观测的状态s’,该动作的奖励。
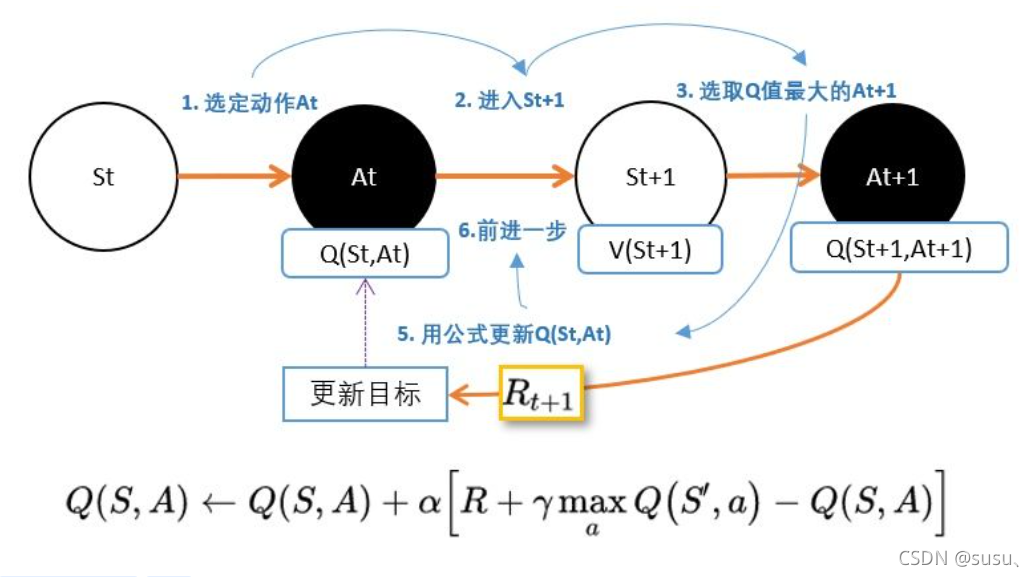
根据返回的信息更新Q表格：
(这个公式重点！)

更新当前Q(S,a):根据下一个状态s’中选取最大的Q ( s ′ , a ′ ) 值乘以衰变γ（即下一时刻最大动作的奖励折扣）加上真实回报值最为Q现实，而根据过往Q表里面的Q(s,a)作为Q估计。

5.更下当前状态。

DL与RL结合存在以下问题：

DL是监督学习需要学习训练集，强化学习不需要训练集只通过环境进行返回奖励值reward，同时也存在着噪声和延迟的问题，所以存在很多状态state的reward值都是0也就是样本稀疏
DL每个样本之间互相独立，而RL当前状态的状态值是依赖后面的状态返回值的。当我们使用非线性网络来表示值函数的时候可能出现不稳定的问题

DQN中的两大利器解决了以上问题

通过Q-Learning使用reward来构造标签
通过experience replay（经验池）的方法来解决相关性及非静态分布问题
使用一个MainNet产生当前Q值，使用另外一个Target产生TargetQ。

Q-Learning的局限：
其中最大的缺点就是Q-learning需要一个Q table，在状态很多的情况下，Q table会很大，查找和存储都需要消耗大量的时间和空间。

为此，使用神经网络代替查找Q表中Q值得计算以及查找过程。
可以用NN来近似 Q（S,A），以状态S和动作A为输入，输出对应的Q值。或者，另一种方式是，以状态作为输入，输入各种动作下对应的Q值。
引入神经网络的优点是可以方便地从所有输出中找到最高的Q值，从而决定最优的动作。
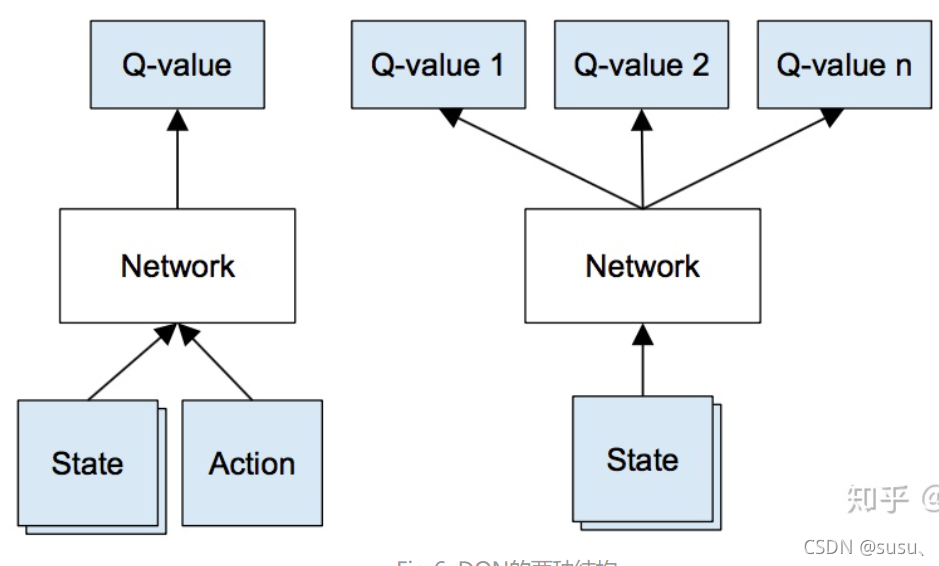
在这里插入图片描述
通常采用后者。

DQN

在这里插入图片描述

从代码中可以看到它有一个store experience的过程。即DQN采用了一个记忆库，用来存放之前的状态。
经验回放
初始时DQN与Qlearning一样会从环境中选取动作并执行行动得到环境返回的回报等。然后存储到记忆库中。只有当记忆库存储到一定容量之后才执行DQNPolicy更新策略。

经验池DQN中的记忆库用来学习之前的经历，又因为q-learning 是一种 off-policy 离线学习法, 它能学习当前经历着的,也能学习过去经历过的, 甚至是学习别人的经历，所以在学习过程中随机的加入之前的经验会让神经网络更有效率。
所以经验池解决了相关性及非静态分布问题。他通过在每个timestep下agent与环境交互得到的转移样本 (s ,a, r,s_) 储存到回放记忆网络，要训练时就随机拿出一些（minibatch）来训练因此打乱其中的相关性。

Q-target 目标网络

Q-targets的作用其实也是一种打乱相关性的机制，使用Q-targets会使得DQN中出现两个结构完全相同但是参数却不同的网络。
预测Q估计的的网络使用的是最新的参数。
预测Q现实的Target网络参数使用的却是很久之前的。

Q ( s , a ; ) 表示当前val网络的输出，用来评估当前状态动作对的值函数；
Q ( s , a ; ) 表示Target网络的输出。
可以解出targetQ并根据LossFunction更新估计网络的参数，每经过一定次数的迭代，将估计网络的参数复制给Target网络。
引入Target网络后，再一段时间里目标Q值使保持不变的，一定程度降低了当前Q值和目标Q值的相关性，提高了算法稳定性。

DQN训练过程：
在这里插入图片描述
补充阅读：深度强化学习之深度Q网络DQN详解

Sarsa

与DQN不同的是Sarsa是on-policy的更新方式。
它的行动策略和评估策略与DQN一样都是ε-greedy策略，也是采用Q-table的方式存储动作值函数。

sarsa伪代码：
在这里插入图片描述
从代码中可以看到Sarsa是先做出动作后更新。

Qlearning是先假设下一步选取最大奖赏的动作，更新值函数。然后再通过ε-greedy策略选择动作。
Sarsa算法，先通过ε-greedy策略执行动作，然后根据所执行的动作，更新值函数。

sarsa与Qlearning的不同之处：

在Q值的更新上，Q-learning中对下一个状态和动作采取的是max的操作，即每一步都选取Q值最大的动作。
而Sarsa则相对保守，在更新Q(s,a) 时基于的是下一个 Q(s′,a′)。

两个算法都用了epsilon-greedy来选择action。但是，Sarsa 是在learn之前是用epsilon-greedy选中一个action，并确定用这个action进行learn，所以下一步update的action就是要learn的action。所以当前learn的不一定是最大奖励的。而Q-learning对下一步的action取max，每步learn的都是眼前奖励最大的，但由于epsilon-greedy存在随机性，可能会跳出贪心，转变为随机选择，所以下一步update的action大概率不是要learn的。

总： Q-learnin是off-policy算法，而sarsa是on-policy算法。两者在算法上的区别就在于Q值更新的不同。换句话说，Q-learning在下一步更新时，考虑的是下一时刻中的最大Q值，而Sarsa是即时更新，在更新的时候，只考虑下一时刻的Q值。

Sarsa(lambda)算法
Sarsa(lambda)算法是Sarsa 的改进版，二者的主要区别在于：

在每次take action获得reward后，Sarsa只对前一步Q(s,a)进行更新，Sarsa(lambda) 则会对获得reward之前的步进行更新。
Sarsa(lambda)算法的流程如下：
在这里插入图片描述
从上图可以看出，和Sarsa相比，Sarsa(lambda)算法中多了一个矩阵E (eligibility trace)，它是用来保存在路径中所经历的每一步，因此在每次更新时也会对之前经历的步进行更新。

参数lambda取值范围为[0, 1] ，如果 lambda = 0，Sarsa(lambda) 将退化为Sarsa，即只更新获取到 reward 前经历的最后一步；如果 lambda = 1，Sarsa(lambda) 更新的是获取到 reward 前的所有步。lambda 可理解为脚步的衰变值，即离奶酪越近的步越重要，越远的步则对于获取奶酪不是太重要。

和Sarsa相比，Sarsa(lambda)算法有如下优势：

Sarsa虽然会边走边更新，但是在没有获得奶酪之前，当前步的Q值是没有任何变化的，直到获取奶酪后，才会对获取奶酪的前一步更新，而之前为了获取奶酪所走的所有步都被认为和获取奶酪没关系。Sarsa(lambda)则会对获取奶酪所走的步都进行更新，离奶酪越近的步越重要，越远的则越不重要（由参数lambda控制衰减幅度）。因此，Sarsa(lambda)
能够更加快速有效的学到最优的policy。

1.sarsa(0)是但不更新，每走一步更新一次，在获取到宝藏后，可能最开始会原地打转有一些重复无意义的步也被记录下来。
2.sarsa(n) 是回合更新，即只有当获取到宝藏之后才对最后一步进行更新，这样会导致他认为之前所走的每一步都是无意义的。
3.sarsa(lambda) 找到宝藏之后，对之前的所有步数进行更新，通过脚步衰减值控制离奖励不同远近的步数的Q值。

注意，该算法与Sarsa 算法不同的地方就是多乘了一个E(s, a) (Eligibility Trace”不可或缺性值”)，而这个E(s, a)又同时受γ和λ调控。并且在更新Q表的时候，不仅仅是更新一个Q(S,A)，而是整个Q表所有的Q值都被更新了。

策略梯度算法(Policy Gradient）

PG与DQN不同的是它是基于策略的RL算法。

DQN系列强化学习算法主要的问题主要有三点。

第一点是对连续动作的处理能力不足。DQN之类的方法一般都是只处理离散动作，无法处理连续动作。
第二点是对受限状态下的问题处理能力不足。
第三点是无法解决随机策略问题。Value Based强化学习方法对应的最优策略通常是确定性策略，而有些问题的最优策略却是随机策略。

Policy Based强化学习方法可解决以上value based的问题。

Policy gradient: 输出的这个 action 可以是一个连续的值, 之前的 value-based 方法输出的都是不连续的值, 然后再选择值最大的 action. 而 policy gradient 可以在一个连续分布上选取 action。
这样我们可以利用PG解决连续动作空间的问题。

PG算法思想：
在这里插入图片描述
可以看到PG是基于回合更新的，也就是说它只有当一个回合结束之后才能更新，而不能向DQN一样在回合中的每一个步进行更新。

补充阅读：
【强化学习】策略梯度（Policy Gradient）
策略梯度方法笔记

Actor Critic（演员评论家）

它合并了以值为基础 (比如 Q learning) 和以动作概率为基础 (比如 Policy Gradients) 两类强化学习算法。完美解决了PG不能基于batch更新的缺点。

Actor Critic有两套不同的体系, Actor 和 Critic, 他们都能用不同的神经网络来代替。

Actor网络其实就相当于PG，（基于策略的网络）输入S,输出当前S的action。
Critic相当于DQN可以进行单步更新。（基于价值的网络），输入Actor估计出来的action，输出该action的Q值。计算出td_error再根据这个td_error来更新Actor网络，使得下次Actor选出的action的reward最大化。

就像他的名字一样，右Actor演员来选取动作，由Critic评论家来点评Actor的动作，使得Actor进行改进。

Deep Deterministic Policy Gradient（DDPG）

在这里插入图片描述

DDPG算法是基于DPG算法所提出的，属于无模型中的actor-critic方法中的off-policy算法。
解决了Actor-Critic 神经网络每次参数更新前后都存在相关性，导致神经网络只能片面的看待问题这一缺点。
同时也解决了DQN不能用于连续性动作的缺点。
DDPG拆开来看，Deep是说明需要神经网络。 Deterministic的意思就是最终确定地只输出一个动作。 Policy
Gradient我们已经知道是策略梯度算法。
DDPG可以看成是DQN的扩展版，不同的是，以往的DQN在最终输出的是一个动作向量，对于DDPG是最终确定地只输出一个动作。而且，DDPG让
DQN 可以扩展到连续的动作空间。

网络结构：

DDPG的结构形式类似Actor-Critic。DDPG可以分为策略网络和价值网络两个大网络。
DDPG延续DQN了固定目标网络的思想，每个网络再细分为目标网络和现实网络。

策略网络：Actor
输入：s
输出：a

Actor还有一个相同结构但不同参数的目标网络，是用来更新价值网络Critic的。两个网络都是输出动作action。

价值网络：Critic
输出：出当前状态的价值 q-value。

Critic的eval网络输入：当前Actor的估计网络输出的动作action
Critic的target网络输入：当前状态的观测值和Actor的目标网络输出的动作action。

Actor的目标是找到一个动作a能使得输出的价值Q最大。优化策略网络的梯度就是要最大化价值网络输出的这个Q值。
Critic作用就是来拟合价值函数 Qω(s,a)。

思想过程：
在这里插入图片描述
现在我们回到DDPG，作为DDPG，Critic当前网络，Critic目标网络和DDQN的当前Q网络，目标Q网络的功能定位基本类似，但是我们有自己的Actor策略网络，因此不需要ϵ−贪婪法这样的选择方法，这部分DDQN的功能到了DDPG可以在Actor当前网络完成

说白了是一种Actor Critic的一种，差异不大。
在这里插入图片描述

代码：
经验池

class Memory(object):
    def __init__(self, capacity, dims):
        self.capacity = capacity
        self.data = np.zeros((capacity, dims))  # capacity行  dims列  记忆库的形状矩阵
        self.pointer = 0  # 指向当前那行值

    # 存贮
    def store_transition(self, s, a, r, s_):
        transition = np.hstack((s, a, r, s_))  # 按水平方向进行叠加 相当于多少列

        index = self.pointer % self.capacity  # replace the old memory with new memory
        self.data[index, :] = transition  # 矩阵切片   对第index行进行赋值
        self.pointer += 1

    # 采样  --行数
    def sample(self, n):
        assert self.pointer >= self.capacity, 'Memory has not been fulfilled'
        indices = np.random.choice(self.capacity, size=n)  # 从0~capacity个行中随机取出n。但是有重复（indices 是ndarray）
        return self.data[indices, :]  # 一起返回这么些行的内容 （返回类型：ndarray）

Actor网络：

def get_actor(input_state_shape, name=''):
     inputs = tl.layers.Input(input_state_shape, name='A_input')
     x = tl.layers.Dense(n_units=30, act=tf.nn.relu, W_init=W_init, b_init=b_init, name='A_l1')(inputs)
     x = tl.layers.Dense(n_units=a_dim, act=tf.nn.tanh, W_init=W_init, b_init=b_init, name='A_a')(x)
     x = tl.layers.Lambda(lambda x: np.array(a_bound) * x)(x) 
     return tl.models.Model(inputs=inputs, outputs=x, name='Actor' + name)

Critic网络：

def get_critic(input_state_shape, input_action_shape, name=''):
     s = tl.layers.Input(input_state_shape, name='C_s_input')
     a = tl.layers.Input(input_action_shape, name='C_a_input')
     x = tl.layers.Concat(1)([s, a])
     x = tl.layers.Dense(n_units=60, act=tf.nn.relu, W_init=W_init, b_init=b_init, name='C_l1')(x)
     x = tl.layers.Dense(n_units=1, W_init=W_init, b_init=b_init, name='C_out')(x)
     return tl.models.Model(inputs=[s, a], outputs=x, name='Critic' + name)

🥦🐥，搬运工的日常。

苏轼'

关注

4
点赞
踩
22

收藏

觉得还不错? 一键收藏
打赏
0
评论
[强化学习]一文带你理清从Q-Learning到DDPG(Deep Deterministic Policy Gradient)算法思想

[强化学习]一文带你理清从Q-Learning到DDPG(Deep Deterministic Policy Gradient)算法思想强化学习的五大要素：State、Action、Reward、Discount factor （r）、P 转移概率。Q-Learning思想过程Q-learning是强化学习中基于价值的算法，是一种off-policy、免模型策略。Q-Learning就是在环境的某一个时刻的状态(state)下，采取动作集中的一个动作a能够获得收益的期望，环境会根据agent的动
复制链接

扫一扫