稀疏矩阵的三元组表示的应用(2)

问题代码：

问题描述: 采用三元组存储稀疏矩阵，设计两个稀疏矩阵相加的运算算法  
输入描述：两个稀疏矩阵 
程序输出：相加运算后的结果。 

---

#include"tup.h"  
int main()  
{  
    TSMatrix ta,tb,tc;  
    int A[M][N]=  
    {  
        {0,0,1,0,0,0,0},  
        {0,2,0,0,0,0,0},  
        {3,0,0,0,0,0,0},  
        {0,0,0,5,0,0,0},  
        {0,0,0,0,6,0,0},  
        {0,0,0,0,0,7,4}  
    };  
    int B[M][N]=  
    {  
        {0,0,10,0,0,0,0},  
        {0,0,0,20,0,0,0},  
        {0,0,0,0,0,0,0},  
        {0,0,0,50,0,0,0},  
        {0,0,20,0,0,0,0},  
        {0,0,0,10,0,0,4}  
    };  
    CreatMat(ta,A);  
    CreatMat(tb,B);  
    printf("A:\n");  
    DispMat(ta);  
    printf("B:\n");  
    DispMat(tb);  
    if(MatAdd(ta, tb, tc))  
    {  
        printf("A+B:\n");  
        DispMat(tc);  
    }  
    else  
    {  
        printf("相加失败\n");  
    }  
    return 0;  
}  





bool MatAdd(TSMatrix a,TSMatrix b,TSMatrix &c)  
{  
    int i,j;  
    ElemType va,vb,vc;  
    if (a.rows!=b.rows || a.cols!=b.cols)  
        return false;                        //行数或列数不等时不能进行相加运算  
    c.rows=a.rows;  
    c.cols=a.cols;       //c的行列数与a的相同  
    c.nums=0;  
    for(i=0; i<M; i++)  
        for(j=0; j<N; j++)  
        {  
            Assign(a,va,i,j);  
            Assign(b,vb,i,j);  
            vc=va+vb;  
            if(vc)  
                Value(c,vc,i,j);  
        }  
    return true;  
}  

---

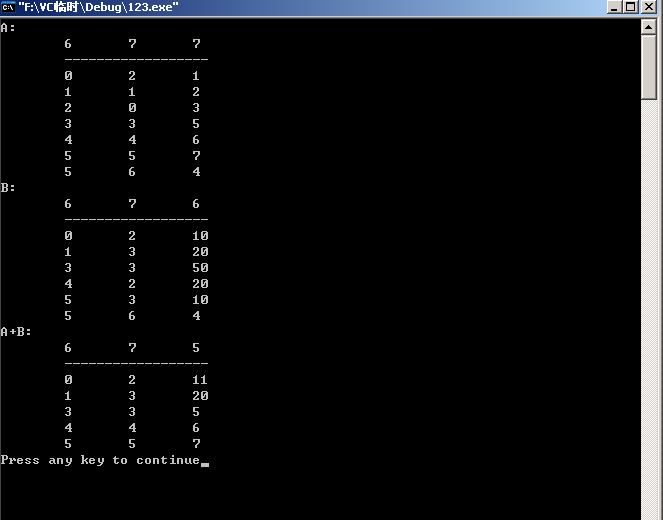
运行结果：

---

知识点总结：

稀疏矩阵的相加.

---