数据结构第一讲

第一个例子

老师以书架上存放书为例子来讨论。
在书架上如何防治书呢？要考虑书的规模。
第一种方案：
放书的方式，随便放
如何查找呢？所有的都要遍历。如果书的规模很大时，找一本书将会花很多时间。

第二种方案：
按照字母顺序存储书籍，我们找一本书时，可以按照字母顺序找书，但是放置书的时候，需要后移所有的书籍才能插入进去。也有缺点。

第三种方案：
结合实际。我们将书首先归类，将大规模的书籍划分到一个类中，然后再去按照二分查找方法找书。

如何进行分类呢？每类书籍要分配多大的空间呢？我们分类时，要分多细致呢？

启示

总结，解决问题的方法和数据的组织方式是相关的。

第二例子

写一个printN函数，该函数能够将N正整数以下的每个数据依次打印出来。有两种方案。
第一种方案：
main函数：

#include <stdlib.h>
#include <stdio.h>

#define LINE_MAX 16
static int printN1(int N);
static int printN2(int N);

int main(void)
{
  int ret = 0;
  int n = 100;
  printf("\n use printf 1 is :\n");
  printN1(n);
  printf("\n use printf 2 is :\n");
  printN2(n);
 printf("\n");
}

循环过程：

static int printN1(int n)
{
    int line = LINE_MAX;
    int i = 0;

    if(n <= 0)
    {
        return -1;
    }


    for(i = 0;i < n;i++)
    {
        if((n-i)%line == 0)
            printf("\n");
        printf("%d,",n-i);
    }
    return 0;
}

迭代过程：

static int printN1(int n)
{
    int line = LINE_MAX;
    int i = 0;

    if(n <= 0)
    {
        return -1;
    }


    for(i = 0;i < n;i++)
    {
        if((n-i)%line == 0)
            printf("\n");
        printf("%d,",n-i);
    }
    return 0;
}

10万次的程序执行结果为：

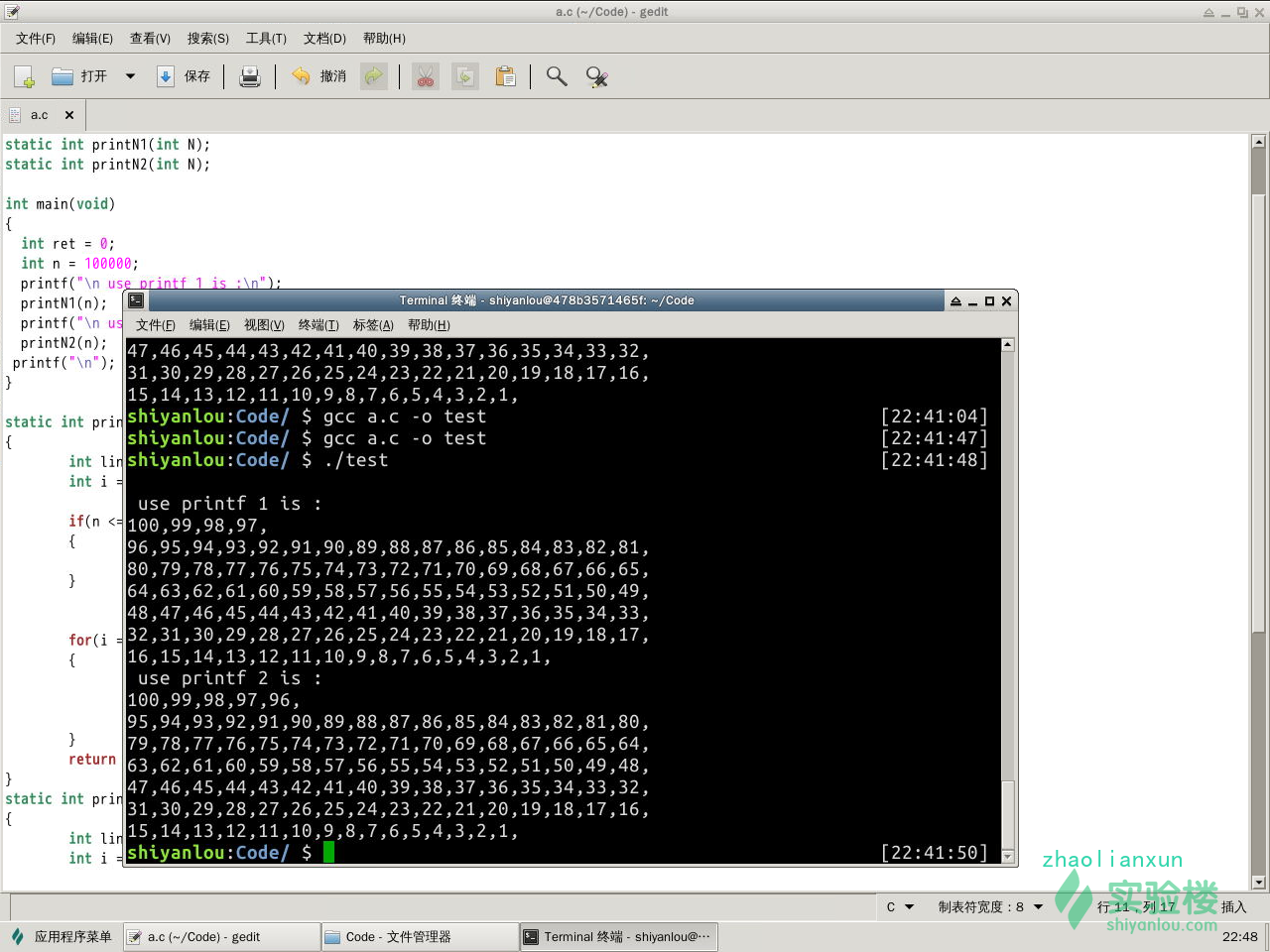
使用递归的算法的时候，当迭代次数为10万次的时候，仍然能够递归打印输出。改为100万次，只能输出825472次就结束了，出现segment段错误。表示进程的所有的空间已经被占据全部，仍然不够程序使用。

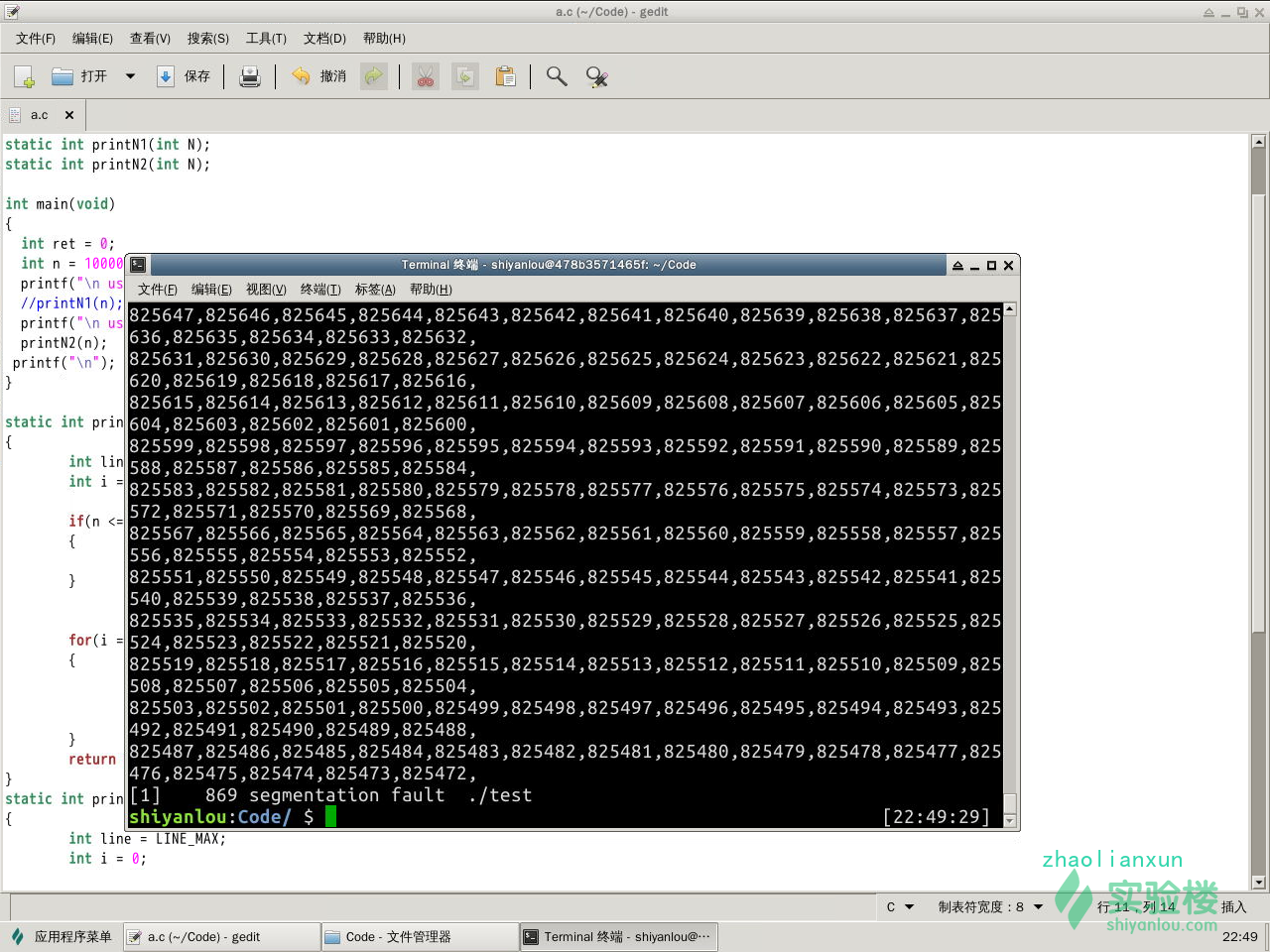
100万次后递归的执行结果

启示

这里，老师说程序的执行效率与程序占用的空间是有关系的。
但是这里程序已经无法执行了，何谈效率呢？当然递归也算是一种算法，是一种解决方式，影响了程序的执行结果。

第三个例子

多项式
$F(x) = a0+a1 *$${x^1 }$+….+an * ${x^n }$
main函数

int main(void)
{
    int ret = 0;
#if 0
    int n = 100;
    printf("\n use printf 1 is :\n");
    printN1(n);
    printf("\n use printf 2 is :\n");
    printN2(n);
    printf("\n");
#endif
    int n = 10;
    double a[11] = {12,14,33,33,42,43,89,33,67,56,45};
    int x = 4;
    int sum = 0;
    printf("\n use f1 is :\n");
    sum = f1(n,a,x);
    printf("sum is:%d;\n",sum);
    printf("\n use f2 is :\n");
    sum = f2(n,a,x);
    printf("sum is:%d;\n",sum);

}

直接转化：

static int f1(int n,double a[],int x)
{
    int i = 0;
    int p =  a[0];
    for (i = 1;i <= n;i++)
        p += a[i] * pow(x,i);

    return p;
}

提取公因式

static int f2(int n,double a[],int x)
{
    int i = 0;
    int p =  a[n];
    for (i = n;i >= 1;i--)
        p = a[i-1] + p*x;

    return p;
}

运行结果是：

shiyanlou:Code/ $ gcc  -o test a.c -lm                               [23:23:25]
shiyanlou:Code/ $ ./test                                             [23:26:20]

 use f1 is :
sum is:67219604;

 use f2 is :
sum is:67219604;
shiyanlou:Code/ $  

启示

解决问题的效率和运用算法的巧妙程度有关系。

练习

求如下多项式的和
给定另一个100阶多项式 ，用不同方法计算并且比较一下运行时间？
$F(x) = 1+1 *$${x^1 }$+….+$\dfrac{1 }{n}$ * ${x^n }$
main函数中增加时间计算：

#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#include <time.h>

static double f3(double x);
static double f4(double x);

int main(void)
{
    int ret = 0;
    int n = 100;
    double a[100] = {0};
    int x = 4;
    double sum = 0;
    int i = 0;
    time_t start,stop;
    double  duration;
    int time = 1000;

    x = 1.1;
    printf("\n use f3 is :\n");
    start = clock();
    for(i = 0;i < time;i++)
        sum = f3(x);
    stop = clock();
    printf("sum is:%f;\n",sum);
    duration =(double) (stop - start) / (CLOCKS_PER_SEC);
    printf("duration = %f\n",duration);

    x = 1.1;
    printf("\n use f3 is :\n");
    start = clock();
    for(i = 0;i < time;i++)
        sum = f4(x);
    stop = clock();
    printf("sum is:%f;\n",sum);
    duration =(double) (stop - start) / (CLOCKS_PER_SEC);
    printf("duration = %f\n",duration);

}

直接翻译的代码：

static double f3(double x)
{
    double  p = 0;
    int     i = 0;
    double  a[101];

    for(i = 1;i <= 100;i++)
        a[i] = (double)1/i;

    for(i = 1;i <= 100;i++)
        p += a[i]*pow(x,i);
    p++;

    return p;
}

经过提取公因子x后，函数实现为：

static double f4(double x)
{
    double  p = 0;
    int     i = 0;
    double  a[101];

    for(i = 1;i <= 100;i++)
        a[i] = (double)(1)/(double)(i);

    p = a[100]; 
    for(i = 99;i > 0 ;i--)
    {
        p = (a[i] + x*p);
    }

    p++;

    return p;
}

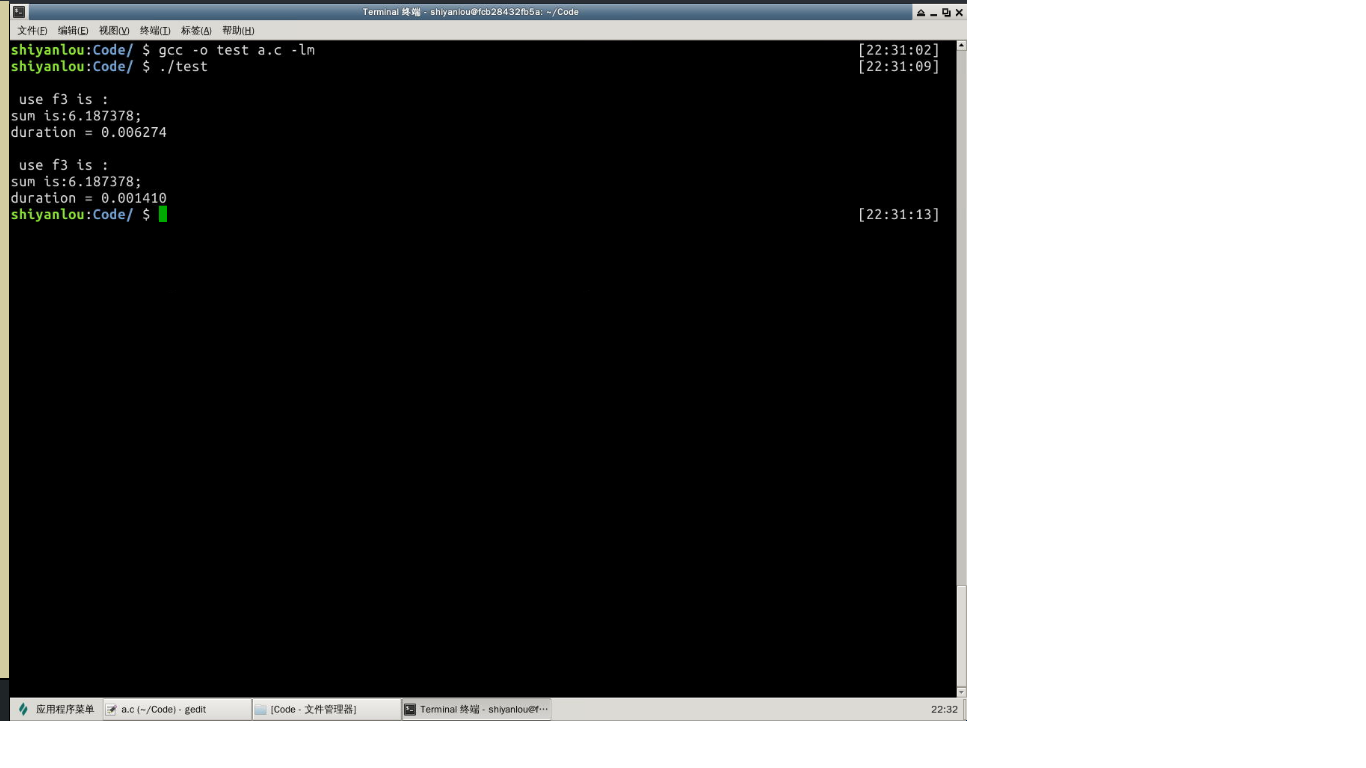
结果：

通过测试结果可以看到第一种方法的耗时是第二种方法耗时的5倍左右。