单调队列+单调栈（stl使用结合）

原创已于 2022-04-08 22:19:47 修改 · 932 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯 #c++ #gnu

于 2022-03-02 18:01:04 首次发布

这篇博客介绍了如何使用滑动窗口算法解决数组中的最大值和最小值问题。给出了两个实例，分别是求广告牌的最大面积和动态计算数组中滑动窗口的最大值和最小值。在广告牌问题中，通过维护一个单调栈找到每个位置的最大高度及其左右边界，从而计算最大面积。在滑动窗口问题中，利用双端队列动态维护窗口内的最大值和最小值。这两个问题都展示了滑动窗口在数组操作中的应用。

广告印刷（模板题）

Description

最近，afy决定给TOJ印刷广告，广告牌是刷在城市的建筑物上的，城市里有紧靠着的NN个建筑。afy决定在上面找一块尽可能大的矩形放置广告牌。我们假设每个建筑物都有一个高度，从左到右给出每个建筑物的高度H1,H2…HNH1,H2…HN，且0<Hi≤1,000,000,0000<Hi≤1,000,000,000，并且我们假设每个建筑物的宽度均为1。要求输出广告牌的最大面积。

Input

第一行是一个数nn (n≤400,000n≤400,000 ）

第二行是nn个数，分别表示每个建筑物高度H1,H2,≤,HNH1,H2,≤,HN，且0<Hi≤1,000,000,0000<Hi≤1,000,000,000。

Output

输出文件 ad.out 中一共有一行，表示广告牌的最大面积。

Samples

Input 复制

6
5 8 4 4 8 4

Output

#include<bits/stdc++.h>
using namespace std; 
#define N 1000005

int h[N],L[N],R[N];//创建两个数组进行操作 
stack<int>s;//创建一个栈，用来进行数据筛选，其中存储的是数组中元素的下标 


int main()
{
	int n,i;
	int maxx=0;
	cin>>n;
	for(i=1;i<=n;++i)
	{
		cin>>h[i];//将数据输入到数组中 
	}
	for(i=1;i<=n;i++)//寻找每个点的左边界 
	{
		//开始进行操作，每次存入到栈中的都是所遍历元素前面元素的下标 
		while(!s.empty()&&h[i]<=h[s.top()])//当栈不为空并且栈首元素比遍历的元素大的话 
		{
			s.pop();//删除栈首直到栈首元素比所遍历的元素小 
		}
		if(s.empty())//清空了所有的栈中元素，证明该点的左边界可以扩展到第一个 
		{
			L[i]=1;
		}
		else//由于是寻找左边界所以+1 
		{
			L[i]=s.top()+1;
		}
		s.push(i);//将元素压入栈中 
	}
	while(!s.empty())//将栈清空为寻找右边界创造条件 
	{
		s.pop();
	}
	for(i=n;i>=1;i--)//寻找每个点的右边界，同求左边界 
	{
		while(!s.empty()&&h[i]<=h[s.top()])
		{
			s.pop();
		}
		if(s.empty())
		{
			R[i]=n;
		}
		else
		{
			R[i]=s.top()-1;
		}
		s.push(i);
	}	
	for(i=1;i<=n;++i)
	{
		maxx=max(maxx,h[i]*(R[i]-L[i]+1));
	}
	cout<<maxx;
	return 0;
}

滑动窗口（模板题）

Description

给一个长度为NN的数组，一个长为KK的滑动窗体从最左端移至最右端，你只能看到窗口中的KK个数，每次窗体向右移动一位，如下图：

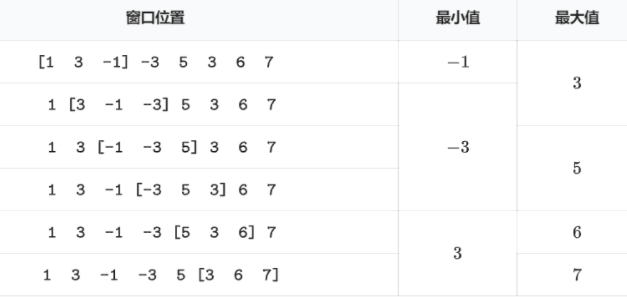
你的任务是找出窗体在各个位置时的最大值和最小值。

Input

第1行：两个整数NN和KK；
第2行：NN个整数，表示数组的NN个元素(≤2×109≤2×109)；

Output

第一行为滑动窗口从左向右移动到每个位置时的最小值，每个数之间用一个空格分开；
第二行为滑动窗口从左向右移动到每个位置时的最大值，每个数之间用一个空格分开。

Samples

Input 复制

8 3
1 3 -1 -3 5 3 6 7

Output

-1 -3 -3 -3 3 3
3 3 5 5 6 7

Hint

对于100%的数据，K≤N≤106K≤N≤106。

#include<bits/stdc++.h>
using namespace std;
const int x=1e6+5;
int a[x];

deque<int> q,dp;

int main()
{
	int n,i,k;
	cin>>n>>k;
	for(i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(i=1;i<=n;i++)
	{
		while(!q.empty()&&i-q.front()>k-1)
		{
			q.pop_front();
		}
		while(!q.empty()&&a[q.back()]>a[i])
		{
			q.pop_back();
		}
		q.push_back(i);
		if(i>=k)
		{
			cout<<a[q.front()]<<" ";
		}
	}
	cout<<endl;
	for(i=1;i<=n;i++)
	{
		while(!dp.empty()&&i-dp.front()>k-1)
		{
			dp.pop_front();
		}
		while(!dp.empty()&&a[dp.back()]<=a[i])
		{
			dp.pop_back();
		}
		dp.push_back(i);
		if(i>=k)
		{
			cout<<a[dp.front()]<<" ";
		}
	}
	
	
	
	return 0;
 }