算法分析与设计总结---分治算法

---

前言

算法分析与设计课程学习后的一些总结，本文主要介绍分治算法。

---

一、基本思想及策略

设计思想：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

分治策略：对于一个规模为 n 的问题，若该问题可以容易地解决（比如说规模 n 较小）则直接解决，否则将其分解为 k 个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题
的解合并得到原问题的解。这种算法设计策略叫做分治法。

如果原问题可分割成 k 个子问题，1<k≤n，且这些子问题都可解并可利用这些子问题的解求出原问题的解，那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

二、使用场景

分治法所能解决的问题一般具有以下几个特征：

1. 该问题的规模缩小到一定的程度就可以容易地解决
2. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
3. 利用该问题分解出的子问题的解可以合并为该问题的解；
4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。
   第一条特征是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加；
   第二条特征是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用；
   第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。
   第四条特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。

三、基本步骤

分治法在每一层递归上都有三个步骤：
step 1 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；
step 2 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题；
step 3 合并：将各个子问题的解合并为原问题的解。
它的一般的算法设计模式如下：
Divide-and-Conquer（P）

1. if |P|≤ n0
2. then return(ADHOC§)
3. 将P分解为较小的子问题 P1,P2,…,Pk
4. for i←1 to k
5. do yi ← Divide-and-Conquer(Pi ) △ 递归解决 Pi
6. T ← MERGE( y1,y2,…,yk ) △ 合并子问题
7. return(T)
   其中|P|表示问题P的规模； n0 为一阈值，表示当问题P的规模不超过 n0 时，问题已容易直接解出，不必再继续分解。ADHOC§是该分治法中的基本子算法，用于直接解小规模的问题P。因此，当P的规模不超过 n0 时直接用算法ADHOC§求解。算法MERGE( y1,y2,…,yk )是该分治法中的合并子算法，用于将P的子问题 P1,P2,…,Pk 的相应的解 y1,y2,…,yk 合并为 P 的解。

四、时间复杂度分析

一个分治法将规模为 n 的问题分成 K 个规模为 n/m 的子问题去解。设分解阀值 n0=1 ，且 adhoc 解规模为 1 的问题耗费 1 个单位时间。再设将原问题分解为 K 个子问题以及用 merge 将 K 个子问题的解合并为原问题的解需用 f(n) 个单位时间。用 T(n) 表示该分治法解规模为|P|=n的问题所需的计算时间，则有：

T(n)=KT(n/m)+f(n)

五、基于分治的算法

1.建堆

性质维护

背景：假设在数组A中，元素A[i]为完全二叉树的左、右两个孩子都已构成堆，但A[i]与两个孩子间不符合堆的性质，需要将其调整，使之满足堆的性质。

问题描述：数组A[1…n]预期存储一个完全二叉树，其中以A[i]为父节点的左、右子树已经构成最大堆，进行调节后，使A[i]为根节点的二叉树满足最大堆的性质。

问题思路：
第一步，将A[i]与左右节点进行比较，无非两种情况：与左叶子节点交换，或者与右叶子节点交换；
第二步，交换后，被交换的叶子节点可能不满足堆的性质，需要继续进行调节；
第三步[问题分解]，以被交换的叶子节点为根节点，继续判断调整，将原问题转化成小规模的问题（减少了二叉树的一层）；
第四步，使用递归处理

伪代码：

MAX-HEAPIFY(A,i)
	l =2i
	r =2i+1
	if l <= A.length and A[l] > A[i]
		then largest = l
	else largest = i
    if r <= A. length and A[r] > A[largest]
    	then largest = r
    if largest != i
    	then exchange A[i] <-> A[largest]
    		MAX-HEAPIFY(A,largest)

建堆

问题描述
• 输入：数组A[1…n]
• 输出：重排后的数组A[1…n]，元素间构成一个堆
伪代码描述
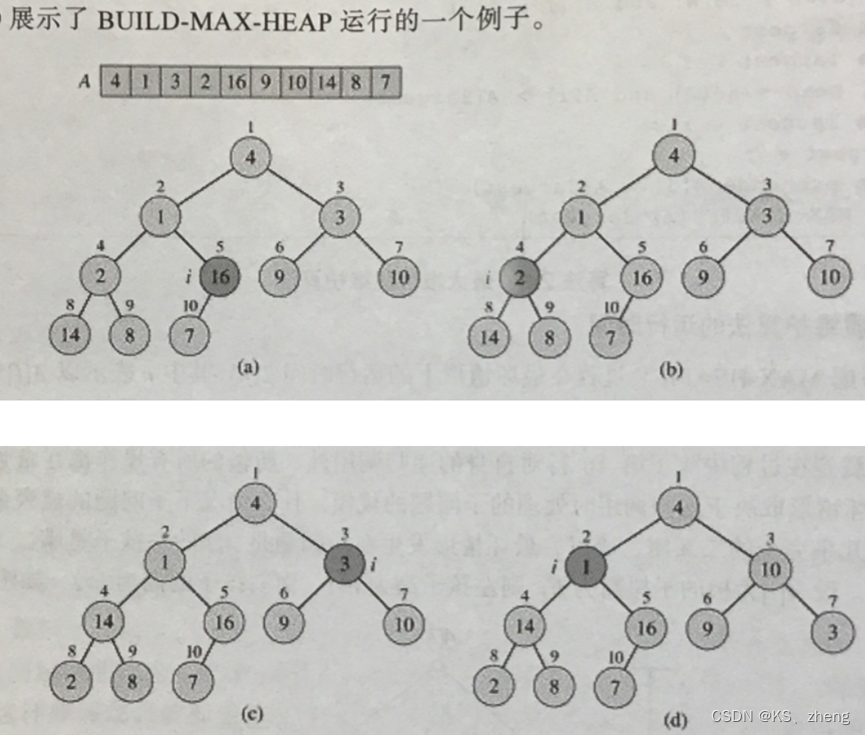
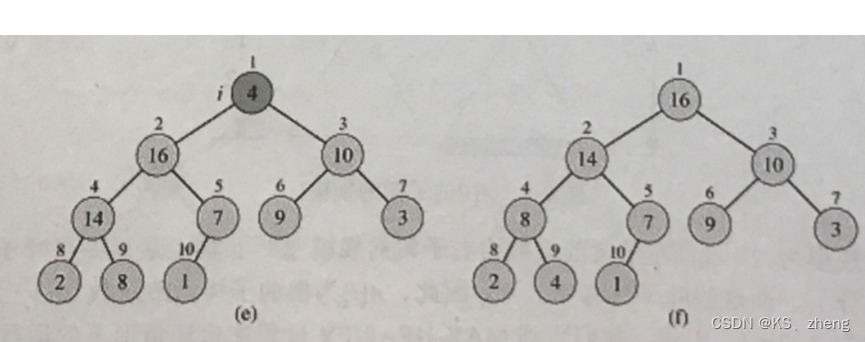
利用MAX-HEAPIFY通过自底向上的方式将数组A[1…n]转换成一个最大堆。由于子数组A[(n/2)+1…n]的每一个元素都没有左右孩子，所以都是树的叶子，因此每一个均构成一个单元素堆。过程BUILD-MAX-HEAP检测树种的其余节点并对每个节点运行MAX-HEAPIFY

BUILD-MAX-HEAP(A)
	for i <- (A.length/2) downto 1
		do MAX-HEAPIFY(A,i)

2.归并排序

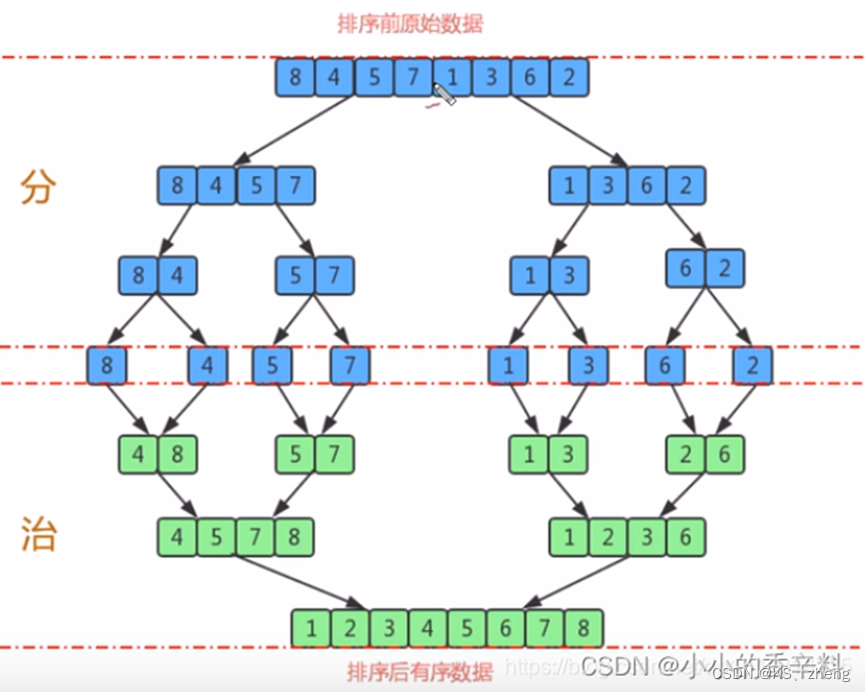
分：把一个未排序的序列从中间分割成2部分，再把2部分分成4部分，依次分割下去，直到分割成一个一个的数据
治，合：通过比较，再把这些数据两两归并到一起，使之有序。要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

代码：

void merge(int low,int mid,int high)//合并函数
{
    int i = low,j = mid + 1,k = low;//i、j指向需要合并的两个序列的首位置
    while (i <= mid && j <= high)//i、j指针都不超过合并序列的最后位置
    {
        //将较小数存储在temp之中,并且后移指针
        if (num[i] < num[j]) tem[k++] = num[i++];
        else tem[k++] = num[j++];
    }
    while (i <= mid) tem[k++] = num[i++];//左半序列还有元素
    while (j <= high) tem[k++] = num[j++];//右半序列还有元素
    for (int i = low;i <= high;i++) num[i] = tem[i];//拷贝元素
}

void merge_sort(int l,int r)//递归设计:排序函数
{
    if (l >= r) return;//递归出口:分解至一个数
    int mid = (l + r) / 2;
    merge_sort(l,mid);//归并排序左半序列
    merge_sort(mid + 1,r);//归并排序右半序列
    merge(l,mid,r);//将左右合并
}

时间复杂度

T(N) = 2T(N/2) + O(N)= O(NlogN)

将规模为 N 的原问题分解成两个规模 N/2 的两个子问题，合并这两个子问题的代价是O(N)

3.快速排序

基本思想

用首元素x作划分标准，将输入数组A划分成不超过x的元素构成的数组AL大于x的元素构成的数组AR。其中AL, AR从左到右存放在数组A的位置。递归地对子问题AL和AR进行排序，直到子问题规模为1时停止.。

实现原理

1、设置两个变量 i、j，排序开始时：i = 1，j = n
2、找基准位置，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面，默认序列的第一个数为基准元素，假设为key，先j从右往左试探，直a[j] < key就停止试探，i从左往右试探，直到a[i] > key就停止试探，如果i < j，就交a[j]与a[i]；如果i与j相遇，则i或j上的元素与基准元素交换，则这一轮排序结束。时，基准元素将序列一分为二
3、递归调用分界点前和分界点后的子数组排序，最终就会得到排序好的数组

例如：6，2，7，3，9，8对这6个数进行从小到大排序
初始时，设数组的第一个元素6为基准，用i指向数组首元素，用j指向数组的最后一个元素，开始扫描。指针j从后往前扫描，直到扫描到一个小于基准6的元素之后，停下。指针i从前往后扫描，直到扫描到一个大于基准6的元素之后，停下。

在达到上图状态的时候，交换元素位置。

j指针继续向左试探，然后指针i、j相遇，此时，交换i、j指向的元素与基准元素的位置.至此，第一趟排序结束。基准6左边的元素均小于6，右边的元素均大于6

对上图中元素6左边的部分进行快速排序。首先指针i指向3，指针j指向2，j先从右往左试探，会发现2 < 3，故直接停下。然后i从左往右试探，发现i、j指针重合。故交换元素位置，如下图。

同理，再对6右边的部分快速排序。首先指针i指向7，指针j指向8，j先从右往左试探，查到比7小的元素，一直走到7的位置停下。发现i、j指针重合。故下一步继续快速排序9、8两个元素。最后得到一个递增序列。

代码：

void quick_sort(int l,int r)//对第l个元素到第r个元素进行排序
{
    if (l >= r) return;
    int temp = a[l];//保存基准
    int i = l,j = r;
    while (i != j)
    {
        while (a[j] >= temp && i < j) j--;//j指针从右往左试探
        while (a[i] <= temp && i < j) i++;//i指针从左往右试探
        if (i < j) swap(a[i],a[j]);//当i、j指针都停下后,交换元素位置
    }
    a[l] = a[i];//i == j退出循环,与基准元素交换位置
    a[i] = temp;//第一次快排结束,基准元素更新为temp,基准位置更新为i,再继续排序
    quick_sort(l,i - 1);//对基准左边快速排序
    quick_sort(i + 1,r);//对基准右边快速排序
}

时间按复杂度：
最好情况：每一次划分，AL 与AR 总是均衡的在两边，首元素最终落到中间。那么子问题就变成了原问题的一半的元素数量(但是有两个子问题)。

T(n)=2T(n/2)+n-1=Θ(nlogn)

最坏情况：每次划分，首元素依然是在首元素，它是最小的（或者是最大的），下次划分也是同样的结果。这种情况下，是最坏的情况。子问题永远比上一个原问题只少了一个元素。并且每次都需要对n-1个元素进行遍历比较。

T(n)=T(n-1)+n-1=n(n-1)/2=O(n^2)

4.最大子数组

把数组A[1…n]分成两个相等大小的块：A[1…n/2]和A[n/2+1…n]，最大的子数组只可能出现在三种情况：

• A[1…n]的最大子数组和A[1…n/2]最大子数组相同；
• A[1…n]的最大子数组和A[n/2+1…n]最大子数组相同；
• A[1…n]的最大子数组跨过A[1…n/2]和A[n/2+1…n] ；

前两种情况的求法和整体的求法是一样的，因此递归求得。
第三种，我们可以采取的方法也比较简单，沿着第n/2向左搜索，直到左边界，找到最大的和maxleft，以及沿着第n/2+1向右搜索找到最大和maxright，那么总的最大和就是maxleft+maxright。 而数组A的最大子数组和就是这三种情况中最大的一个。

代码：

int maxSubArray(int *A,int l,int r) 
{
    if l<r do
        mid = (l+r)/2;
        ml = maxSubArray(A,l,mid); //分治
        mr = maxSubArray(A,mid+1,r);
        for i=mid downto l do
            search maxleft;
        for i=mid+1 to r do
            search maxright;
        return max(ml,mr,maxleft+maxright); //归并
        then //递归出口
            return A[l];
}

时间复杂度

T(n)=2T(n/2)+ Θ(n)=O(nlog n)

滴答

提示：本文是对互联网上搜集内容的一些体会，侵权请联系。