数论跪了三天。。
这个题不难得到(n+d)%23=p; (n+d)%28=e; (n+d)%33=i
如何求解?
首先介绍一个所谓“逆”的概念。
给定整数a,有(a,m)=1,称ax=1(mod m)的一个解叫做a模m的逆。
下面给出求逆的程序。
#include <iostream>
#include <math.h>
using namespace std;
typedef long long LL;
void gcd(LL a, LL b, LL &d, LL &x, LL &y)
{
if(!b)
{
d = a, x = 1, y = 0;
}
else
{
gcd(b, a %b, d, y, x);
y -= x * (a/b);
}
}
LL inv(LL a, LL n)
{
LL d, x, y;
gcd(a,n,d,x,y);
return d == 1 ? (x + n) % n : -1;
}
int main()
{
LL a, m;
while(cin>> a>>m)
{
cout << inv(a, m) <<endl;
}
}
比如9模31的逆是7。可输入9 31,得出7。
“中国剩余定理”
http://en.wikipedia.org/wiki/Chinese_remainder_theorem
百度百科介绍的就是一坨屎,看都别看!
言归正传,如何解这个方程:
(n+d)%23=p;(n+d)%28=e;(n+d)%33=i;
大家看到了,都是让它的余数变成1(为了求逆)。“大衍求一术”。
----------------------------------------------------------------------
Finding the solution with basic algebra and modular arithmetic
For example, consider the problem of finding an integer x such that
A brute-force approach converts these congruences into sets and writes the elements out to the product of 3×4×5 = 60 (the solutions modulo 60 for each congruence):
- x ∈ {2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38, 41, 44, 47, 50, 53, 56, 59, …}
- x ∈ {3, 7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, …}
- x ∈ {1, 6, 11, 16, 21, 26, 31, 36, 41, 46, 51, 56, …}
To find an x that satisfies all three congruences, intersect the three sets to get:
- x ∈ {11, …}
Which can be expressed as
Another way to find a solution is with basic algebra, modular arithmetic, and stepwise substitution.
We start by translating these congruences into equations for some t, s, and u:
- Equation 1:

- Equation 2:

- Equation 3:

Start by substituting the x from equation 1 into congruence 2:
meaning that  for some integer s.
for some integer s.
Plug t into equation 1:
Plug this x into congruence 3:
Casting out fives, we get
meaning that
for some integer u.
Finally,
So, we have solutions 11, 71, 131, 191, …
Notice that 60 = lcm(3,4,5). If the moduli are pairwise coprime (as they are in this example), the solutions will be congruent modulo their product.
A constructive algorithm to find the solution
The following algorithm only applies if the  's are pairwise coprime. (For simultaneous congruences when the moduli are not pairwise coprime, themethod of successive substitution can often yield solutions.)
's are pairwise coprime. (For simultaneous congruences when the moduli are not pairwise coprime, themethod of successive substitution can often yield solutions.)
Suppose, as above, that a solution is required for the system of congruences:
Again, to begin, the product 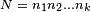 is defined. Then a solution x can be found as follows.
is defined. Then a solution x can be found as follows.
For each i the integers  and
and  are coprime. Using the extended Euclidean algorithm we can find integers
are coprime. Using the extended Euclidean algorithm we can find integers 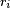 and
and  such that
such that  . Then, choosing the label
. Then, choosing the label  , the above expression becomes:
, the above expression becomes:
Consider  . The above equation guarantees that its remainder, when divided by
. The above equation guarantees that its remainder, when divided by  , must be 1. On the other hand, since it is formed as
, must be 1. On the other hand, since it is formed as 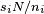 , the presence of N guarantees a remainder of zero when divided by any
, the presence of N guarantees a remainder of zero when divided by any  when
when  .
.
Because of this, and the multiplication rules allowed in congruences, one solution to the system of simultaneous congruences is:
For example, consider the problem of finding an integer x such that
Using the extended Euclidean algorithm, for x modulo 3 and 20 [4×5], we find (−13) × 3 + 2 × 20 = 1; i.e., e1 = 40. For x modulo 4 and 15 [3×5], we get (−11) × 4 + 3 × 15 = 1, i.e. e2 = 45. Finally, for x modulo 5 and 12 [3×4], we get 5 × 5 + (−2) × 12 = 1, i.e. e3 = −24. A solution x is therefore 2 × 40 + 3 × 45 + 1 × (−24) = 191. All other solutions are congruent to 191 modulo 60, [3 × 4 × 5 = 60], which means they are all congruent to 11 modulo 60.
Note: There are multiple implementations of the extended Euclidean algorithm which will yield different sets of 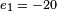 ,
, 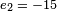 , and
, and 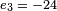 . These sets however will produce the same solution; i.e., (−20)2 + (−15)3 + (−24)1 = −109 = 11 modulo 60.
. These sets however will produce the same solution; i.e., (−20)2 + (−15)3 + (−24)1 = −109 = 11 modulo 60.
----------------------------------------------------------------------
那么,程序很简单
注意一点,如果直接对21252取余,再减去d,可能会出现负数的情况。
#include<iostream>
using namespace std;
int main()
{
int p, e, i, d;
int time = 1;
while (cin >> p >> e >> i >> d)
{
if (p == -1 && e == -1 && i == -1 && d == -1)
break;
int n = (5544 * p + 14421 * e + 1288 * i - d + 21252) % 21252;
if (n == 0)
n = 21252;
cout << "Case " << time++ << ": the next triple peak occurs in " << n << " days." << endl;
}
}请试着解下列同余方程组作为练习








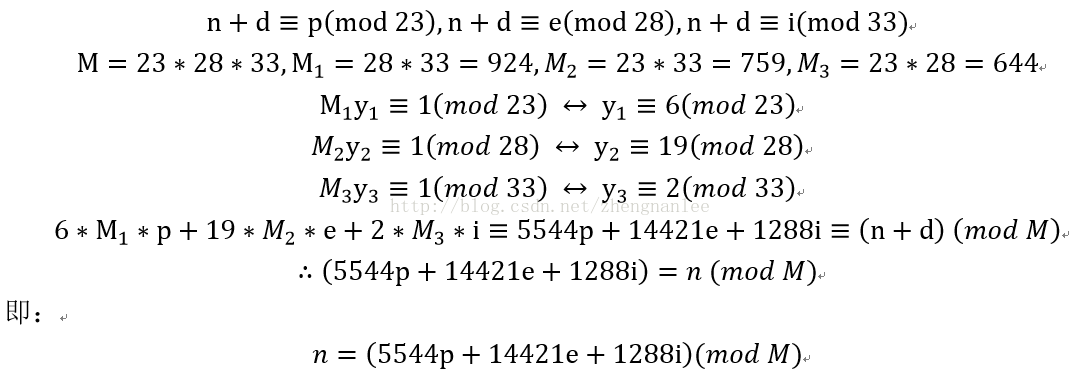

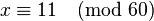
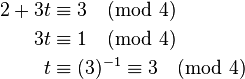
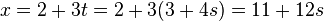

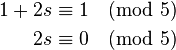




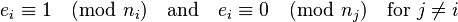
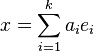

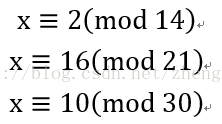














 723
723

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








