通俗易懂理解几何光学（五）光线的光路计算及像差理论

概述

在几何光学中，我们知道一个物点经单折射球面后不能够完善成像，但若把光线限制在近轴范围内,则可认为物点成理想的像点，但若高次项不可忽略，就会出现不完善成像的情况。

实际光学系统都有一定大小的相对孔径和视场，远远超出近轴区所限定的范围。
与近轴区成像比较必然在成像位置和像的大小方面存在一定的差异，被称为像差。

像差——实际像与理想象之间的偏差。

对于成像光学系统，像差是有害的，而没有像差的光学系统是不存在的。不可能完全消除像差。根据系统的作用和接收器的特性，把像差校正到某一公差范围内。

像差分类

1.几何像差

A.单色像差
轴上点像差：球差
轴外点像差：
彗差（正弦差）
像散
场曲
畸变

B.色差
位置色差
倍率色差

2.波像差：实际波面与理想球面波的偏差（基于波动光学）

消像差基本原则
对接收器的最灵敏谱线校正单色像差；对接收波段范围两边缘附近的谱线校正色差。

目视光学系统：对D光（λ=589.3nm）或e光（ λ=546.1nm ）校正单色像差；对F光（λ=486.1nm）和C光（λ=656.3nm）校正色差
普通照相系统： F光校正单色像差。D光和G’光（λ=434.1nm）校正色差
近红外光学系统

光线的光路计算

光路计算

已知条件
1.光学系统的结构参数（r, d, n）
2.物体的位置和大小
3.入瞳的位置和大小

拟解决问题
1.理想像的位置和大小
2.实际像的位置和大小

三类主要光线

子午面内的光线光路计算
沿轴外点主光线的细光束光路计算
子午面外光线或空间光线的计算（复杂）

对于小视场的光学系统，例如望远物镜和显微物镜等，只要求校正与孔径有关的像差，所以只需计算上述第一种光线。对大孔径、大视场的光学系统，如照相物镜等，要求校正所有像差，所以需要计算上述三种光线。

单色像差

球差

物距L为定值时，像距L′是U或h的函数。
轴上点A发出的同心光束经系统折射后，不同孔径角U的光线与光轴相交于不同点，相对于理想像点的位置有不同的偏离——球[面像]差。

什么是球差
接收屏在空间沿着主光轴移动，在任何位置都不能成几何点，接收到的都是圆形的弥散斑，位置不同，弥散斑的直径也不同。

影响因素:
是孔径(h或U)的函数。
与f′, D/f′, n, r, 透镜形状有关。

校正
大部分光学系统只能对某一高度（孔径角）校正球差，一般是对边缘带校正球差，即δLm′ = 0
δLm′ < 0，球差欠校正
δLm′ > 0，球差过校正

校正
配曲（利用透镜形状与球差的关系消除单透镜的像差）
透镜的纵向球差与透镜的折射率nL、曲率半径r1, r2有关。
透镜焦距f′也是nL, r1, r2这三个参量的函数。
对给定的nL，同样焦距f′的透镜可以有不同的曲率比r1/r2，选择某个比值，使球差值达到最小。

校正
组合（正负透镜的组合）
单正透镜的球差是负的；单负透镜的球差是正的。
正、负两个透镜粘合起来，组成一个复合透镜，可使某个高度h上的球差完全抵消。

最简单方法
在透镜前加一个光阑，让近轴光线通过。

说明：
1.球差是轴上点唯一的单色像差。
2.任何光学系统都必须校正球差。
球差使得像平面上的像由弥散斑组成，不能反映物体的细节。
3.不论采取什么措施或多复杂的系统，一般只能对某一孔径环带消除球差，而不能同时对各种孔径角的环带消除球差，总有一定的剩余球差。

正弦差和彗差

设轴上物点A→A’能以任意宽光束完善成像，则垂轴方向的近轴轴外点B→B’也能以宽光束完善成像需满足的条件称正弦条件。

$nysinU=n^{{}^{\prime }}{y}^{{}^{\prime }}sin{U}^{{}^{\prime }}$

当物距为无穷远时，经公式变换，可将正弦条件写成
$f^{{}^{\prime }}=h_1/sin{U}^{{}^{\prime }}$

正弦差表征光学系统不满足等晕条件的程度。当正弦差不为零时，轴外点存在彗差。

子午面与弧矢面
子午面：物点发出的主光线和光轴所决定的平面
子午光线：位于子午面内的光线
弧矢面：通过主光线并垂直于子午面的平面
弧矢光线：弧矢面内的光线

什么是彗差
轴外物点发出的粗光束，经系统后所成的像对主光线失去对称性，靠近主光线的细光束交于主光线形成亮点，远离主光线的不同孔径的光束形成远离主光线的不同圆环。轴外物点在理想像面上形成如同彗星状的光斑，这种成像缺陷称为彗差。

子午彗差

子午面内，某孔径上、下光线对经系统后的交点BT′到主光线的垂轴距离，KT′。

子午光线经系统成像仍在子午面内。
由于系统像差的存在，对称于主光线两侧的子午光线对a、b，经系统后，交点不在主光线上，也不交在理想像面上。

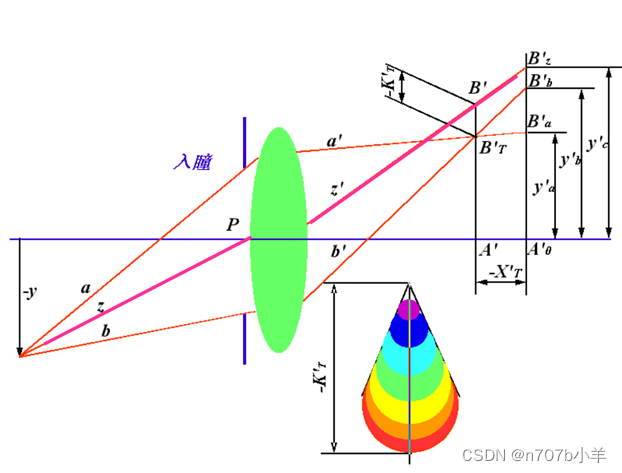
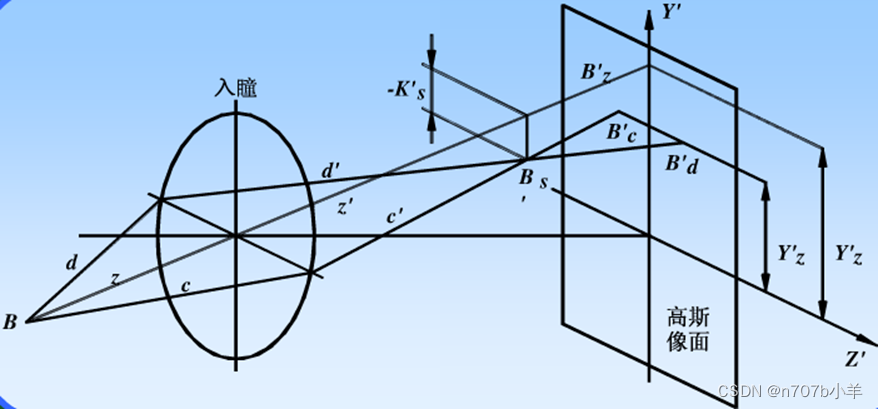
弧矢彗差

弧矢面内，某孔径前、后光线对经系统后的交点BS′到主光线的垂轴距离，KS′。

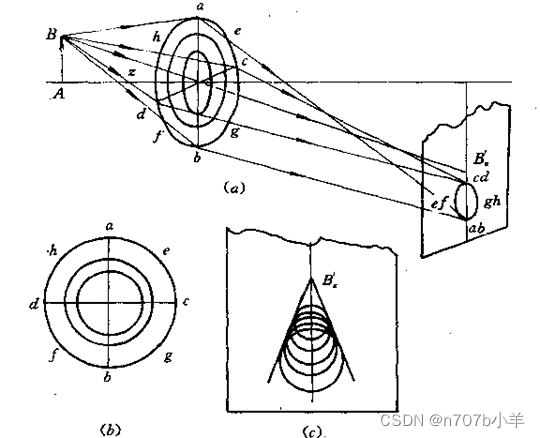
形状及大小
将入瞳看作由无数个大小不等的圆环组成，由轴外物点发出的所有通过这些圆环的圆锥面光束，经系统后在理想像面上截得大小不等、形状不一、并在垂轴方向上相互错开的封闭曲线，最终叠加成一个形状复杂、对称于子午面的弥散斑。

弥散斑形状像彗星，从中心到边缘拖着一个由细到粗的尾巴，首端明亮、清晰，尾端宽大、暗淡、模糊。
正彗差（KT′ > 0）
负彗差（KT′ < 0）

影响因素
彗差的大小与孔径(h/U)和视场(y/⍵)有关。

对给定的离轴物点，成像光束越大，彗差越大。
物点离光轴越远，彗差越大。

彗差与透镜的形状有关。

配曲
适当选取透镜的曲率半径（形状）。
入瞳位置
入瞳位于单折射球面球心时，不产生彗差；入瞳偏离球心越远，彗差越大。

采用对称结构
孔径光阑位于系统中央，垂轴放大率β = -1。
孔径光阑前部和后部产生的彗差大小相等、符号相反，相互补偿。

像散

若把光阑缩到无限小，只允许沿主光线的无限细光束通过，则彗差不存在，但是有细光束的像散和场曲存在。

什么是像散
轴外B点发出的细光束在折射面上所截得的曲面不是一个对称的回转曲面，它在不同截面方向上有不同的曲率，并在子午和弧矢这两个相互垂直的截面方向上具有最大或最小的曲率。

子午和弧矢面上的细光束，虽然各自能会聚于主光线上的一点，但相互并不重合。子午像点和弧矢像点分开的距离称为像散。

像散曲面为旋转抛物面。

物体由线条组成，经系统后
在子午像面上，这些线条在水平方向很清晰，而垂直方向则看上去是模糊的；
在弧矢像面上，这些线条在垂直方向清晰聚焦，而水平分量则显得模糊。
在有像散的情况下，接收器在像方找不到同时能让各个方向的线条都清晰成像的单一像面位置。

影响因素
像散与视场(y或⍵)有关，与孔径无关。
视场越大，像散越大；
即使孔阑很小，在子午和弧矢方向仍然无法同时获得清晰像。
与光阑位置有关。

校正
控制视场大小。
正负透镜像散相反，胶合后可消除。
对于单折射面，合理确定孔阑位置（光阑在球心），使子午像面和弧矢像面两个抛物面重合为一个抛物面P，这个面称为Pettzval曲面，可消除像散。

场曲

什么是场曲
轴外物体不同视场的各点以细光束成像，具有不同的像散值，因此一个平面物体形成两个像面（子午像面与弧矢像面）。
轴上物点无像散，子午像面与弧矢像面在视场中心重合且与理想像面相切。
一个平面垂轴物体形成两个弯曲的像面，这种成像缺陷称为场曲。

用弯曲像面与理想像面的轴向距离来度量场曲。
子午场曲$x_t^{{}^{\prime }}=l_t^{{}^{\prime }}-x^{{}^{\prime }}$
弧矢场曲$x_s^{{}^{\prime }}=l_s^{{}^{\prime }}-l^{{}^{\prime }}$
场曲的效果
不论像面在任何平面位置，像总是一部分清晰，一部分不清晰。

影响因素
与物体视场(y或⍵)有关；
与光阑位置有关。

校正
控制视场大小
正负透镜分离的组合系统，复杂化系统
将探测器面弯曲以适应场曲
大幅航空相机

畸变

理想光学系统中，物、像共轭面上的垂轴放大率为常数，像与物总是相似的。
实际光学系统中，只有在近轴区域才有这样的性质。一般情况下，一对共轭面上的放大率并不是常数，随视场的增大而变化，即轴上物点与视场边缘具有不同的放大率，物和像因此不再完全相似，这种像对物的变形像差称为畸变。
畸变仅是像的变形，不影响像的清晰度。

系统对共轭面上不同高度的物体有不同垂轴放大率。
β不是常数，而是物高y的函数。

什么是畸变
绝对畸变——主光线像点高度与理想像点高度之差

相对畸变——绝对畸变与理想像高的比值
对应于直线像的弯曲度——线长度/弯曲半径。弯曲度小于4%时人眼无感觉。

分类
正畸变（枕形畸变）
边缘放大率 > 中央放大率
负畸变（桶形畸变）
边缘放大率 < 中央放大率

影响因素
畸变与视场(y或⍵)有关，与孔径无关。
畸变与孔径光阑位置有关。

校正
对于单个折射面，将孔径光阑设在球心处，不产生畸变。

对于单个薄透镜或薄透镜组，当孔径光阑与之重合时，不产生畸变。

孔径光阑后移——正畸变

孔径光阑前移——负畸变

β = -1的对称光学系统，光阑位于系统中央，前后部分的畸变大小相等、符号相反，自动校正。

色差

通常情况下，物体以复色光（例如白光）成像，光学材料对不同波长的谱线有不同的折射率。
透镜焦距取决于表面的曲率半径和材料折射率，当曲率半径确定后，焦距随折射率而变化。
当白光经过光学系统时，系统对不同波长有不同的焦距，各谱线将形成各自的像点，导致一个物点对应许多不同的像点位置和放大倍率，这种差异称为色差。
可见光范围内，用F光（蓝光）和C光（红光）的差异表示色差。

位置色差

同一透镜对不同波长的色光成像的焦距不同。
物距一定，焦距不同像距就不同，一个物点形成很多像点。

位置色差——轴上物点以复色光束成像时的像差，也称为轴向色差。
一般在0.707带消色差。

消色差后，不同孔径的光束仍然有不同的位置色差。
取若干孔径系数，对F和C光分别求得各个孔径时的像方截距，作出各自的球差曲线，同时绘出主色光（D光）的球差曲线。

注：理想像点的位置一般指的D光近轴区所成像点位置，C, D, F光的球差曲线均是针对该像点进行计算

这三条球差曲线可以同时直观地反映出几种像差：
各单色光的球差随孔径的变化；
位置色差随孔径的变化；
球差随色光的变化（色球差）；
二级光谱（ΔLFCDʹ）。

三条曲线在横轴上的交点代表了三种色光各自的理想像点，也反映了近轴的位置色差

在0.707带校正色差之后，边缘带色差ΔLFC′和近轴色差ΔlFC′并不相等，两者之差称为色球差，反应球差的色变化。

当0.707带消色差后，F光和C光的交点与D光像点位置一般并不重合，其距离称为二级光谱，用ΔLFCD′表示。

影响因素
与孔径(h或U)有关；
与透镜材料有关（与光焦度成正比，与阿贝常数成反比）。
校正
正、负透镜胶合（光焦度符号相反）

倍率色差

倍率色差严重时，物体的像有彩色边缘，即各种色光的轴外像点不重合。
倍率色差将破坏轴外点像的清晰度，造成白色像的模糊。

对轴外点，不同色光的焦距不等时，垂轴放大率也不相等，因而有不同像高

F光与C光主光线的像点高度之差，在参考像面（D光的像面）上度量，ΔYFC′或δyFC′。

倍率色差严重时，物体的像有彩色边缘，即各种色光的轴外像点不重合。
倍率色差将破坏轴外点像的清晰度，造成白色像的模糊。

影响因素
与视场(y或⍵)有关；
与光阑位置有关。
校正
选择光阑位置（参考畸变部分）；
β = -1的对称性结构系统；
有一定空气间隔的双薄透镜组合（双分离），通过调节空气间隔来校正。

波像差

适用于高像质要求的光学系统。
光线——波面的法线
理想波面——在理想成像的情况下，和理想像点对应的波面
波像差——实际波面与理想波面之间的光程差
当系统最大波像差＜λ/4，成像质量好；若＜λ/10，其成像是完善的。