算法：如何在内存中存储一个图呢？

OceanStar的学习笔记

已于 2022-08-03 16:39:51 修改

阅读量809

点赞数

分类专栏：算法与数据结构文章标签：算法

于 2022-01-12 16:49:00 首次发布

原文链接：https://mp.weixin.qq.com/s?__biz=MzIxMjE5MTE1Nw%3D%3D&chksm=8c99e609bbee6f1fb0df2fb60edb8fba5166b49ef200ab8fb3af4ff144b3f96b283a34ff776c&idx=2&mid=2653197523&scene=21&sn=893c01a31446d3c479c312836ae83819#wechat_redirect

版权

算法与数据结构专栏收录该内容

1135 篇文章

订阅专栏

图的表示

图在内存中的存储方式有很多种，包括邻接矩阵、邻接表、逆邻接表、十字链表等

拥有n个顶点的图，它所包含的连接数量最多是n(n-1)个

邻接矩阵

我们知道，数据结构有两种表示方式：

数组
链表

而图的数组表示就叫做邻接矩阵表示法，那么怎么用数组表示一个图呢？

首先，我们需要一个一维数组，里面存储了图的所有顶点信息。
然后，我们需要一个二维数组，用来描述边（边表示顶点和顶点之间的关系的，所以必须是二维数组）（这个二维矩阵就叫做邻接矩阵）

那么，这些数组应该申请多大呢？假设有n个顶点

那么一维数组至少应该是n
二维数组需要是一个n * n的方阵

无向图

我们先来看无向图的矩阵表示：
在这里插入图片描述

可以看到，当前图有四个顶点，所以申请了两个数组：

顶点数组为 $vertex[4]={V0,V1,V2,V3}$
边数组 $A [4] [4]$
- 顶点0和顶点1之间有边关联，那么矩阵中的元素A[0][1]与A[1][0]的值就是1
- 顶点1和顶点3之间没有边关联，那么矩阵中的元素A[1][3]与A[3][1]的值就是0

从图中我们可以注意到：

邻接矩阵从左上到右下的一条对角线，其上的元素值必然是0，因为任何一个顶点与它子树是没有连接的。
这是一个对称矩阵：
- 所谓对称矩阵就是n阶矩阵的元素满足 $a [i] [j] = a [j] [i] (0 <= i, j <= n)$ 。即从矩阵的左上角到右下角的主对角线为轴，右上角的元与左下角相对应的元全都是相等的。
- 无向图对应的矩阵一定是一个对称矩阵。为什么呢？V0和V1有关联，那么V1和V0也必定有关联，因此A[0][1]和A[1][0]的值一定相等

在这里插入图片描述

无向图的数组存储主要有以下特性：

顶点数组长度为0的顶点数目n。边数组为 $n * n$ 的二维数组
边数组中， $A [i] [j] = 1$ 表示顶点i和顶点j邻接， $A [i] [j] = 0$ 代表顶点i与顶点j不邻接
在无向图中，由于边是无向边，因此顶点的邻接关系是对称的，边数组为对称二维数组
顶点与自身之间并未邻接关系（自己和自己不能邻接），因此边数组的对角线上的元素均为0
顶点的度即为顶点所在的行或者列1的数目。例如：顶点V2的度为3，则V2所在行和列中的1的数目为3。

有向图

普通有向图的邻接矩阵

在这里插入图片描述
可以看到，当前图有四个顶点，所以申请了两个数组：

顶点数组为 $vertex[4]={V0,V1,V2,V3}$
边数组 $A [4] [4]$
- 顶点0和顶点1之间有边关联，那么矩阵中的元素A[0][1]的值就是1
- 顶点1和顶点0之间有边关联，那么矩阵中的元素A[1][0]的值就是1
- 顶点0和顶点3之间有边关联，那么矩阵中的元素A[0][3]的值就是1
- 顶点3和顶点0之间没有边关联，那么矩阵中的元素A[3][0]的值就是0

可以看出：

有向图不再是一个对称矩阵。从V0可以到底V1，从V1却未必能到底V0，因此A[0][1]和A[1][0]的值不一定相等。
有向图有个出度和入度的概念。比如对应顶点1来说：
- 入度就是第1列各数之和，为1
- 出度就是第1行各数之和，为2

带权图的邻接矩阵

带权图中的每一条边上带有权值，邻接矩阵中的值则为权值，当两个顶点之间没有弧时，则用无穷大表示。

在这里插入图片描述

有向图的数组存储主要有以下特性：

顶点数组长度为0的顶点数目n。边数组为 $n * n$ 的二维数组
边数组中，数组元素为1，即A[i][j] = 1,代表第i个顶点与第j个顶点邻接，且i为尾，j为头。 A[i][j] = 0代表顶点与顶点不邻接
在有向图中，由于边存在方向性，因此数组不一定为对称数组
对角线上元素为0
第i行中，1的数目代表第i个顶点的出度。例如：顶点V1的出度为2，则顶点V1所在行的1的数目为2。
第j列中，1的数目代表第j个顶点的入度。例如：V3的入度为1，则V3所在列中1的数目为1

优缺点

邻接矩阵的优点：简单直观，可以快速查到一个顶点和另一个顶点之间的关系

首先，邻接矩阵的存储方式简单、直接，因为基于数组，所以在获取两个顶点关系时，就非常高效
其次，用邻接矩阵存储图的另一个好处是方便计算。这是因为，用邻接矩阵的方式存储图，可以将很多图的运算转换成矩阵之间的运算。

邻接矩阵的缺点：占用了太多空间。为什么这么说呢？

对于无向图来说，如果 $A [i] [j]$ 等于1，那 $A [j] [i]$ 也肯定等于1。实际上，我们只需要存储一个就可以了。也就是说，无向图的二维数组中，如果我们将其用对角线划分为上线两部分，那我们只需要利用上面或者下面这样一半的空间就足够了，另外一半就白白浪费掉了
再比如，如果一个图有1000个顶点，其中只有10个顶点之间有关联(这种情况叫做稀疏图)，却不得不建立一个1000*1000的二维数组，太浪费了
如下图，图中有 9 个顶点，边数为10，需要 9X9 的二维数组，而实际存储边信息空间只有10，造成空间浪费。

另外，有时两个点之间不止存在一条边，这时用邻接矩阵就无法同时表示两条以上的边。

小结

邻接矩阵的底层依赖一个二维数组。
对于无向图来说，如果顶点 $i$ 和顶点 $j$ 之间有边，我们就将 $A [i] [j]$ 和 $A [j] [i]$ 都标记为 $1$
对于有向图来说，如果顶点 $i$ 和顶点 $j$ 之间，有一条箭头从顶点 $i$ 指向顶点 $j$ 的边，那我们就将 $A [i] [j]$ 标记为 $1$ 。同理，如果有一条箭头从顶点 $j$ 指向顶点 $i$ 的边，我们就将 $A [j] [i]$ 标记为 $1$ 。
对于带权图，数组中就存储相应的权重。

在这里插入图片描述

邻接表

为了解决邻接矩阵占用空间的问题，提出了一种特殊的图存储方式，让每个节点拥有的数组大小刚好等于它所连接的边数，这就是邻接表。

邻接表存储是一种数组存储+链式存储相结合的存储方法。

我们申请一个一维数组来存储图的所有顶点（顶点也可以用单链表来存储，不过数组可以较容易地读取顶点信息，更加方便。）
然后用单链表来表示每个顶点与其他顶点之间的关系（由于邻接点的个数不确定，所以必须是单链表）
- 每个顶点都对应一条单链表，链表中存储的是与这个顶点相连接的其他顶点
- 对于有向表的邻接表存储方式，每个顶点对应的链表里面，存储的是指向的顶点。
- 对于无向图来说，也是类似的，不过，每个顶点的链表中存储的，是跟这个顶点有边相连的顶点

很明显，这种邻接表的存储方式，占用的空间比邻接矩阵要小很多。

注：图采用邻接表的方式表示时，其表示方法是不唯一的。这是因为在每个顶点对应的单链表中，各边节点的链接次序是可以任意的，取决于建立邻接表的算法以及边的输入次序。

怎么定义呢：

在数组中存储叫做头节点，头结点由两个域组成，分别指向链表中第一个顶点和存储Vi的名或其他信息。具体结构如下图，其中，data域中存储顶点相关信息，firstarc指向链表的第一个节点。：

在这里插入图片描述

链表中的节点称为表节点，共有三个域，具体结构见下图，其中adjvex存储与Vi邻接的点在图中的位置，nextarc存储下一条边或弧的结点，data存储与边或弧相关的信息如权值.。

在这里插入图片描述

无向图邻接表

在这里插入图片描述

以V0顶点为例，V0顶点的邻接顶点为V1、V2、V3，则可以创建3个表节点，表节点中adjvex分别存储V1、V2、V3的索引1、2、3

无向图的邻接表存储特性：

数组中头节点的数目为图的顶点数目。
链表的长度就是顶点的度。比如，V0顶点的度为3，则以V0为头节点的链表中表节点的数目为3

带权网络的邻接表

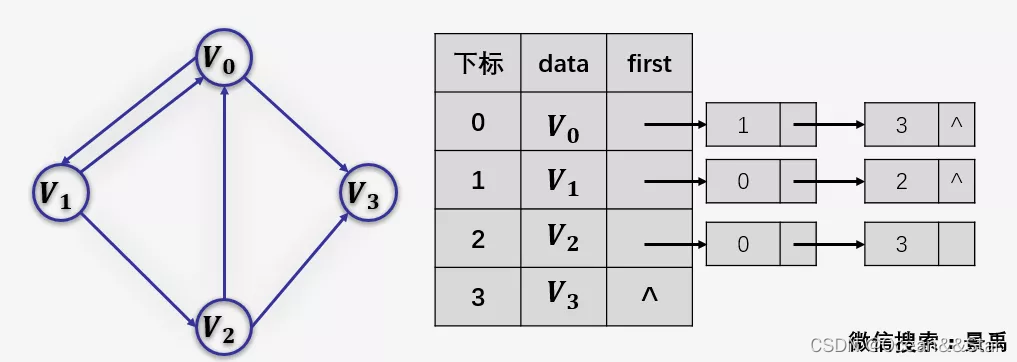
在这里插入图片描述

有向图邻接表

在这里插入图片描述

逆邻接表

假设我们有邻接表如下：

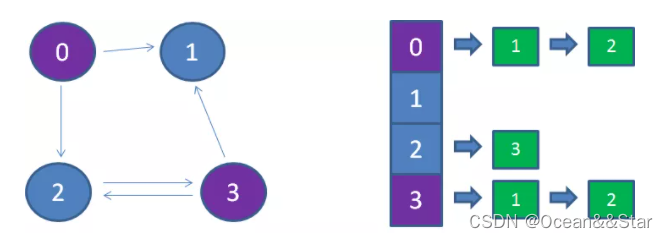
在这里插入图片描述

要想查出从顶点0能否到达顶点1，该怎么做呢？我们从顶点0开始，顺着链表的头节点从后遍历，看看后继的节点中是否存在顶点1.
要想查出顶点0能够到达的所有相邻节点，也很简单，从顶点0向后的所有链表节点，就是顶点0能够到达的相邻节点。

那么，要想查出有哪些节点能一步到达顶点1，又该怎么做呢？

这样就麻烦一些了，我们要遍历每一个顶点所在的链表，看看链表节点中是否包含节点1，最后发现顶点0和顶点3可以到达顶点1。

像这种逆向查找的麻烦，该如何解决呢？我们可以是用逆邻接表来解决。

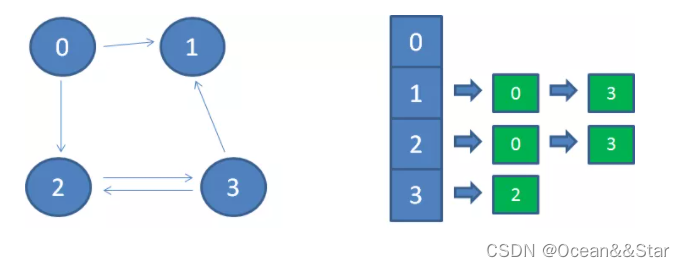
在这里插入图片描述
逆邻接表顾名思义，和邻接表是正好相反的。逆邻接表每一个顶点作为链表的头节点，后继节点所存储的是能够直接达到该顶点的相邻顶点。

这样一来，要想查出有哪些节点能一步到达顶点1就容易了，从顶点1向后的所有链表节点，就是能一步到达顶点1的节点。

在这里插入图片描述

因此，我们可以根据实际需求，选择使用邻接表还是逆邻接表。

问题是，一个图总是要维护正反两个邻接表，也太麻烦了。这时就出现了把邻接表和逆邻接表结合在一起的十字链表

十字链表

十字链表长什么样呢？用最直观的示意，是下面这样：

在这里插入图片描述
如图所示，十字链表的每一个顶点，都是两个链表的根节点，其中一个链表存储着该顶点能到达的相邻顶点，另一个链表存储着能到达该顶点的相邻节点。

不过，上图只是一个便于理解的示意图，我们没有必要把链表的节点都重复存储两次。在优化之后的十字链表中，链表的每一个节点不再是顶点，而是一条边，里面包含起止顶点的下标。

十字链表节点和边的对应关系，如下图所示：

在这里插入图片描述
因此，优化之后的十字链表，是下面这个样子：

在这里插入图片描述
图中每一条带有蓝色箭头的链表，存储着从顶点出发的边；每一条带有橙色箭头的链表，存储着进入顶点的边

怎么定义

顶点节点即为头节点，由3个域构成，具体形式如下：

在这里插入图片描述

边节点为链表节点，共有 5个域（info省略了），具体形式如下：

为了更直观地理解十字链表，我们可以先看一下邻接表与逆邻接表的表示：
在这里插入图片描述
十字链表的表示：

其中红色连接线与蓝色链接线分别代表邻接表表示与逆邻接表表示。

十字链表的好处就是因为把邻接表和逆邻接表整合在了一起，这样既容易找到以Vi为尾的弧，也容易找到以Vi为头的弧，因而容易求得顶点的出度和入度。

十字链表除了结构复杂一点外，其实创建图算法的时间复杂度是和邻接表相同的，因此，在有向图的应用中，十字链表也是非常好的数据结构模型。

邻接多重表

如果我们在无向图的应用中，关注的重点是顶点的话，那么邻接表是不错的选择，但如果我们更关注的是边的操作，比如对已经访问过的边做标记，或者删除某一条边等操作，邻接表的确显得不那么方便了（下图中删除红色边）。

在这里插入图片描述

邻接表对边的操作显然很不方便，因此，我们可以仿照十字链表的方式，对边表结构进行改装

邻接多重表仿照了十字链表的思想，对邻接链表的边表结点进行了改进：对于无向图而言，其每条边在邻接链表中都需要两个结点来表示，而邻接多重表正是对其进行优化，让同一条边只用一个结点表示即可。

重新定义的边结点结构如下图：

在这里插入图片描述
其中，ivex和jvex是指某条边依附的两个顶点在顶点表中的下标。 ilink指向依附顶点ivex的下一条边，jlink指向依附顶点jvex的下一条边。info存储边的相关信息。

重新定义的顶点结构如下图：

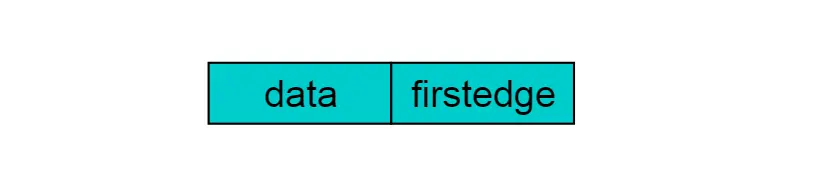
在这里插入图片描述

也就是说在邻接多重表里边，边表存放的是一条边，而不是一个顶点。
在这里插入图片描述

这样删除一条边就容易多了。

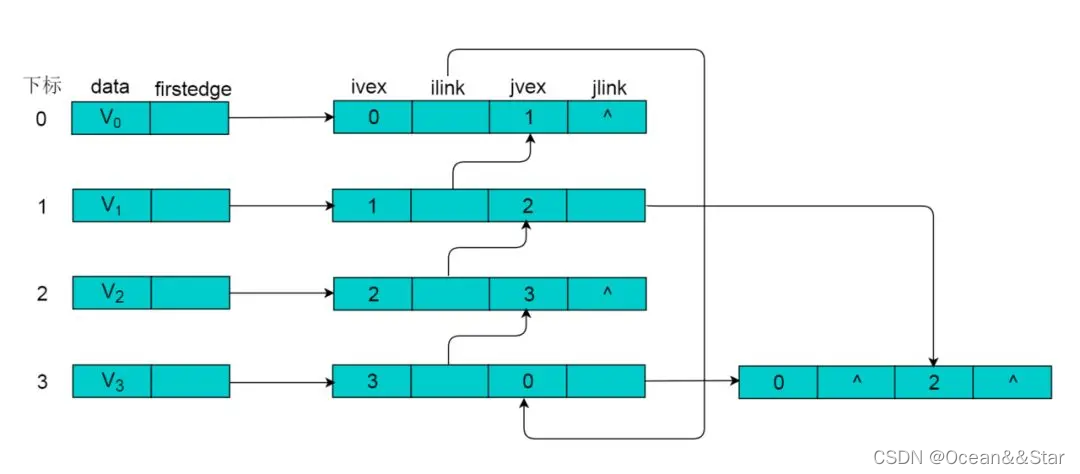
例子，采用邻接多重表存储下面无向图

在这里插入图片描述
以V0为例，顶点data域存储V0名称，firstedge指向(V0，V1)的边，边节点中的ilink指向依附V0顶点的下一条边(V0 , V3)，jlink指向依附V1顶点的下一条边(V1 , V2)，按照此方式建立邻接多重表：

在这里插入图片描述

边集数组

边集数组是由两个一维数组构成，一个是存储顶点的信息，另一个是存储边的信息，这个边数组每个数据元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成。

在这里插入图片描述

看个例子

利用两个数组分布存储顶点和边。
在这里插入图片描述

在这里插入图片描述

邻接矩阵

（1）我们先只考虑图顶点的信息：先用一个一维数组存储图的顶点。

对于G1，它的顶点用数组存储
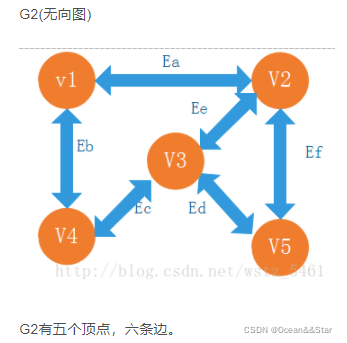
在这里插入图片描述
对于G2，它的顶点用数组存储

在这里插入图片描述

（2）我们再来考虑图的边。因为一条边连接两个顶点，为了描述这个关系，再利用一个二维数组来存储图的边。把二维数组看成是一个矩阵。

对于G1，它的边用二维数组

在这里插入图片描述
其中E[i][j]为1表示，从顶点v[i]到顶点v[j]有边（这是有方向的）

对于无向图G2,它的边也可以用二维数组来表示：
在这里插入图片描述
其中E[i][j]为1表示顶点V[i]与V[j]之间有边（没有方向），注意：这和有向图是不一样的，大家可以看到无向图的二维数组是关于对角线对称的。

这样通过一维数组来保存顶点数据信息，二维数组来表示两两顶点的边。就完成了对图形数据结构的存储

下面是一个无向图的实现：

/*GraphStruct.h
* 图的邻接矩阵存储方式，结构由顶点数量、边数量、顶点集合和边集合组成。
* 其中顶点集合一维数组，根据顶点的数量动态分配数组大小。
* 边集合是二维数组，根据顶点的数量来动态分配数组大小，对于无向图来说，该邻接矩阵是对称矩阵。
* 邻接矩阵比较适用于稠密图
*/
typedef char vertexType;
typedef int edgeType;
typedef struct GraphMatrix{

    int vertexNumber;            // 顶点数量
    int edgeNumber;                // 边的数量
    vertexType *vertex;            // 顶点集合，动态数组
    edgeType** edge;            // 边集合，二维动态数组

} GraphMatrix;

void GraphMatrix_create(GraphMatrix *g);

#include <stdio.h>
 #include <malloc.h>
#include"GraphStruct.h"

void GraphMatrix_create(GraphMatrix *g){
    printf("请分别输入图的顶点数量和边的数量，用空格隔开：");
    scanf("%d %d", &g->vertexNumber, &g->edgeNumber);
    g->vertex = (vertexType *)malloc(g->vertexNumber * sizeof(vertexType)); //为动态数组申请空间
    //二维动态数组申请空间
    g->edge =(edgeType**)malloc(g->vertexNumber * sizeof(edgeType*));
    for (int i = 0; i < g->vertexNumber; i++){
        g->edge[i] = (edgeType*)malloc(g->vertexNumber * sizeof(edgeType));
    }

    //初始化邻接矩阵的所有元素
    for (int i = 0; i < g->vertexNumber; ++i) {
        for (int j = 0; j < g->vertexNumber; ++j) {
            g->edge[i][j] = 0;
        }
    }
    
    //输入图的信息
    for (int k = 0; k < g->edgeNumber ; ++k) {
        int i, j;
        printf("请输入边(vi,vj)的下标, i和j，用空格隔开:");
        scanf("%d %d", &i, &j);
        g->edge[i][j] = 1;
        g->edge[j][i] = 1;
    }
    //输出图的信息
    printf("Your graph matrix is :\n");
    for (int i = 0; i < g->vertexNumber; i++){
        for (int j = 0; j < g->vertexNumber; j++){
            printf("%d\t", g->edge[i][j]);
        }
        printf("\n");
    }
}

int main()
{
    GraphMatrix *gm;
    gm = (GraphMatrix *)malloc(sizeof(GraphMatrix));
    GraphMatrix_create(gm);
    return 0;
}

在这里插入图片描述

邻接表

（1）我们依然先利用一维数组将图的订单存储起来

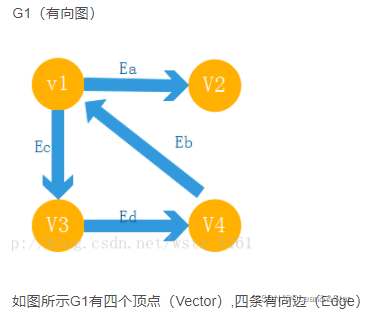
对于G1
在这里插入图片描述
先强调一下弧头和弧尾以及弧的概念：弧头和弧尾都是指顶点，在G1中，对于Ea来说V1是弧头，V2是弧尾

（2）再将图的边加进来

在这里插入图片描述

综上，对于边(i,j)，邻接表如下：
在这里插入图片描述

左边的节点称为顶点节点，其结构体包含顶点元素和指向第一条边的指针；右边的为边节点，结构体包含边的顶点对应的下标，和指向下一个边节点的指针。对于有权值的网图，只需要在边节点增加一个权值的成员变量即可。

typedef char vertexType;
typedef int edgeType;

typedef struct ListEdgeNode{
    int index;                    // 边的下标
    struct ListEdgeNode *next;            // 指向下一个节点的指针
}ListEdgeNode;

typedef struct ListVertexNode {
    vertexType vertex;            // 顶点
    ListEdgeNode *fistEdge;        // 指向第一条边
} ListVertexNode;

// GraphList是链接表的结构体，包含了顶点数，边数和顶点集，其中顶点集根据顶点个数分配内存空间。
typedef struct GraphList{
    int vertexNumber;            // 顶点的数量
    int edgeNumber;                // 边的数量
    ListVertexNode *vertex;        // 顶点集合，动态数组
}GraphList;

void GraphList_Create(GraphList *g){
    printf("请分别输入图的顶点数量和边的数量，用空格隔开：");
    scanf("%d %d", &g->vertexNumber, &g->edgeNumber);
    //为动态数组申请空间
    g->vertex = (ListVertexNode *)malloc(g->vertexNumber * sizeof(ListVertexNode));
    //初始化顶点指的第一条边
    for (int i = 0; i < g->edgeNumber; ++i) {
        g->vertex[i].fistEdge = NULL;
    }

    //输入图的信息
    ListEdgeNode *listEdgeNode;
    for (int j = 0; j < g->edgeNumber; ++j) {
        int i, v;
        printf("请输入边(vi,vj)的下标, i和j，用空格隔开:");
        scanf("%d%d", &i, &j);
        //始终将插入的节点放在顶点所指的一条边
        listEdgeNode = (ListEdgeNode *)malloc(sizeof(ListEdgeNode));
        listEdgeNode->index = j;
        listEdgeNode->next = g->vertex[i].fistEdge;
        g->vertex[i].fistEdge = listEdgeNode;

        listEdgeNode = (ListEdgeNode*)malloc(sizeof(ListEdgeNode));
        listEdgeNode->index = i;
        listEdgeNode->next = g->vertex[j].fistEdge;
        g->vertex[j].fistEdge = listEdgeNode;
    }


    //输出图的信息
    ListEdgeNode * node = NULL;
    for (int i = 0; i < g->vertexNumber; ++i) {
        if (g->vertex[i].fistEdge != NULL){
            node = g->vertex[i].fistEdge;
        }
        while (node != NULL){
            printf("%d --- %d\t", i, node->index);
            node = node->next;
        }
        printf("\n");
    }
}

int main()
{
    GraphList *gl;
    gl = (GraphList*)malloc(sizeof(GraphList));
    GraphList_Create(gl);
    return 0;
}

在这里插入图片描述

问题：如何存储社交网络中的好友关系

以”微博“为例。数据结构是为算法服务的，所以具体选择哪种存储方法，与其他支持的操作有关系。针对微博用户关系，假设我们需要支持下面这样几个操作：

判断用户 A 是否关注了用户 B；
判断用户 A 是否是用户 B 的粉丝；
用户 A 关注用户 B；
用户 A 取消关注用户 B；
根据用户名称的首字母排序，分页获取用户的粉丝列表；
根据用户名称的首字母排序，分页获取用户的关注列表。

关于如何存储一个图，主要有两种方法，邻接矩阵和邻接表。因为社交网络是一张稀疏图，使用邻接矩阵比较浪费存储空间。所以，这里我们采用邻接表来存储。

不过，仅用一个邻接表来存储这种有向图是不够的。我们取查找某个用户关注了哪些用户非常容易，但是如果想要知道某个用户被哪些用户关注了，也就是用户的粉丝列表，是非常困难的。

基于此，我们需要一个逆邻接表。

邻接表种存储用户的关注关系，逆邻接表存储用户的被关注关系
对应到图上，邻接表中，每个顶点的链表中，存储的就是这个顶点指向的顶点，逆邻接表中，每个顶点的链表中，存储的是指向这个顶点的顶点。
如果要查找某个用户关注了哪些用户，我们可以在邻接表中查找；如果要查找某个用户被哪些用户关注了，我们从逆邻接表中查找。

在这里插入图片描述
基础的邻接表不适合快速判断两个用户之间是否是关注和被关注的关系，所以我们选择改进版本，将邻接表的链表改为支持快速查找的动态数据结构。那应该选择哪种动态数据结构呢？红黑树、调表、有序动态数组还是散列表呢？

因为我们需要按照用户名称的首字母排序，分页来获取用户的粉丝链表或者关注列表，用跳表这种是最合适的。
这是因为，调表插入、删除、查找都非常高效，时间复杂度 $O (l o g n)$ ，空间复杂度上稍高，是 $O (n)$ 。最重要的是，跳表种存储的数据本来就是有序的，分页获取粉丝列表或者关注列表，就非常高效