算法：找到二叉树中符合搜索二叉树条件的最大拓扑结构

题目来源

• 牛客网

题目描述

给定一棵二叉树的头节点head，已知所有节点的值都不一样，返回其中最大的且符合搜索二叉树条件的最大拓扑结构的大小。

例如，二叉树如图：

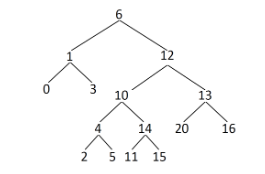
其中最大的且符合搜索二叉树条件的拓扑结构如图：

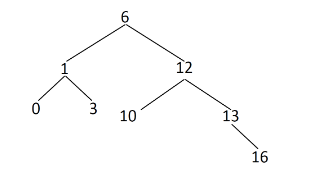
这个拓扑结构节点数为8，所以返回8。

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};


class Solution{
public:
    int bstTopoSize(TreeNode *head){
 
    }
};

题目解析

二叉树的节点数为N，时间复杂度为O(N^2)的方法

核心思路：把整个二叉树中每个节点都作为一次头结点，寻找以它为头结点的情况下的最大搜索二叉树的拓扑结构。其中最大的那个就是我们想要的结构。

算法用到了三层递归：

• 第一层递归：以各个节点为头结点的情况下来对比各种情况下的搜索二叉树的最大拓扑结构，并且不断的取最大值。最后返回的值就是整个二叉树中符合条件的最大值
• 第二次递归：以当前节点为头结点的情况下，寻找最大拓扑结构。如果一个节点不满足条件，则不再往其子节点寻找，否则，一直沿着子树往下寻找
• 第三层递归：判断当前节点是否可以作为这个拓扑结构的一部分。即从当前头节点出发，按照二叉搜索的方式移动。能找到当前节点，则返回true。不能则返回false。

三层递归的关系：

• 第一层递归需要用到什么？需要用到以各个节点为头节点的情况下的最大拓扑结构的节点数。这就是第二层递归。
• 而第二层递归需要用到什么？需要用到判断每个节点是否可以作为这个拓扑的一部分。这就是第三层递归。
• 而第三层递归就是最内层，从当前头节点开始不断往下递归寻找当前节点，来返回true或者false。

class Solution{
	 // 在以head为头结点的树中，用二叉搜索的方式能否找到节点node
    bool isBSTNode(TreeNode *head, TreeNode *node, int value){
        if(head == nullptr){
            return false;
        }
        if(head == node){
            return true;
        }
        
        return isBSTNode(head->val > value ? head->left : head->right, node, value);
    }
      /**
     * 在以head为头结点的树中，在拓扑结构以node为头结点的情况下，找最大拓扑
     *
     * @param head 整棵树的头结点
     * @param node 拓扑结构的头结点（也是当前正在考察的节点）
     * @return 最大拓扑包含的节点数量
     */
    int maxTop(TreeNode *head, TreeNode *node){
    	 // 先考查head 的孩子节点，调用isBSTNode考察这个孩子节点是否可以作为这个（以h为头结点的）拓扑的一部分。
        // 如果可以，则继续考查这个孩子节点的孩子节点，一直延伸下去。
        if(head != nullptr && node != nullptr && isBSTNode(head, node, node->val)){
        	 // 最大拓扑结构包含节点数量 = node的左子树的最大拓扑数量 + node的右子树的最大拓扑数量 + node本身
            return maxTop(head, node->left) + maxTop(head, node->right) + 1;
        }
        return 0;  // 当前节点不能作为整个拓扑的一部分延伸下去，故返回0
    }
public:
	  /**
     * 方法一：时间复杂度 O(n^2)
     * 只要遍历所有的二叉树节点，并在以每个节点为头节点的子树中都求一遍其中的最大拓扑结构，
     * 其中最大的那个就是我们想找的结构，它的大小就是返回值。
     */
    int bstTopoSize(TreeNode *head){
        if(head == nullptr){
            return 0;
        }
        
        int max = maxTop(head, head);  // 在以head为头结点的树中，在拓扑结构也以h为头结点的情况下，找最大拓扑
        max = std::max(bstTopoSize(head->left), max);
        max = std::max(bstTopoSize(head->right), max);
        return max;
    }
};

二叉树的节点数为N，时间复杂度为O(N)的方法。

主要是用到了一个重要的概念——拓扑贡献记录（2个值分别代表左、右子树可以贡献多少个节点）

递归的过程中不断更新这个拓扑贡献记录，对于当前头结点，左子树只需要不断的考察其右边界、右子树不断地考察其左边界。

从小树的记录整合成大树的记录，从而求出整棵树中符合搜索二叉树条件的最大拓扑的大小。

整个过程大体说来就是利用二叉树的后序遍历，对每个节点来说，首先生成其左孩子节点的记录，然后是右孩子节点的记录，接着把两组记录修改成以这个节点为头的拓扑贡献记录，并找出所有节点的最大拓扑结构中最大的那个。

举个例子，如下图，每个节点的都有被括号括起来的两个值

• 第一个值表示节点的左子树可以为当前头结点的拓扑贡献几个节点
• 第二个值代表节点的右子树可以为当前头结点的拓扑贡献几个节点

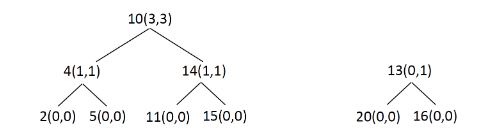
class Solution{
    struct Info{
        int l;
        int r;
        Info(int l, int r) : l(l), r(r) {
        }
    };

    /**
     * 处理以headValue节点为头的拓扑贡献记录，并更新到map中
     *
     * @param node      需要判断的节点（是v的左孩子或右孩子）
     * @param headValue BST头结点的值
     * @param map       记录表
     * @param isLChild  是否是左孩子
     * @return 总共删掉的节点个数
     */
    int modifyMap(TreeNode *node, int headValue, std::map<TreeNode *, std::shared_ptr<Info>> &map, bool isLChild){
        if(node == nullptr || !map.count(node)){
            return 0;
        }
        auto record  = map[node]; // 拿到node节点的旧记录record
        // n是左孩子且比头结点的值大，或n是右孩子且比头结点的值小，说明不满足BST，故删除
        if ((isLChild && node->val > headValue) || ((!isLChild) && node->val < headValue)) {
            map.erase(node);
            return record->l + record->r + 1; // 返回总共删掉的节点数
        } else { // n满足BST
            int minus = modifyMap(isLChild ? node->right : node->left, headValue, map, isLChild); // 如果是左子树，则递归其右边界；如果是右子树，则递归其左边界
            if (isLChild) { // 如果node本身是左子树，则其右子树的贡献记录被更新
                record->r = record->r - minus;
            } else {  // 如果node本身是右子树，则其左子树的贡献记录被更新
                record->l = record->l - minus;
            }
            // 将更新后的node的记录同步到map中
            map.insert({node, record});
            return minus;
        }
    }

    // 后序遍历左子树
    int process(TreeNode *head, std::map<TreeNode *, std::shared_ptr<Info>> &map){
        if(head == nullptr){
            return 0;
        }
        
        int ls = process(head->left, map);
        int rs = process(head->right, map);

        // 计算并处理当前节点
        modifyMap(head->left, head->val, map, true); // 生成其左孩子节点的记录
        modifyMap(head->right, head->val, map, false); // 生成其右孩子节点的记录
        auto lRecord = map[head->left];  // 拿到左孩子的记录
        auto rRecord = map[head->right]; // 拿到右孩子的记录
        int lBST = (lRecord == nullptr ? 0 : lRecord->l + lRecord->r + 1); // 计算左孩子为头的拓扑贡献记录（为生成当前节点的记录做准备）
        int rBST = (rRecord == nullptr ? 0 : rRecord->l + rRecord->r + 1); // 计算右孩子为头的拓扑贡献记录（为生成当前节点的记录做准备）
        map.insert({head, std::make_shared<Info>(lBST, rBST)}); // 生成当前节点为头的拓扑贡献记录
        return std::max(lBST + rBST + 1,  std::max(ls, rs)); // 判断以当前节点为头、以左/右孩子为头，二者哪个更大，找出所有节点的最大拓扑结构中最大的那个
    }
public:
    int bstTopoSize(TreeNode *head){
        std::map<TreeNode *, std::shared_ptr<Info>> map; // <节点，以这个节点为头的拓扑贡献记录>
        return process(head, map);
    }
};