机器学习——基于KL散度的变分推理

一、说明

        贝叶斯推理还是比较难懂的。而贝叶斯推理的作用，是将隐含的事实进行揭示，这是一个神奇并极其有用的理论。要说“透过现象看本质”的方法，最经典、最高效的方法论莫过于贝叶斯理论。本文将对此类方法进行论证。

二、贝叶斯定理

        贝叶斯定理看起来非常简单。但是，分母是在z上积分的配分函数。一般情况下，不能用解析法求解。即使我们可以使用已知的分布族对先验和似然进行建模，后验 p( z | x ) 通常仍然很棘手。

        让我们用一个简单的例子来演示一下复杂性。我们使用多项分布来选择K 个正态分布之一。然后我们用选定的正态分布对xᵢ 进行采样。如图所示，后验的复杂性已经无法管理。

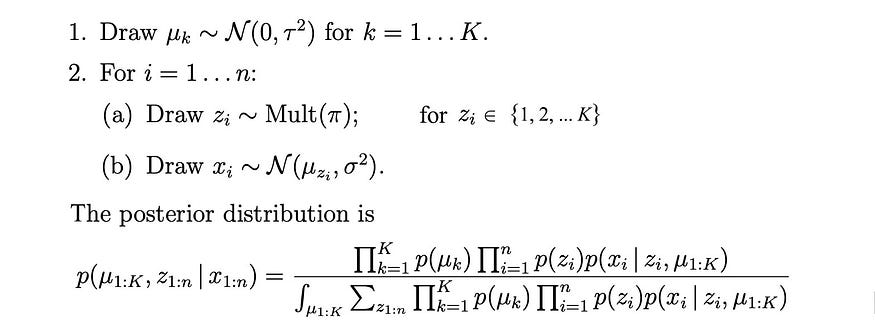
从源码修改

        另一种方法是近似解。在机器学习中，有两种主要的近似方法。它们是采样和变分推理。在本文中，我们将讨论后者。

        在变分推理中，给定观测值X，我们为潜在变量z建立概率模型q，即q ≈ p ( z|X )。

        上面的边际p ( X ) 可以计算为：

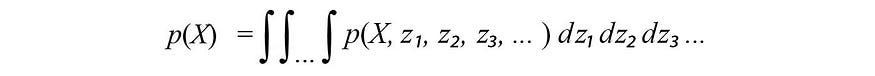
        在变分推断中，我们避免计算边际p ( X )。这个配分函数通常很难计算。相反，我们选择一些易于处理的分布q族来近似p。

        我们适合q使用样本数据来学习分布参数θ。当我们选择q时，我们确保它易于操作。例如，它的期望和归一化因子可以直接从分布参数计算。由于这种选择，我们可以使用q代替p来进行任何推断或分析。

三、LDA概述

        虽然概念听起来简单，但细节却不简单。在本节中，我们将使用著名的主题建模算法（称为潜在狄利克雷分配 (LDA)）详细阐述主要步骤。我们希望这能为您提供一个顶层概述，然后再深入研究细节和证明。

        下面是LDA的图形模型。

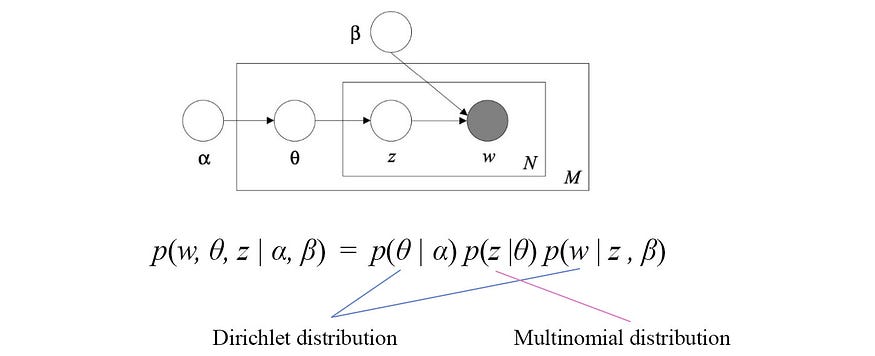
        该模型包含变量α、β、θ、z和w。不要担心变量的含义，因为它在我们的上下文中并不重要。w是我们的观察结果。θ和z是我们想要发现的隐藏变量（潜在因子）。α和β在我们的讨论中是固定且已知的。图形模型中的箭头表示依赖性。例如，w仅取决于z和β。因此，p ( w | α, β, θ, z ) 可以简化 为p (w| z, β )。

        与许多概率模型一样，我们感兴趣的是在给定已知输入的情况下对联合分布p ( w, θ, z | α, β ) 进行建模。我们应用链式法则来扩展联合概率，使其仅由单个变量的分布组成。然后，我们应用图中的依赖关系来简化每一项。我们得到

        基于主题建模问题，θ和w可以用狄利克雷分布来建模，z可以用多项分布来建模。我们的目标是对于所有隐藏变量θ和z用q近似p。

        我们定义一个目标来最小化p和q之间的差异。这可以通过最大化下面的 ELBO (证据下限) 来实现。

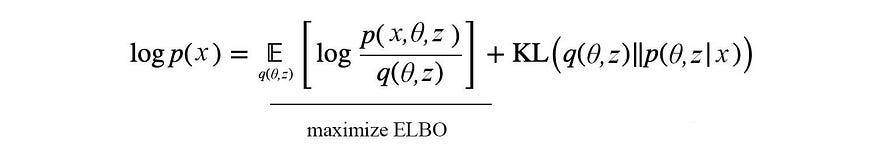
        即使不是那么明显，当p和q相同时，ELBO 最大化。然而，联合概率q ( θ, z ) 仍然很难建模。我们将其分解并近似为q ( θ, z ) ≈ q ( θ ) q ( z )。即使它可能并不完美，但实证结果通常是好的。z由多个变量z₁、z2、z₃、...组成。并且可以分解为各个分量q ( z₁ ) q ( z 2)...因此， q的最终模型为：

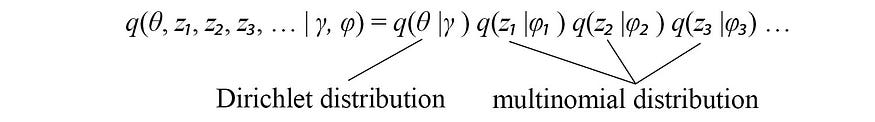
        根据主题建模问题，我们可以用狄利克雷分布对θ进行建模，用多项式分布对zᵢ进行建模，其中γ和φᵢ为相应的分布参数。 这是一个伟大的里程碑，因为我们设法用各个隐藏变量的分布来建模复杂模型，并为每个隐藏变量选择一个易于处理的分布。剩下的问题是如何学习γ和 φ ᵢ。让我们回到 ELBO 目标：

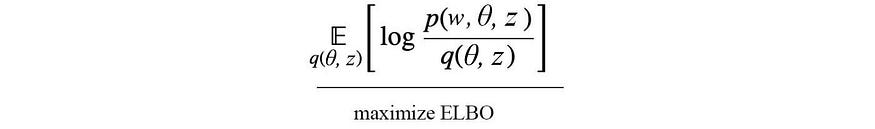
        在许多机器学习问题中，为了有效地对问题进行建模，隐藏变量通常相互依赖。我们无法一步一步地优化它们。相反，我们一次优化一个变量，同时保持其他变量固定。因此，我们以交替的步骤轮换要优化的隐藏变量，直到解收敛。在LDA中，z和θ分别在下面的步骤5和6中进行优化。

来源

        剩下的主要问题是如何在修复其他参数的同时优化变分参数。在每次迭代中，目标隐变量 z k的最优分布为：

        分子对除 z k之外的所有隐藏变量进行积分。

        听起来我们正在重新引入邪恶双胞胎：正常化因素。尽管如此，这不会成为问题。我们选择q作为易于处理的分布。它们的期望和归一化可以从分布参数中分析得出。

        方程中的分子值得更多解释。对于常规期望 E[ f ( x₁, x2, x₃ )]，我们对所有变量评估f 。

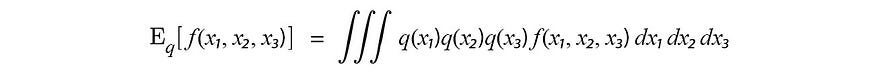
        但对于我们的分子，我们省略了目标变量。

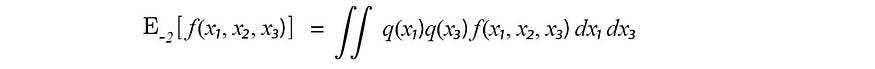
IE，

        -k是以下缩写：

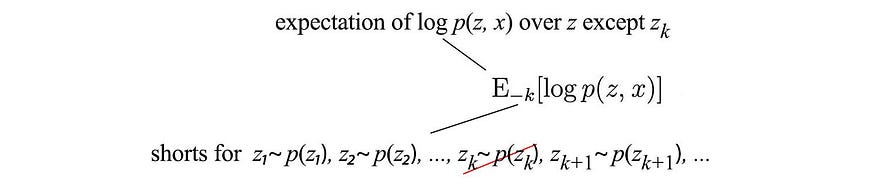
        然而，我们不会在计算期望时进行积分。我们对qᵢ的选择使我们能够简化 ELBO 最大化过程中的许多计算。让我们更详细地介绍一下。

        在 LDA 中，q近似为：

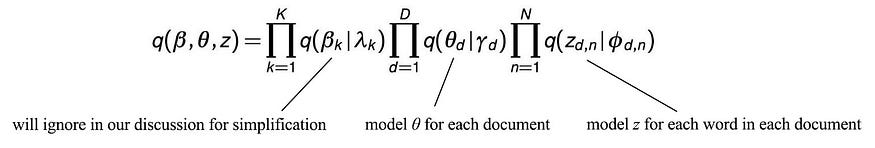
        其中θ和z分别由γ和 𝜙建模。我们的计算涉及：

1. 将 ELBO 扩展为各个变量
2. 计算期望值
3. 优化 ELBO

展开 ELBO

使用图形模型和链式法则，我们将 ELBO 展开为：

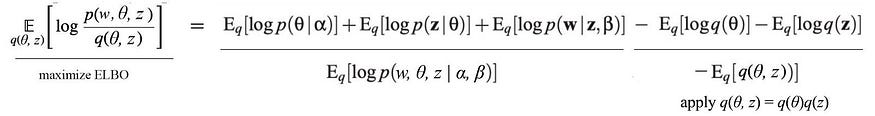
计算期望值

我们不想让您因细节而不知所措。因此，我们仅演示如何计算第一项的期望。首先，θ由参数为α 的狄利克雷分布建模。

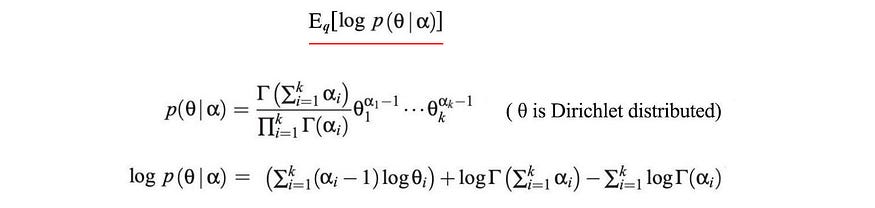
接下来，我们将计算其关于q的期望。

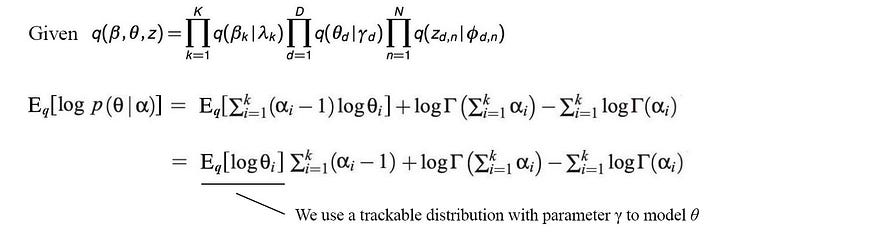
这里无需证明，E[log θᵢ ] 可以直接从 γ 计算出来。

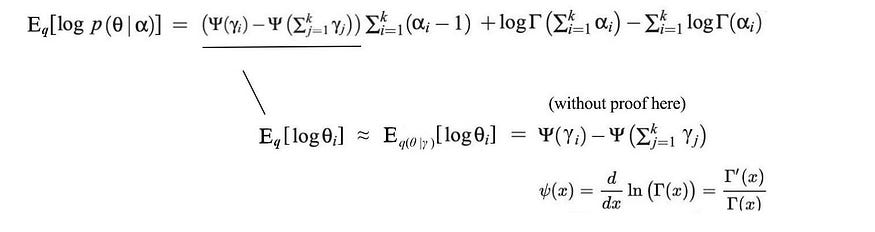
        我们深思熟虑地选择q，通常根据问题陈述中隐藏变量的属性使用众所周知的分布。数学家已经通过分析方法解决了这些期望表达式。我们甚至不用担心标准化因素。

        优化 ELBO

        在我们展开 ELBO 中的所有剩余项后，我们可以将它与γᵢ（γ中的第 i个参数）和 𝜙 nᵢ（第 n 个单词中的第 i个参数）区分开。通过将导数设置为零，我们找到γᵢ的最优解为：

        𝜙 nᵢ的最佳解决方案将是：

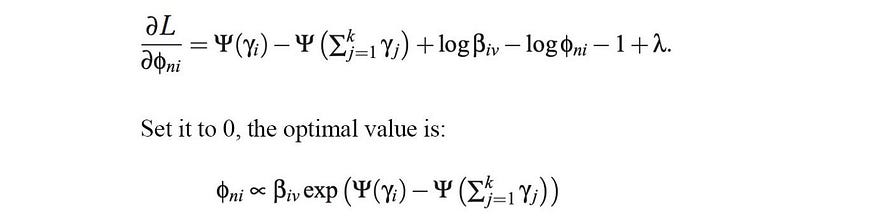
        由于γ和 𝜙 nᵢ之间的依赖性，我们将在交替步骤中迭代优化参数。

来源

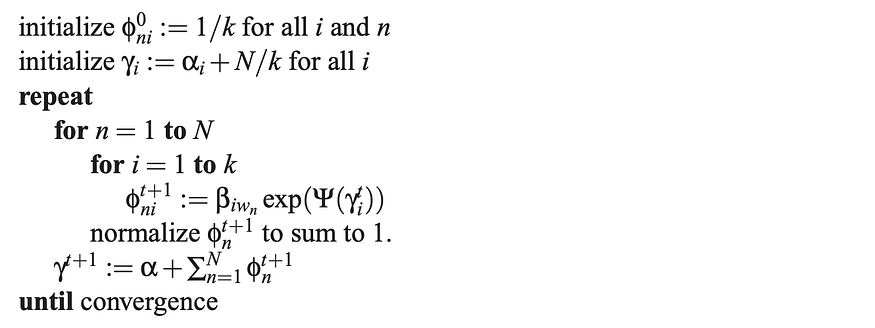
        这是概述。对于其余的文章，我们将介绍变分推理、证明和详细示例中的一些主要设计决策。

四、KL散度

        为了找到q，我们将问题转化为优化问题。我们计算q的最佳参数，以最小化目标p * 的反向 KL 散度。

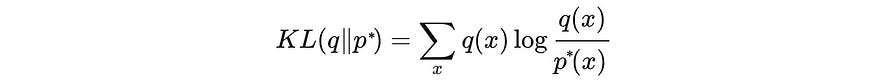
        如前所示，KL 散度不是对称的。仅当q足够复杂以对p进行建模时， q的最优解才会与KL ( p, q ) 和KL ( q,p )相同。这就提出了一个重要问题：当 KL 散度KL ( p,q )更好地匹配p的期望时，为什么要使用反向 KL 散度KL ( q, p) 。例如，当使用高斯分布对蓝色双峰分布进行建模时，反向 KL 散度解将是图 (b) 或 (c) 中的红色曲线。两种解决方案仅涵盖一种模式。

来源

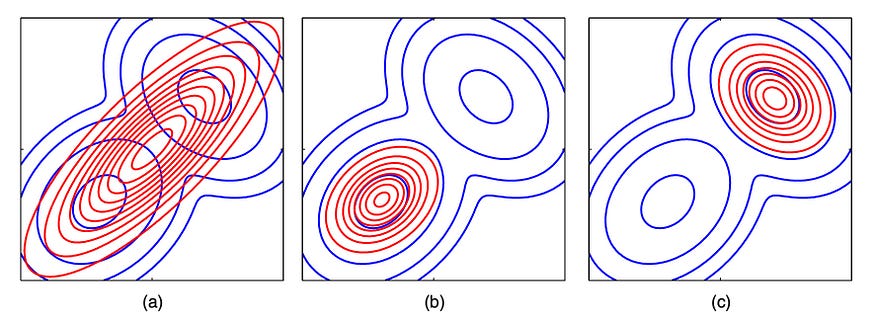
        然而，(a) 中的 KL 散度解将覆盖大部分原始分布，并且其均值将与p *的均值匹配。

        矩，包括均值和方差，描述了分布。 KL 散度解是矩投影（m 投影）。它将q与p的矩相匹配。如果我们匹配所有矩参数，它们将完全相同。如果q使用指数分布族，我们可以使用 KL 散度来精确匹配q与p *的矩。这里无需太多解释，他们预期的足够统计数据将匹配。

        （即p = q）反向 KL 散度是一种信息投影（i 投影），它不一定会产生正确的矩。由此看来，我们可以得出m投影更优越的结论。然而，如果一个机制能够精确匹配p * ，那么这样的机制也需要完全理解p * ，这首先是困难的。所以听起来并不那么好。

        在变分推理中，使用 i 投影来代替。为了证明我们的选择是合理的，让我们提出一些我们想要遵循的约束。首先，我们要避免配分函数的计算，计算很困难。其次，我们希望避免计算p ( z )，因为我们需要配分函数来计算它。因此，让我们为p定义一个新术语，即非正态分布，它将配分函数分开。

        让我们将新定义代入反向 KL 散度中。

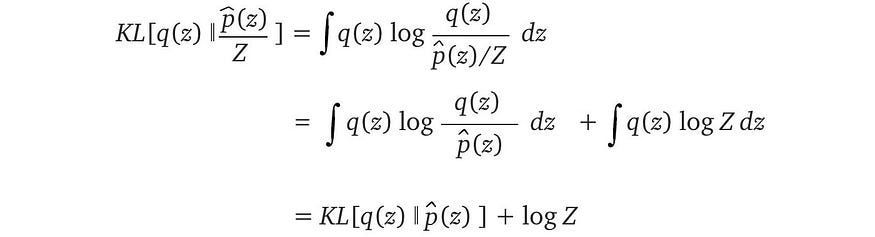
        Z不随q变化。当我们最小化反向 KL 散度时，可以忽略它。

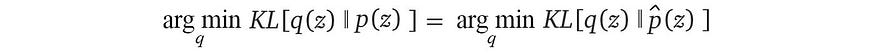
        这是个好消息。在图形模型中，未归一化的p使用因子定义明确。它们易于计算，并且 RHS 中的目标不需要任何归一化。使用反向 KL 散度是一个很好的折衷方案，即使在某些情况下它可能并不完美。由于q与p*相比过于简单， 结果可能会很糟糕。然而，变异推断通常会显示出良好的经验结果。接下来，让我们看看如何优化反向 KL 散度。

五、证据下限 (ELBO)

        让我们介绍一下下面关于凸函数f和称为证据下界 (ELBO)的 Jensen 不等式

        该图源自维基百科

        在最后一步中将 Jensen 不等式应用于凹函数后，ELBO 实际上是证据的下界 (log p ( x ))。

从源码修改

        ELBO 与 KL 散度的关系为：

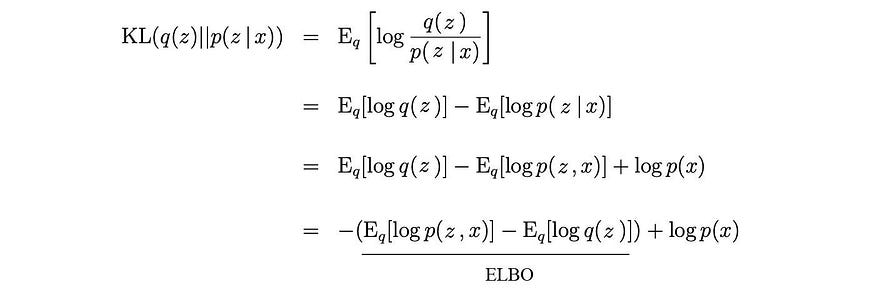
从源码修改

        现在让Z为边际p ( x )。不要将Z与隐藏变量z混淆。不幸的是，我们需要用大写字母来重载符号，因为Z经常在其他文献中使用。

        Z不会因我们对q建模的方式而改变。所以从优化q的角度来看，log Z是一个常数。

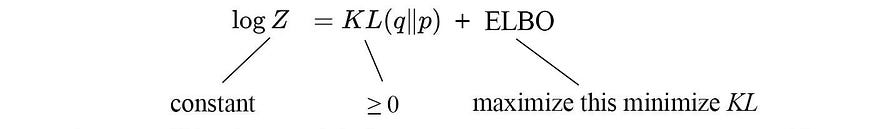
        因此，最小化 KL 散度与最大化 ELBO 相同。直观上，给定任何分布q ，ELBO 始终是 log Z的下界。然而，当q等于p*时，差距减小到零。因此，最大化 ELBO 将 KL 散度降低至零。

通过最大化证据下限 ELBO，我们可以最小化两个数据分布的差异。

        让我们将 ELBO 概括为

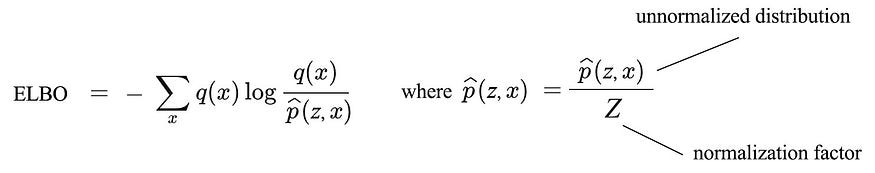
        其中Z现在是一般归一化因子。

        同样，如上所示，最大化 ELBO 与最小化 KL 散度相同，因为Z不随我们建模q 的方式而变化。

        这比 KL 散度具有重大优势。 ELBO 对于标准化和非标准化分布都适用，并且无需计算常规 KL 散度定义所需的Z。

ELBO 和图形模型（可选）

让我们演示如何使用图形模型在 ELBO 中计算非标准化分布。联合概率分布可以通过马尔可夫随机场建模为：

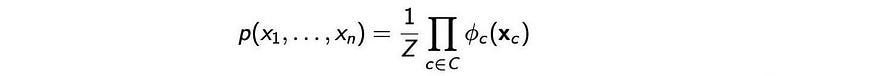
我们用上面的因子 𝜙替换 ELBO 中的非标准化p 。

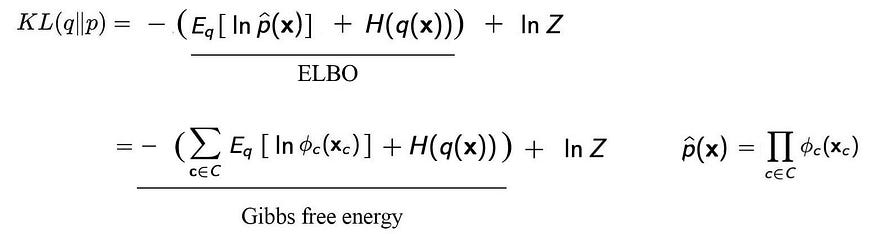
        因此，最小化 KL 散度相当于最小化吉布斯自由能。我们称之为自由能，因为它是我们可以通过改变构型来操纵的能量的一部分。如果我们使用能量模型来扩展该模型，则可以进一步扩展该模型。

六、平均场变分推理

（来源：证明和方程源自此处。）

        别高兴得太早。我们错过了变分推理中一个重要而困难的步骤。q 的选择是什么？当q包含多个变量时，即q ( z ) = q ( z₁, z₂, z₃, … )，这会变得极其困难。为了进一步降低复杂性，均值场变分推理做出了一个大胆的假设，即分布可以分解为每个仅涉及一个隐藏变量的分布。

        然后，我们根据问题使用易于处理的分布对每个分布进行建模。我们选择的分布将很容易进行分析。例如，如果z₁是多项式，我们用多项式分布对其进行建模。如前所述，许多隐藏变量相互依赖。所以我们将使用坐标下降来优化它。我们将隐藏变量分组，每个组包含自变量。我们交替旋转和优化每组变量，直到解收敛。

        所以最后一个难题是如何在每个迭代步骤中优化qᵢ ( zᵢ )。我们先介绍几个概念。当x不依赖于z时，概率的链式法则可以写成如下：

        其次，由于我们将q ( z ) 建模为独立分量qᵢ ( zᵢ )，因此我们可以将熵建模为个体熵的总和。

        有了这些信息，我们扩展了 ELBO

        进入

        zⱼ在z中的顺序是非常任意的。在下面的等式中，我们将 z k设为最后一个元素。并将与z无关的所有内容分组为常数。因此，方程变为

        我们进一步去掉与zk无关的项，然后用积分形式表示。

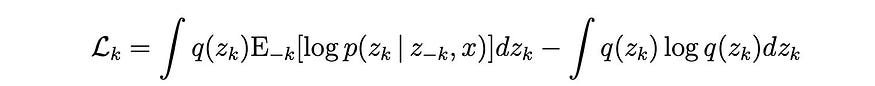
        我们取导数并将其设置为零以找到优化分布q ( zk )。

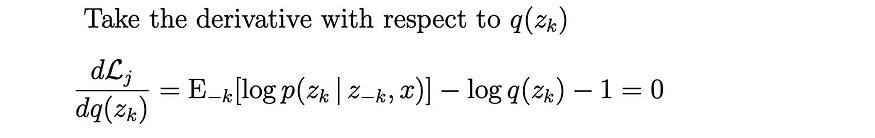
        最优解是

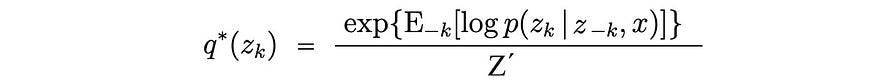
        所有常数被吸收并转化为 Z'。我们可以用贝叶斯定理来展开分子。同样，相应的分母将与zk无关，因此被吸收为归一化因子。

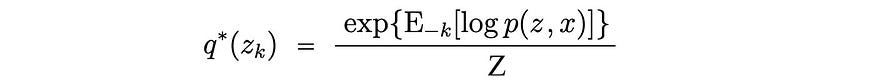
        这与我们在概述部分得到的方程相同。

        还有其他方法可以找到优化的q。让我们将所有内容放在 MRF 的上下文中。如前所述，我们的目标是

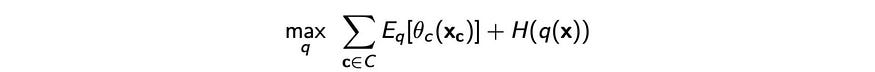
        让我们用q ( x ) 将其展开为q ( x₁ ) q ( x2 ) q ( x₃ ) …

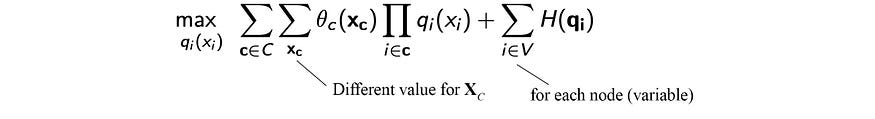
        这个方程可以用类似于MAP推论的线性代数来求解。但我们不会在这里详细介绍解决方案。

七、回顾

        我们知道分布p的方程。但分析或操纵它是令人讨厌的。

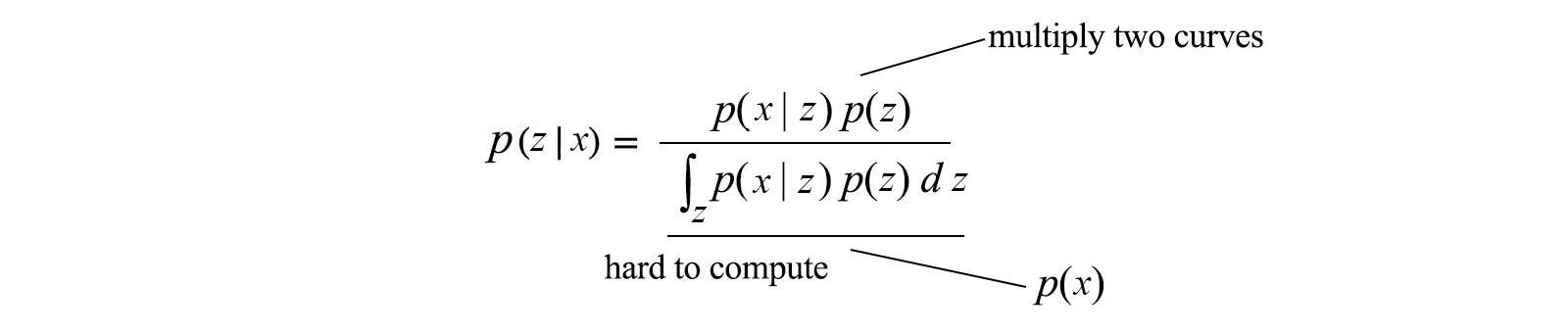
        因此，根据观察结果，我们将为每个单独的模型参数使用易于处理的qᵢ来建模p 。例如，

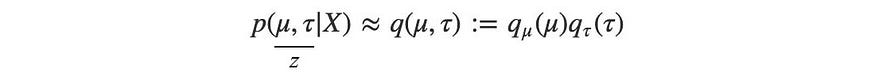
        为了最小化p和q之间的差异，我们最大化下面的 ELBO。

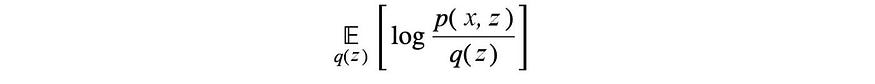
        在每个迭代步骤中，相应模型参数zⱼ的最优解为：

        由于每个q都被选为易于处理的，因此可以通过分析并且相当直接的方式找到期望值或归一化因子（如果需要）。

八、例子

（信用：示例和一些方程源自此处。）

让我们用一个例子来演示一下变异推理。考虑下面的分布p ( x )：

其中μ（平均值）和τ（精度）分别通过高斯分布和伽玛分布建模。因此，让我们用q ( μ, τ ) 来近似p ( x , μ , τ ) 。通过方差推断，我们可以从数据中学习这两个参数。每次迭代中μ和τ 的最优值将满足

因此，我们首先用链式法则展开 p ( x , μ, τ ) ，然后根据问题定义定义p来评估p ( x , μ, τ ) 。

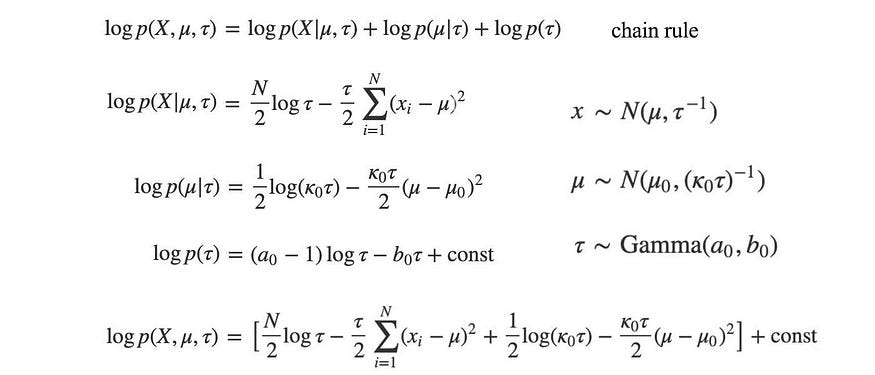
我们的下一个任务是使用下面的平均场变分推理通过q来近似p 。

现在，应用平均场变化推断，我们得到：

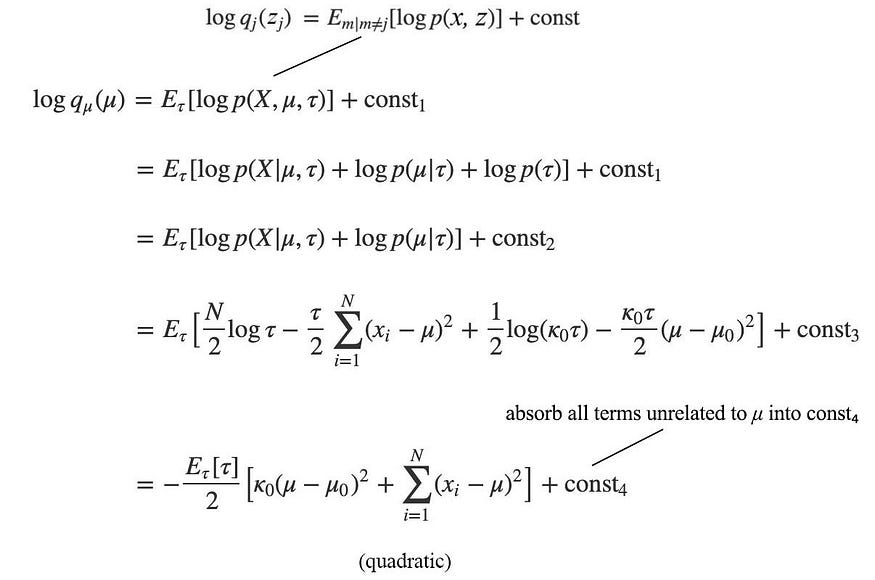
log q是二次的。所以q是高斯分布的。

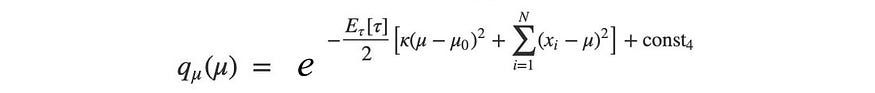
我们的下一个任务是将上面的方程与高斯定义相匹配，以找到参数μ和τ ( τ ⁻¹ = σ ²)。

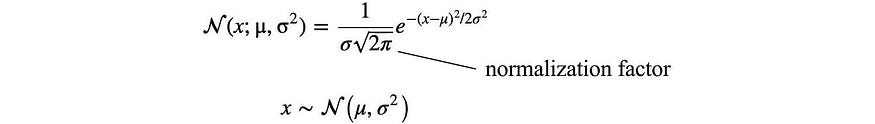
因此，μ和τ为：

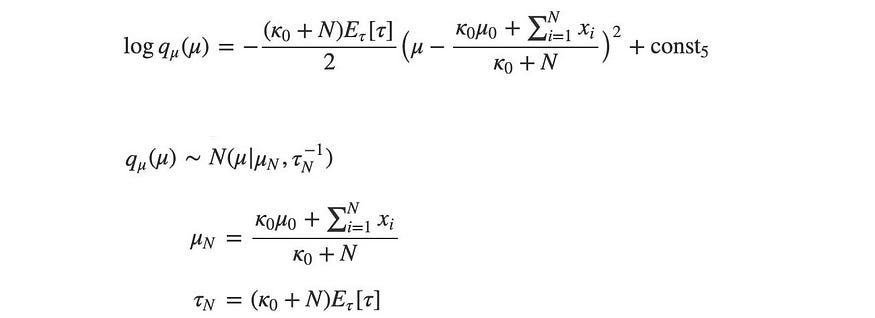
如前所述，计算归一化Z通常很困难，但对于这些众所周知的分布来说却并非如此。如果需要，可以通过分布参数计算归一化因子。我们需要集中精力寻找这些参数。

我们在计算 log q ( τ )时重复相同的过程。

τ是 Gamma 分布，因为上面的分布仅取决于τ和log τ。Gamma 分布对应的参数a和b为：

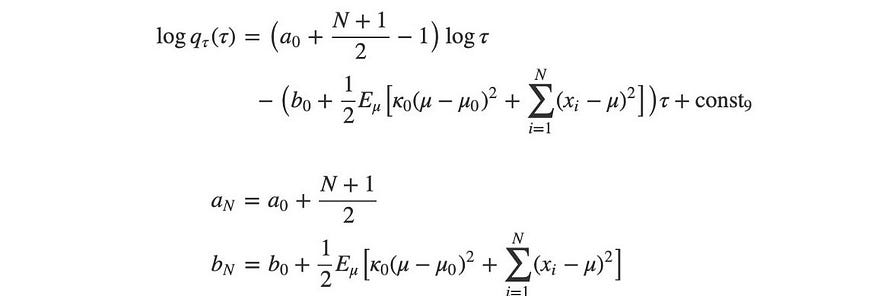
现在，我们有两个易于处理的分布，我们想要找到它们的参数μ和τ。

再次，让我们将一些术语重写为期望形式。

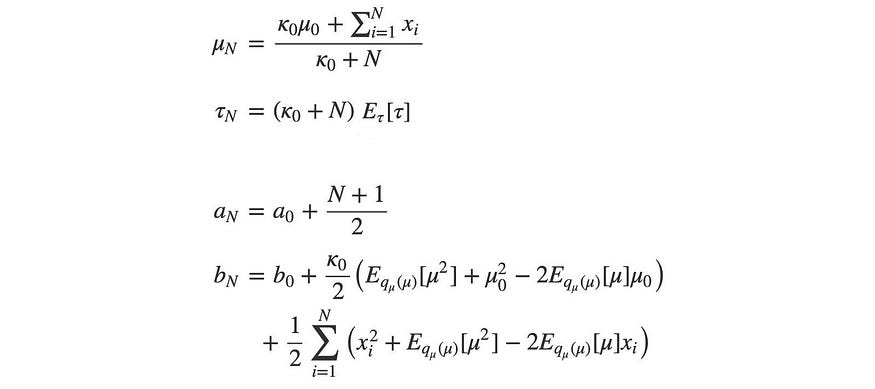
正如之前所承诺的，数学已经解析地解决了这些期望项。我们甚至懒得计算任何标准化因子。

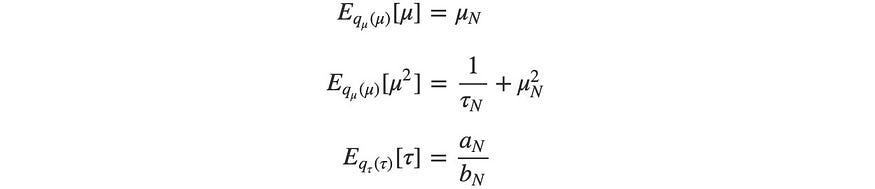
μ和a可以立即求解。但τ取决于b，而b取决于τ。

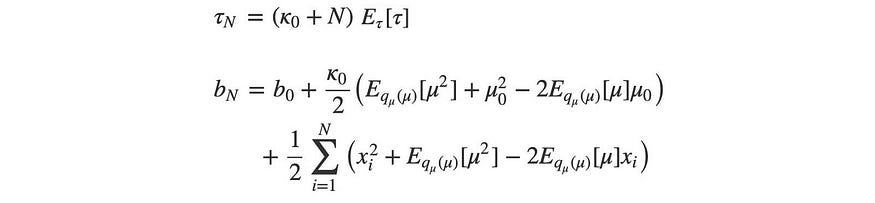
因此，我们将通过交替步骤迭代地解决它们。

1. 将 τ n初始化为某个任意值。
2. 用上面的方程求解 b n 。
3. 用上面的方程求解 τ n 。
4. 重复最后两个步骤，直到值收敛。

九、采样与变分推理

        采样方法有一个主要缺点。我们不知道当前的采样解决方案与基本事实相差多远。我们希望如果我们进行足够的采样，解决方案就会接近，但没有定量测量。为了测量这种距离，我们需要一个目标函数。由于变分推理被表述为优化问题，我们确实对进展有一定的指示。然而，变分推理近似解而不是找到精确解。事实上，我们的解决方案不太可能是精确的。

更多读物

https://jonathan-hui.medium.com/machine-learning-variational-inference-273d8e6480bb