组合数取模就是求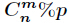

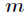
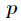
下面学习三种求法,参考ACdreamer大神
1、当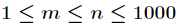
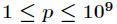

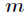
代码:
void getc(){
memset(C, 0, sizeof(C));
C[0][0] = 1;
for(int i = 1; i < maxn; i++){
C[i][0] = 1;
for(int j = 1; j < maxn; j++)
C[i][j] = (C[i-1][j-1] + C[i-1][j]) % mod;
}
}2、
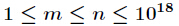 和
和
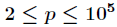 ,并且
,并且
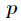 是素数
是素数
采用Lucas定理
补充两个结论:
结论1. Lucas(n,m,p)=c(n%p,m%p)*Lucas(n/p,m/p,p);
结论2. 把n写成p进制a[n]a[n-1]a[n-2]...a[0],把m写成p进制b[n]b[n-1]b[n-2]...b[0],则C(n,m)与C(a[n],b[n])*C(a[n-1],b[n-1])*C(a[n-2],b[-2])*....*C(a[0],b[0])模p同余。
所以如果
那么得到
这样然后分别求,采用逆元计算即可。
求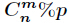 ,其中
,其中
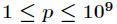 ,并且
,并且
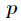 是素数的代码:
是素数的代码:
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef long long LL;
LL n,m,p;
LL quick_mod(LL a, LL b)
{
LL ans = 1;
a %= p;
while(b)
{
if(b & 1)
{
ans = ans * a % p;
b--;
}
b >>= 1;
a = a * a % p;
}
return ans;
}
LL C(LL n, LL m)
{
if(m > n) return 0;
LL ans = 1;
for(int i=1; i<=m; i++)
{
LL a = (n + i - m) % p;
LL b = i % p;
ans = ans * (a * quick_mod(b, p-2) % p) % p;
}
return ans;
}
LL Lucas(LL n, LL m)
{
if(m == 0) return 1;
return C(n % p, m % p) * Lucas(n / p, m / p) % p;
}
int main()
{
int T;
scanf("%d", &T);
while(T--)
{
scanf("%I64d%I64d%I64d", &n, &m, &p);
printf("%I64d\n", Lucas(n,m));
}
return 0;
} 如果p比较小,可以打表处理n!(将上面的C()函数换成下面两个)
void init(){
fac[0]=1;
for(int i=1;i<=maxn;i++)
fac[i]=fac[i-1]*i%mod;
}
ll C(ll n,ll m){
if(n<m)return 0;
return fac[n]*quickmod(fac[m]*fac[n-m],mod-2);
} 和
和
 ,并且
,并且
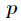 可能为合数
可能为合数
对n和m分解质因数,然后用快速幂乘起来。
我们要求的是n!/(m! *(n-m)!),n!肯定可以整除(m! *(n-m)!),所以后面两个有的因子,n!都有,只要将它们因子的指数相加减,然后快速幂相乘取模即可。
代码:
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
typedef long long LL;
const int N = 200005;
bool prime[N];
int p[N];
int cnt;
void isprime()
{
cnt = 0;
memset(prime,true,sizeof(prime));
for(int i=2; i<N; i++)
{
if(prime[i])
{
p[cnt++] = i;
for(int j=i+i; j<N; j+=i)
prime[j] = false;
}
}
}
LL quick_mod(LL a,LL b,LL m)
{
LL ans = 1;
a %= m;
while(b)
{
if(b & 1)
{
ans = ans * a % m;
b--;
}
b >>= 1;
a = a * a % m;
}
return ans;
}
LL Work(LL n,LL p)
{
LL ans = 0;
while(n)
{
ans += n / p;
n /= p;
}
return ans;
}
LL Solve(LL n,LL m,LL P)
{
LL ans = 1;
for(int i=0; i<cnt && p[i]<=n; i++)
{
LL x = Work(n, p[i]);
LL y = Work(n - m, p[i]);
LL z = Work(m, p[i]);
x -= (y + z);
ans *= quick_mod(p[i],x,P);
ans %= P;
}
return ans;
}
int main()
{
int T;
isprime();
cin>>T;
while(T--)
{
LL n,m,P;
cin>>n>>m>>P;
cout<<Solve(n,m,P)<<endl;
}
return 0;
} 假设n=200,那么因子5的个数=200/5+40/5+8/5=49,怎么得到的呢?200中5的倍数有40个,这40个数中其中是25的倍数的有8个,所以还能分解出8个5,这8个数中还有一个是125的倍数,还能分解出一个5,就这样一直循环下去,就能求出指数的值。
(起初一直没明白work这个函数,看了http://blog.csdn.net/knight_kaka/article/details/24874743这篇文章后豁然开朗,感谢)
另外还有 n,m≤10^9,p≤10^5可能是合数,与第3种相比n和m比较大,这种情况暂且不写了,可以参考http://blog.csdn.net/aarongzk/article/details/50654358这篇文章。
例题以后再补上。










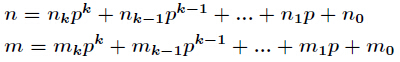














 2836
2836

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








