给出两个字符串A B,求A与B的最长公共子序列(子序列不要求是连续的)。
输出示例
比如两个串为:
abcicba
abdkscab
ab是两个串的子序列,abc也是,abca也是,其中abca是这两个字符串最长的子序列。
输入
第1行:字符串A 第2行:字符串B (A,B的长度 <= 1000)
输出
输出最长的子序列,如果有多个,随意输出1个。
输入示例
abcicba abdkscab
输出示例
abca
求解:
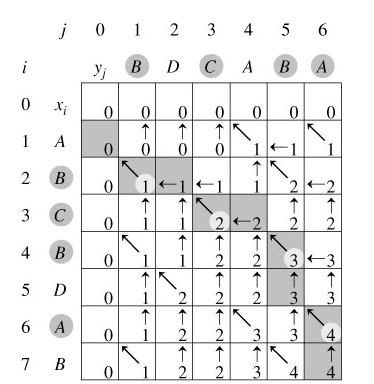
引进一个二维数组c[][],用c[i][j]记录X[i]与Y[j] 的LCS 的长度,b[i][j]记录c[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向。 我们是自底向上进行递推计算,那么在计算c[i,j]之前,c[i-1][j-1],c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j],就可以计算出c[i][j]。
问题的递归式写成:
回溯输出最长公共子序列过程:
算法分析: 由于每次调用至少向上或向左(或向上向左同时)移动一步,故最多调用(m + n)次就会遇到i = 0或j = 0的情况,此时开始返回。返回时与递归调用时方向相反,步数相同,故算法时间复杂度为o(m + n)。
#include<iostream>
#include<iomanip>
#include <string.h>
using namespace std;
long int c[1001][1001];
int main()
{
string a,b;
char d[1000];
long long int n1,n2,i,j,k;
cin>>a>>b;
//n1=strlen(a);strlen(用于数组中)
//n2=strlen(b);
n1=a.size();
n2=b.size();
k=0;
for(i=1;i<=1000;i++){c[0][i]=0;c[i][0]=0;}
for(i=1;i<=n1;i++)
for(j=1;j<=n2;j++)
c[i][j]=(a[i-1]==b[j-1])?(c[i-1][j-1]+1):max(c[i][j-1],c[i-1][j]);
for(i=n1,j=n2;i>=1&&j>=1;)
{
if(a[i-1]==b[j-1])
{
d[k]=a[i-1];
k++;
i--;
j--;
}
else
{
if(c[i][j-1]>c[i-1][j])//也可以等于,无所谓,等于的话回溯路线会有所改变
{
j--;
}
else
{
i--;
}
}
}
for(i=k-1;i>=0;i--)cout<<d[i];
cout<<endl;
return 0;
}







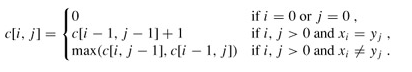














 3386
3386

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








