查找算法之二分查找算法
1. 概述
二分查找算法也称折半查找算法,是在有序数组中用到的较为频繁的一种查找算法。在未接触二分查找算法时,最通用的一种做法是,对数组进行遍历,跟每个元素进行比较,即顺序查找。二分查找较顺序查找更优,因为这种算法每一次比较都使查找范围缩小一半。
2. 算法思想
二分查找算法是建立在有序数组基础上的。算法思想为:
- 查找过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则查找过程结束;
- 如果某一待查找元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟第1点一样从中间元素开始继续进行查找。
- 如果在某一步骤数组为空,则代表找不到。
算法实现思路:
- 找出位于数组中间的值(为便于表述,将该值放在一个临时变量tmp中)。
- 需要找到的key和tmp进行比较。
- 如果key值大于tmp,则把数组中间位置作为下一次计算的起点;重复第1、2步骤继续查找。
- 如果key值小于tmp,则把数组中间位置作为下一次计算的终点;重复第1、2步骤继续查找。
- 如果key值等于tmp,则返回数组下标,完成查找。
3. 算法实现
package com.demo;
/**
* 二分查找算法
*
* @author 小明
*
*/
public class BinarySearch {
/**
* 二分查找:非递归方式查找
*
* @param array
* 排序数组
* @param key
* 待查找元素
* @return 查找到元素在数组中的索引,-1表示未找到
*/
public static int search(int[] array, int key) {
// 头指针、尾指针、中间指针
int head = 0, tail = array.length - 1, middle;
while (head <= tail) { // 头指针在尾指针之前
middle = (head + tail) >> 1; // 通过头、尾指针位置求中间位置
if (key > array[middle]) { // 待查找元素在中间指针元素后
head = middle + 1;
} else if (key < array[middle]) { // 待查找元素在中间指针元素之前
tail = middle - 1;
} else { // 待查找元素与中间指针元素相等
return middle;
}
}
return -1; // 返回-1表示未找到
}
/**
* 入口方法,测试
* @param args
*/
public static void main(String[] args) {
int[] array = {3, 7, 9, 12, 87, 99, 126};
int key = 87;
int index = search(array, key);
if (index != -1){
System.out.println("查找到在数组中的索引:" + index);
} else {
System.out.println("未查找到该元素");
}
}
}上述示例是使用非递归的方式实现二分查找,当然也可以使用递归的方式来实现:
/**
* 二分查找:递归实现
*
* @param array
* 排序数组
* @param key
* 待查找元素
* @param head
* 头指针索引
* @param tail
* 尾指针索引
* @return 查找到元素在数组中的索引,-1表示未找到
*/
public static int search(int[] array, int key, int head, int tail) {
if (head > tail) { // 头指针在尾指针之后,说明找不到元素
return -1;
}
int middle = (head + tail) >> 1; // 通过头、尾指针索引求中间位置索引
if (key > array[middle]) { // 待查找元素在中间指针元素后
return search(array, key, middle + 1, tail);
} else if (key < array[middle]) { // 待查找元素在中间元素之前
return search(array, key, head, middle - 1);
} else { // 待查找元素与中间指针元素相等
return middle;
}
}







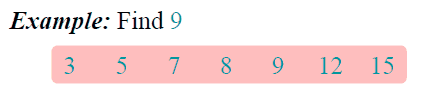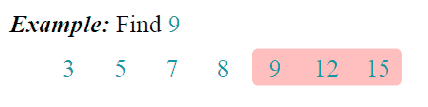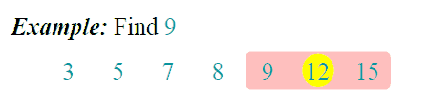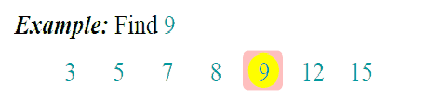














 1683
1683

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








