转载请声明出处:http://blog.csdn.net/zhongkelee/article/details/44490315
说在前面
这学期正在学习《计算机算法设计与分析》,所以用博客的形式记录自己的学习心得,与大家交流分享。
一、算法渐进复杂性及其相关记号
1. 复杂度概念
算法的复杂性分析,说白了也就是关于计算机程序的性能和算法所用计算机资源的理论分析。通常包括时间复杂性T(n)和空间复杂性S(n),其中n是问题的输入规模。一般来说算法需要的时间与输入的规模同步增长,所以通常把一个程序的运行时间描述成输入规模的函数。
对许多问题,比如排序或计算离散傅里叶变换最自然的量度是输入中的项数,例如带排序数组的规模n。对许多其他问题,比如两个整数相乘,输入规模的最佳量度是用通常的二进制记号表示输入所需的总位数。
通常一个算法的运行时间依赖于输入,而我们想要获取的是运行时间的上界(实际上每个人都更倾向于获得一种保证)。
最坏情况下的时间复杂性:
最好情况下的时间复杂性:
平均情况下的时间复杂性:
其中 I 是问题的规模为 n 的实例,p(I) 是实例I出现的概率。
2. 渐近复杂性
如果我们忽略机器相关的参数,只考察 T(n) 随着 n 趋于无穷大的增长,则可以引入渐近复杂性的概念:
t(n) 是 T(n) 的渐进性态,是 T(n) 略去低阶项后留下的主项,我们称作算法的渐进复杂性。
例如,当 n 足够大时,一个的算法总是能够打败一个
的算法。
在后文中,我们使用如下渐进分析记号:
其实,这5个记号可以理解为:
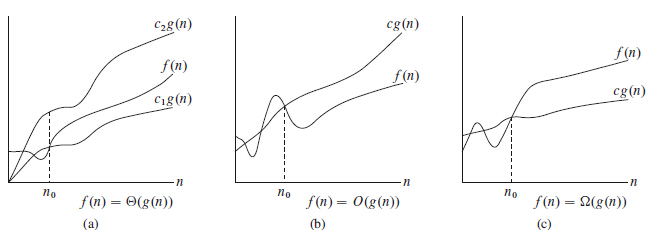
若对所有的,函数f(n)在一个常量因子内等于g(n),就称g(n)是f(n)的一个渐进紧确界,如下图所示:
有关算法分析中渐进函数、常用函数的若干条性质,我这里就不再赘述了,可以参考《算法导论》第三版29~34页相关内容及证明。
3. 最优算法
如果问题的计算时间下界为,则计算时间复杂性为
的算法,就可以称为最优算法。例如,比较排序问题的计算时间下界为
,计算时间复杂性为
的排序算法是最优算法(比如堆排序算法,后续博客会详细讲解该算法)。
4.常见时间复杂度
常见时间复杂度从低到高为:常数 < 对数< 多项式 < 指数 < 阶乘。
二、普通算法复杂度分析
1. 顺序搜索算法
例如,顺序搜索算法:
Template<class Type>
Int seqSearch(Type *a, int n, Type k){
for(int i = 0; i < n; i++)
if(a[i] == k)
return i;
return -1;
}它的三种时间复杂性计算如下:








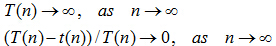

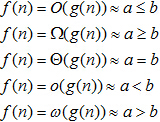
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








