超级会员免费看
这篇博客通过R语言进行了单因素方差分析（One-Way ANOVA）实战，包括数据仿真、探索性数据分析（EDA）、模型解读、方差齐性检验和TukeyHSD差异分析。结果表明不同锻炼方案对体重减轻的平均影响有统计学显著差异。
R语言单因素方差分析（One-Way ANOVA）实战：探索性数据分析（EDA）、单因素方差分析模型结果解读（检查模型假设）、分析不同分组的差异TukeyHSD、单因素方差分析的结果总结
目录
R语言单因素方差分析（One-Way ANOVA）实战：探索性数据分析（EDA）、单因素方差分析模型结果解读（检查模型假设）、分析不同分组的差异TukeyHSD、单因素方差分析的结果总结
#探索性数据分析（使用dplyr包计算不同分组的方差和均值）
#单因素方差分析（One-Way ANOVA）
单因素方差分析（One-Way ANOVA）分析一个预测变量如何影响一个反应变量。相反，如果我们对两个预测变量如何影响一个响应变量，我们可以进行双向方差分析（Two-Way ANOVA）。
单因素方差分析（“方差分析”）用于确定单个因子的多个独立组的均值之间是否有统计学意义上的差异（均值的差异）。
#仿真数据
假设我们想确定三种不同的运动方案是否对减肥有不同的影响。我们正在研究的预测变量是锻炼计划，响应变量（response variable）是体重减轻，以磅为单位。我们可以进行一个单因素方差分析，以确定三个方案的结果体重减轻之间是否有统计学意义上的差异。
我们招募了90人参加一个实验，在这个实验中，我们随机分配30人跟随方案A,方案B或方案C一个月，以确定三个方案的结果体重减轻之间是否有统计学意义上的差异。
dataframe的第一列显示了该人参加了一个月的项目（A、B、C），第二列显示了该人在项目结束时经历的总体重减轻，以磅为单位。
#make this example reproducible
set.seed(0)
#create data frame
data <- data.frame(program = rep(c("A", "B", "C"), each = 30),
weight_loss = c(runif(30, 0, 3),
runif(30, 0, 5),
runif(30, 1, 7)))
#view first six rows of data frame
head(data)
# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458#探索性数据分析（使用dplyr包计算不同分组的方差和均值）
在我们拟合单因素方差分析模型之前，我们可以通过使用dplyr包找到三个方案中每一个方案的体重减轻的均值和标准差来更好地理解我们的数据。
#load dplyr package
library(dplyr)
#find mean and standard deviation of weight loss for each treatment group
data %>%
group_by(program) %>%
summarise(mean = mean(weight_loss),
sd = sd(weight_loss))
# A tibble: 3 x 3
# program mean sd
#
#1 A 1.58 0.905
#2 B 2.56 1.24
#3 C 4.13 1.57 #探索性数据分析（箱图boxplot可视化）
#create boxplots
boxplot(weight_loss ~ program,
data = data,
main = "Weight Loss Distribution by Program",
xlab = "Program",
ylab = "Weight Loss",
col = "steelblue",
border = "black")
从箱图中我们可以看到，方案C的参与者的平均体重减轻量最高，方案A的参与者的平均体重减轻量最低，即减肥效果差。
我们还可以看到，方案C的体重减轻标准差（方块图的“长度”）比其他两个方案大得多。
接下来，我们将对我们的数据进行单因素方差分析，看看这些视觉差异是否真的有统计学意义。
#拟合单因素方差分析模型
拟合R中的单因素方差分析模型的一般语法如下：
aov(response variable ~ predictor_variable, data = dataset)
在我们的示例中，我们可以使用下面的代码来拟合单因素方差分析模型，使用weight_loss作为响应变量（response），使用program作为预测变量（predictor）。
然后，我们可以使用summary（）函数查看模型的输出。
#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)
#view the model output
summary(model)
# Df Sum Sq Mean Sq F value Pr(>F)
#program 2 98.93 49.46 30.83 7.55e-11 ***
#Residuals 87 139.57 1.60
#---
#Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1从模型输出可以看出，预测变量锻炼方案（A、B、C）的p值接近0 ，小于显著性水平0.05，那么拒绝原假设（原假设为没有差异），选择备则假设。
换句话说，三个项目的平均体重减轻有统计学上的显著差异。
#单因素方差分析模型结果解读（检查模型假设）
#我们需要提前确认模型的假设前提是否满足，如果假设前提不满足我们分析p值或者查看统计量拒绝或者接受原假设都没有任何意义。
在我们进一步研究之前，我们应该检查我们模型的假设是否满足，以便我们从模型中得到的结果是可靠的。特别是，单因素方差分析的假设前提：
1.独立性（Independence）：各组的观察（样本）必须相互独立。由于我们采用了随机设计（即我们随机分配参与者参加锻炼项目A、B、C），这个假设应该是符合的，所以我们不需要太担心这一点。
2.正态性（Normality）：因变量对预测变量（predictor，此处就是锻炼方式）的每一个级别都应近似正态分布。
3.方差相等（Equal Variance）：每组的方差相等或近似相等。
检验正态性和方差相等假设的一种方法是使用函数plot()，它产生四个模型检验图。我们尤其对以下两个图像最感兴趣：
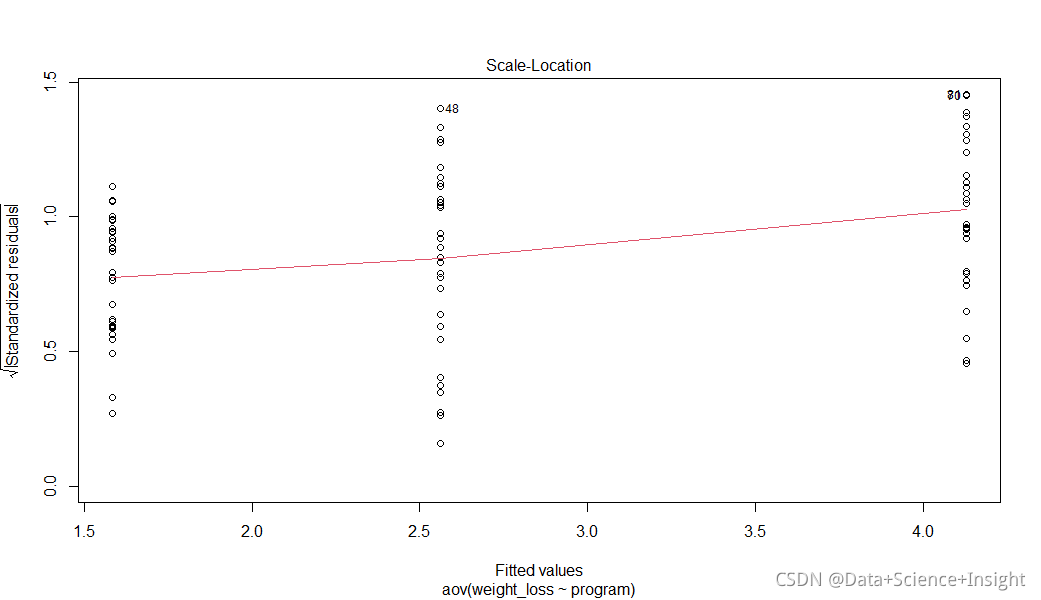
残差与拟合值（Residuals vs Fitted）：此图显示了残差与拟合值之间的关系。我们可以用这个图来粗略地衡量各组之间的方差是否近似相等。
Q-Q图（Q-Q Plot）：此图显示了与理论分位数相对应的标准化残差。我们可以用这个图来粗略地衡量是否满足正态性假设。
#plot函数打印模型进行可视化
plot(model)
残差与拟合图允许我们检查我们的等方差假设。理想情况下，我们希望看到残差在拟合值的每一个级别上均匀分布。我们可以看到，对于较高的拟合值，残差要分散得多，这表明我们的等方差假设可能被违反。
Q-Q图允许我们检查正态性假设。理想情况下，标准化残差将沿图中的直对角线下降。然而，在上面的图形中，我们可以看到残差在开始和结束时偏离了标准对角线。这表明我们的正态性假设可能被违反。
#使用car包的Levene's检验检验等方差性
#load car package
library(car)
#conduct Levene's Test for equality of variances
leveneTest(weight_loss ~ program, data = data)
#Levene's Test for Homogeneity of Variance (center = median)
# Df F value Pr(>F)
#group 2 4.1716 0.01862 *
# 87
#---
#Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1检验的p值为0.01862。如果我们使用0.05的显著性水平，我们将拒绝三个程序的方差相等的无效假设(零假设、原假设)。然而，如果我们使用0.01的显著性水平，我们不会拒绝无效假设。
虽然我们可以尝试转换数据以确保满足我们的正态性和方差相等的假设，但目前我们不会太担心这一点。
#分析不同锻炼方法的差异TukeyHSD
一旦我们证实模型假设满足（或合理满足、近似满足），我们就可以进行后事后分析和测试（post hoc），以确定治疗组彼此之间的确切差异。
对于我们的事后测试，我们将使用函数TukeyHSD来执行tukey的多个比较测试。
#perform Tukey's Test for multiple comparisons
TukeyHSD(model, conf.level=.95)
# Tukey multiple comparisons of means
# 95% family-wise confidence level
#
#Fit: aov(formula = weight_loss ~ program, data = data)
#
#$program
# diff lwr upr p adj
#B-A 0.9777414 0.1979466 1.757536 0.0100545
#C-A 2.5454024 1.7656076 3.325197 0.0000000
#C-B 1.5676610 0.7878662 2.347456 0.0000199p值表示每个锻炼方法（A、B、C）之间是否有统计学意义上的差异。我们可以从输出中看到，在0.05显著性水平上，每个程序的平均体重减轻有统计学显著性差异。
我们还可以通过使用R中的plot（TukeyHSD（））函数来可视化从Tukey测试中得到的95%置信区间。
#create confidence interval for each comparison
plot(TukeyHSD(model, conf.level=.95), las = 2)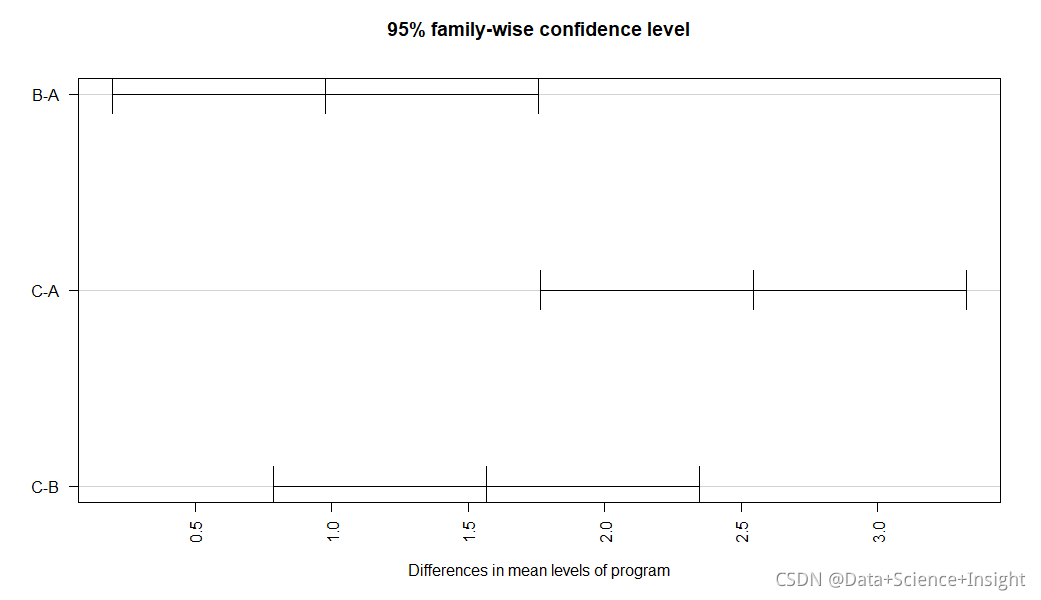
置信区间的结果与假设检验的结果是一致的。
特别地，我们可以看到不同锻炼方法间平均体重降低的置信区间中没有一个包含零值，这表明所有三个程序之间的平均体重损失存在统计上的显著差异。
这与我们假设检验的所有P值都低于0.05的事实是一致的。
#单因素方差分析的结果总结
最后，我们可以以总结发现的方式报告单因素方差分析的结果：
采用单因素方差分析来检验运动计划对体重减轻的影响（以磅为单位）。三种方案的减肥效果差异有统计学意义(F(2，87)=30.83,p=7.55e-11)。进行TukeyHSD事后（post hoc）试验。
方案C参与者的平均体重下降显著高于方案B参与者的平均体重下降(p<0.0001)。
方案C参与者的平均体重减轻显著高于方案A参与者的平均体重减轻(p<0.0001)。
此外，方案B参与者的平均体重减轻显著高于方案A参与者的平均体重减轻(p=0.01)。
参考：R
参考：How to Conduct a One-Way ANOVA in R
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
