【高级算法】单纯形法求解线性规划问题（C++实现）

最新推荐文章于 2024-09-21 17:36:18 发布

牧之丶

最新推荐文章于 2024-09-21 17:36:18 发布

阅读量4w

点赞数 27

分类专栏：高级算法文章标签：单纯形法线性规划高级算法 c++ 约束

本文链接：https://blog.csdn.net/zhoubin1992/article/details/46916429

版权

本文介绍了如何使用单纯形法解决线性规划问题，并详细阐述了算法原理和标准形式的转换。还提供了C++代码实现，用于求解具体的线性规划实例。

摘要由CSDN通过智能技术生成

转载请注明出处：http://blog.csdn.net/zhoubin1992/article/details/46916429

1 单纯形法

（1）单纯形法是解线性规划问题的一个重要方法。
其原理的基本框架为：
第一步：将LP线性规划变标准型，确定一个初始可行解（顶点）。
第二步：对初始基可行解最优性判别，若最优，停止；否则转下一步。
第三步：从初始基可行解向相邻的基可行解（顶点）转换，且使目标值有所改善—目标函数值增加，重复第二和第三步直到找到最优解。
（2）用程序进行运算前，要将目标函数及约束方程变成标准形式。
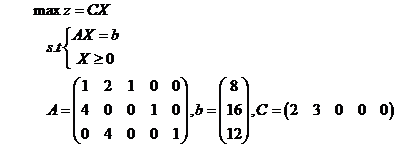
这里写图片描述
于非标准形式须作如下变换：
a) 目标函数为极小值min z=CX时，转换为max z=-CX形式；
b) 在约束方程中有 “≤”时，在加上一个松弛变量；
c) 在约束方程中有 “≥”时，采用减去一个松弛变量，再加上一个人工变量；
d) 在约束方程中有 “=”时，加上一个人工变量；
e) 所有的人工变量，松弛变量的目标函数系数置为0。
（3）对于标准形式的线性规划问题。用单纯形法计算步骤的框图。

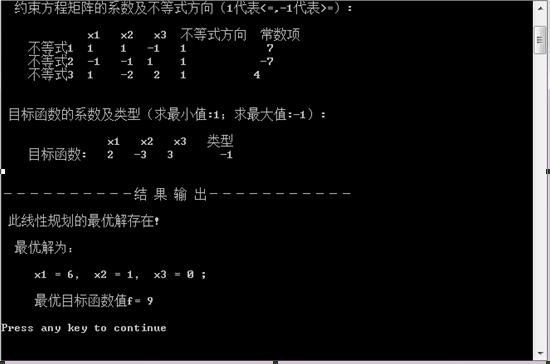
2 程序测试及结果：

线性规划问题如下:
max z=2*x1-3*x2+3x3;
x1+ x2 -x3<=7;
x1- x2 +x3<=-7;
x1-2*x2 +2*x3<=4;
x1,x2,x3>=0;

这里写图片描述

3 C++实现代码

// Simplex.cpp : 定义控制台应用程序的入口点。
//
//
/********************************* 
----------------------------------- 
单纯形法求解线性规划问题（C++实现代码）
----------------------------------- 
Author:牧之丶  Date：2014年
Email:bzhou84@163.com 
**********************************/  
#include "stdafx.h"
#include<iostream> 
#include<math.h> 
using namespace std;
#define M 10000        //全局变量大M
 float juzhen[11][31];//核心矩阵表 
 int m=0,n=0,t=0;//m:结构向量的个数 //n:约束不等式个数  //t:目标函数类型：－1代表求求最小值，1代表求最大值                          
void input() //输入接口函数
{   
    int i,j; 
    cout<<"－－－－－－－－－－单纯形法的参 数 输 入－－－－－－－－－－－"<<endl; 
    cout<<"请按提示输入下列参数："<<endl<<endl; 
    cou