欧拉四面体公式

最新推荐文章于 2019-06-28 19:25:37 发布

zhoufenqin

最新推荐文章于 2019-06-28 19:25:37 发布

阅读量3.2k

点赞数

分类专栏：计算几何

计算几何专栏收录该内容

1 篇文章 0 订阅

订阅专栏

转自http://blog.csdn.net/archibaldyangfan/article/details/8035332

1，建立x，y，z直角坐标系。设A、B、C少拿点的坐标分别为(a1,b,1,c1),(a2,b2,c2),(a3,b3,c3),四面体O-ABC的六条棱长分别为l，m，n，p，q，r；

2，四面体的体积为，由于现在不知道向量怎么打出来，我就插张图片了，

因为：V=1/3SH=1/3*(1/2)a*b*H=1/6*(a×b)·c
将这个式子平方后得到：

3，根据矢量数量积的坐标表达式及数量积的定义得

又根据余弦定理得

4，将上述的式子带入（1），就得到了传说中的欧拉四面体公式

美丽的公式

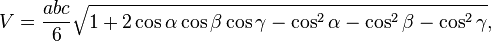
$V = \frac {abc} {6} \sqrt{1 + 2\cos{\alpha}\cos{\beta}\cos{\gamma}-\cos^2{\alpha}-\cos^2{\beta}-\cos^2{\gamma}}, \,$

海伦公式形态的四面体体积公式[编辑]

如果U、V、W、u、v、w是四面体的六条边长（U、V、W构成四面体的其中一个三角形面，而u是与U相对的棱，v是与V相对的棱，w是与W相对的棱），则四面体体积^[2]

$V = \frac{\sqrt {\,( - a + b + c + d)\,(a - b + c + d)\,(a + b - c + d)\,(a + b + c - d)}}{192\,u\,v\,w}$

这里

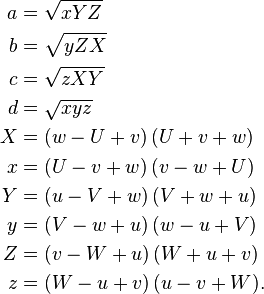
$\begin{align} a & = \sqrt {xYZ} \\ b & = \sqrt {yZX} \\ c & = \sqrt {zXY} \\ d & = \sqrt {xyz} \\ X & = (w - U + v)\,(U + v + w) \\ x & = (U - v + w)\,(v - w + U) \\ Y & = (u - V + w)\,(V + w + u) \\ y & = (V - w + u)\,(w - u + V) \\ Z & = (v - W + u)\,(W + u + v) \\ z & = (W - u + v)\,(u - v + W).\end{align}$

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
欧拉四面体公式

转自http://blog.csdn.net/archibaldyangfan/article/details/80353321，建立x，y，z直角坐标系。设A、B、C少拿点的坐标分别为(a1,b,1,c1),(a2,b2,c2),(a3,b3,c3),四面体O-ABC的六条棱长分别为l，m，n，p，q，r；2，四面体的体积为，由于现在不知道向量怎么打出来，我就插张
复制链接

扫一扫

专栏目录

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。