2016-8-9夏令营总结(网络流—增广路+dinic)

今天我们学习了一个新的一个算法：网络流。
网络流其实就是最大流。在一个有向图中，每条边的边权就是每条边的能通过的最大流量，问从源点到汇点的最大流量是多少？

增广路

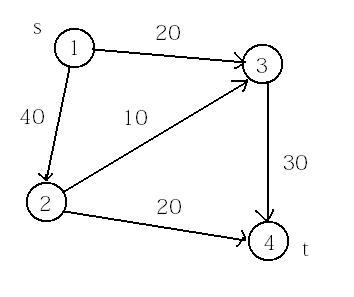
我们看看这个图，源点是s，汇点是t。如果我们一开始还不会网络流算法的话，或许我们会想到的是：每次都找一条容量最大的路径。比如我们先把1-3-4的路径搜了，然后把他们的容量全部减去20，然后再搜最大的1-2-4，把容量减去20，然后1-2-3-4，容量减去10，总流量就是50.
但是这个很明显的并不严谨，我们可以找到反例来推翻它。

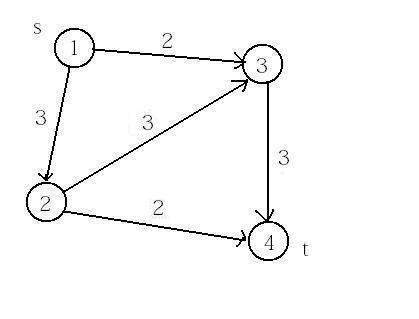
看这个图：如果我们每次找流量最大的，那会先搜到1-2-3-4，把容量减去3，然后就没有路径可以走了，那么总流量是3。可是实际上我们走1-3-4和1-2-4，那样总流量就是4.所以这个贪心的方法是错的。

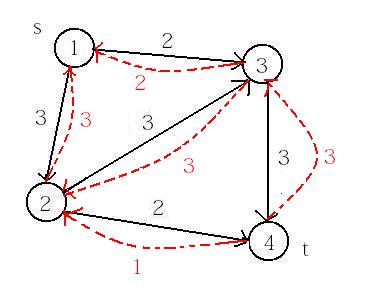
我们在上面贪心的过程中，发现一开始走完1-2-3-4，搜1-3的时候，发现2-3传过来了3个流量。那么我们能不能用这1-3的2个流量把2-3传过来3个流量的从3-2反向挤回去呢？我们有2个流量，就把2-3的2个流量挤回去然后用1-3的这2个流量顶替2-3的2个流量继续走，那么也就意味着2-3只流了1个流量，剩下的流量就可以走2-4了。那么就把每一个流量都尽量地利用回来。
其实上面的操作，就类似于讲1-3的两个流量通过3-2反向地流过去，所以我们就可以在3个流量从2-3流过时增加1条反向弧，这条反向弧的容量就是从2-3流过去的流量数。
那么整个流程就是这样的：每次都找一条可以到汇点的路径搜过去（可包含反向弧），当我们流过一条边时，假设流量为从，那么我们把它的容量减去c，它的反向弧的容量增加c（如果这条边是反向弧，那么它原来的边就是这条反向弧的反向弧）。直到找不到一条路径能流流量到汇点的时候，这个方案就是最优方案。
这就是最简单的解决网络流的方法。

最短增广路

最短增广路是增广路的优化，其实它们相差不大。因为我们在搜索一条路径时，为了尽量减少时间，我们要尽量每次都找最短的。我们建立一个层次网络，每一个点的层次就是这个点到源点的最短距离。那么我们每次第i层的点搜索时，就要搜第i+1层的点，这样就能保证每次搜的都是最短的路径，时间会尽量地减少。
所以我们每次先用bfs把每一个点的层次给算出来，同时判断能否到达汇点。如果到不了汇点，就代表已经没有增广路，所以当前总流量就是最后的总流量。如果还有路径到达汇点，那么我们就dfs搜索路径，每一次都只搜当前点的下一层的点，并且注意维护反向弧，搜到汇点之后就退出，继续下一次的bfs。
那么这个时间复杂度是多少呢？我们知道每一次dfs都会至少删掉一条边（就是会把路径中容量最小的边填满），所以bfs的次数最多是m次。根据用最短路径不断搜，最坏情况下是o(n*m)次（可证明，但我不会）。所以最短增广路的时间复杂度o(nm^2)。

dinic算法

dinic算法其实是最短增广路的优化。它们两个的不同之处在于，最短增广路每次bfs建图只可以单次增广，而dinic算法可以一次bfs建图多次增广。最短增广路是搜到一条到汇点的路径就停止，而dinic算法是搜一个点时，会尽量利用传进来的流量把他所连到的边尽量填满。也就是说每次bfs的构造层次网络，基本都可以删掉一个点，所以会bfs大约n次左右，所以总时间复杂度为o(n^2*m).

模版题：POJ1273

题目大意：
现在有m个池塘(从1到m开始编号,1为源点,m为汇点),及n条水渠,给出这n条水渠所连接的池塘和所能流过的水量,求水渠中所能流过的水的最大容量。
n,m<=200，保证所有结果在int范围内，多组数据。
题目分析：
这题很明显是网络流，由于数据较小，我们可以使用增广路，也可以用dinic算法。
参考代码：
增广路：

#include <iostream>
#include <fstream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;

struct Tline
{ int x,y,v; };
Tline l[407];
int n,m;
vector<int> line[207][207];
bool f[207];
int ans,minn,fl=1;

bool dfs(int k)
{
    if(k==m)
    {
        ans+=minn;
        return true;
    }
    f[k]=1;
    for(int i=1;i<=m;i++)
    {
        if(!line[k][i].size()) continue;
        for(int j=0;j<line[k][i].size();j++)
        {
            int y=line[k][i][j];
            if(l[y].v==0 || f[i]) continue;
            minn=min(minn,l[y].v);
            if(dfs(i))
            {
                int tmp=l[y].v;
                l[y].v-=minn;
                l[y^1].v+=minn;
                return true;
            }
        }
    }
    return false;
}

int main()
{
    scanf("%d%d",&n,&m);
    while(1)
    {
        fl=0;
        memset(l,0,sizeof(l));
        for(int i=1;i<=m;i++)
            for(int j=1;j<=m;j++)
                line[i][j].clear();
        int x,y,v;
        for(int i=0;i<n;i++)
        {
            scanf("%d%d%d",&x,&y,&v);
            l[fl].x=x;
            l[fl].y=y;
            l[fl].v=v;
            line[x][y].push_back(fl);
            fl++;
            l[fl].x=y;
            l[fl].y=x;
            line[y][x].push_back(fl);
            fl++;
        }
        memset(f,0,sizeof(f));
        ans=0;
        minn=100000000;
        for(;dfs(1);)
        {
            minn=100000000;
            memset(f,0,sizeof(f));
        }
        printf("%d\n",ans);
        n=-1;
        scanf("%d%d",&n,&m);
        if(n==-1) break;
    }

    return 0;
}

dinic算法：

#include <iostream>
#include <fstream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;


const int maxN=200100;
const int maxM=500100;
const int oo=100000000;
struct Tline
{ int x,y,c; };
Tline line[maxM];
struct Tnode
{ int t,l; };
vector<Tnode> node[maxN];
int n,m;
int que[maxN],level[maxN];
int lnum=0;
long long Max=0;

bool bfs(int s,int t)   //构造新的层次网络 level表示第几层 
{
    memset(level,0,sizeof(level));
    int head=0,tail=1;
    level[s]=1;
    que[head]=s;
    for(;head<tail;head++)
    {
        int u=que[head];
        if(u==t) return true;
        for(int i=0;i<node[u].size();i++)
        {
            int v=node[u][i].t;
            int l=node[u][i].l;
            if(!level[v] && line[l].c)
            {
                level[v]=level[u]+1;
                que[tail++]=v;
            }
        }
    }
    return false;
}

int dfs(int u,int t,int c)
{
    if(u==t) return c;
    int ret=0;
    for(int i=0;i<node[u].size();i++)
    {
        int v=node[u][i].t,l=node[u][i].l;
        if(level[v]==level[u]+1 && line[l].c)
        {
            int Min=min(c-ret,line[l].c);
            int tmp=dfs(v,t,Min);
            line[l].c-=tmp;
            line[l^1].c+=tmp;
            ret+=tmp;
            if(ret==c) return ret;  //dinic多次增广 
        }
    }
    return ret;
}

int main()
{
    scanf("%d%d",&m,&n);
    while(1)
    {
        lnum=0;
        int x,y,c;
        Tnode tmp;
        for(int i=1;i<=n;i++)
            node[i].clear();
        memset(line,0,sizeof(line));
        for(int i=0;i<m;i++)
        {
            scanf("%d%d%d",&x,&y,&c);
            tmp.t=y;tmp.l=lnum;
            node[x].push_back(tmp);
            line[lnum].x=x;
            line[lnum].y=y;
            line[lnum].c=c;
            lnum++;
            tmp.t=x;tmp.l=lnum;
            node[y].push_back(tmp);
            line[lnum].x=y;
            line[lnum].y=x;
            line[lnum].c=0;
            lnum++;
        }
        int s=1,t=n;
        long long ans=0;
        while(bfs(s,t)) ans+=dfs(s,t,oo);
        printf("%d\n",ans);
        n=-1;
        scanf("%d%d",&m,&n);
        if(n==-1) break;
    }

    return 0;
}