插入排序

直接插入排序是利用顺序查找来判断带插入元素r[i]在r[1] ~ r[i - 1]有序序列中的位置，将r[i]与前面的记录的r[1] ~ r[i - 1]从后向前比较，将所有大于r[i]的元素后移一位，直到遇到一个小于或等于r[i]的元素，该元素位置就是r[i]插入的位置 。现在按照这个过程执行一遍

比如无序数组 33、12、25、33、68、19、80

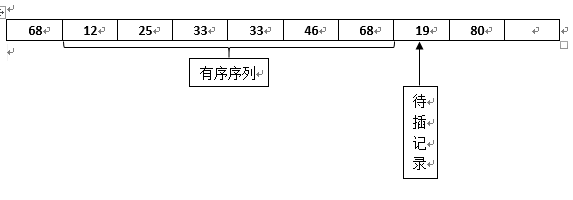
初始状态

首先选择第二个元素作为待插记录，也就是12，放到第一位待插元素上，然后和它前面的元素进行比较，如果遇到比它大的就交换顺序，直到找到一个小于等于它的，所以第一趟比完之后就是下面的状态

第一趟完成之后，待插元素下标后移一位，也就是25，然后用25和它前面的元素进行比较，如果遇到比它大的就交换顺序，直到找到一个小于等于它的，所以第二趟比完之后的状态

第二趟完成之后，待插元素下标后移一位，也就是46，然后与46前面的元素进行比较，如果遇到比它大的就交换顺序，直到找到一个小于等于它的，所以第三趟比完之后的状态

第三趟完成之后，待插元素下标后移一位，也就是33，然后与33前面的元素进行比较，如果遇到比它大的就交换顺序，直到找到一个小于等于它的，所以第四趟比完之后的状态

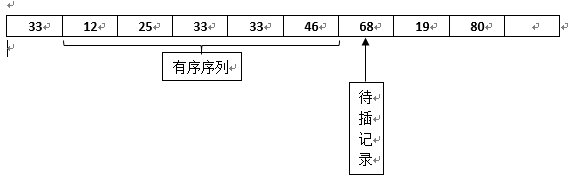
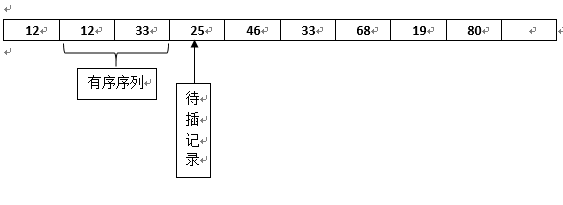
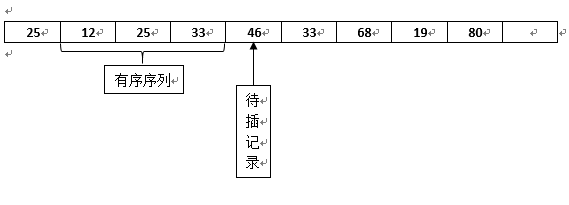
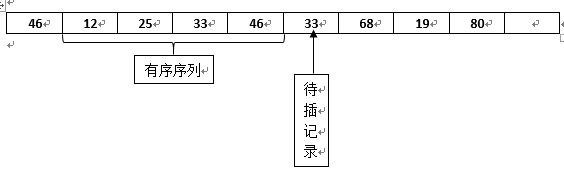
注意这一次比较中的33和之前的33的相对位置并没有发生改变，所以插入排序是稳定的，接着继续比较，第五趟比完之后的状态

接着继续比较，19和它前面的元素比较，直到遇到小于等于19的，所以第六趟比完后的状态

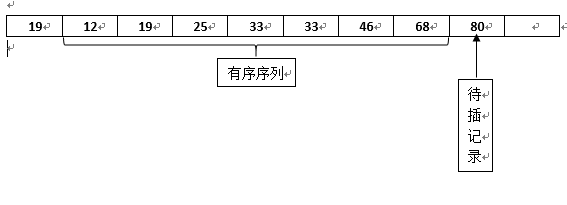
继续比较，最后一趟完成后的状态

到这整个插入排序的过程就结束了，下面看一下代码实现，其实过程懂了代码很容易写出来

    public static void insertSort(int [] l){
        if(l != null && l.length != 0){
            for (int i = 2; i < l.length; i++) {
                l[0] = l[i];
                int j;
                for (j = i - 1; l[0] < l[j]; j--){
                    l[j + 1] = l[j];
                }
                l[j + 1] = l[0];
            }
        }
    }

仔细观察我们会发现，在第三趟、第五趟和第七趟的比较过程中当前待插记录元素已经是最大的元素了，所以既不需要在进行比较了，于是乎我们可以将算法改进一下

    public static void insertSort(int [] l){
        if(l != null && l.length != 0){
            for (int i = 2; i < l.length; i++) {
                if(l[i] < l[i - 1]){
                    l[0] = l[i];
                    int j;
                    for (j = i - 1; l[0] < l[j]; j--){
                        l[j + 1] = l[j];
                    }
                    l[j + 1] = l[0];
                }
            }
        }
    }

在每一趟进行比较之前都判断当前待插元素和之前的最大值进行比较，如果待插元素小的话在进行插入操作，现在这个算法的效率已经相当不错了，但是在确定插入位置时是按照顺序查找来确定的，我们可以通过折半查找来确定插入位置，改进后的代码如下

    public static void insertSort(int [] l){
        if(l != null && l.length != 0){
            int j;
            int low, high, mid;
            for (int i = 2; i < l.length; i++) {
                if(l[i] < l[i - 1]){
                    l[0] = l[i];
                    low = 1; high = i - 1;
                    while (low <= high){
                        mid = (low + high)/2;
                        if(l[0] < l[mid]){
                            high = mid - 1;
                        } else {
                            low = mid + 1;
                        }
                    }
                    for(j = i - 1; j >= low; j--){
                        l[j + 1] = l[j];
                    }
                    l[low] = l[0];
                }
            }
            System.out.println(Arrays.toString(l));
        }
    }

到这我们就把插入排序做到最大程度的优化了。插入排序空间复杂度O(1)，只需要借助一个辅助元素， 时间复杂度最好情况下O(n)，最坏条件下O(n^2) ，而且插入排序是稳定的，相等元素的相对位置不会改变。插入排序适用于基本有序的序列。