761. Special Binary String

Special binary strings are binary strings with the following two properties:

• The number of 0's is equal to the number of 1's.
• Every prefix of the binary string has at least as many 1's as 0's.

  Given a special string S, a move consists of choosing two consecutive, non-empty, special substrings of S, and swapping them. (Two strings are consecutive if the last character of the first string is exactly one index before the first character of the second string.)

  At the end of any number of moves, what is the lexicographically largest resulting string possible?

  Example 1:
  

  Input: S = "11011000"
  Output: "11100100"
  Explanation:
  The strings "10" [occuring at S[1]] and "1100" [at S[3]] are swapped.
  This is the lexicographically largest string possible after some number of swaps.
  

  Note:

  1. S has length at most 50.
  2. S is guaranteed to be a special binary string as defined above.
  
  

  Just 4 steps:

  1. Split S into several special strings (as many as possible).
  2. Special string starts with 1 and ends with 0. Recursion on the middle part.
  3. Sort all special strings in lexicographically largest order.
  4. Join and output all strings.

  Updated:

  The middle part of a special string may not be another special string. But in my recursion it is.
  For example, 1M0 is a splitted special string. M is its middle part and it must be another special string.

  Because:

  1. The number of 0's is equal to the number of 1's in M
  2. If there is a prefix P of Mwhich has one less 1's than 0's, 1P will make up a special string. 1P will be found as special string before 1M0 in my solution.
     It means that every prefix of M has at least as many 1's as 0's.

  Based on 2 points above, M is a special string.

  注意：尽量拆分成小的，因为用小的可以组合成大的，那多个小的效果一定比大的要好

  class Solution:
      def makeLargestSpecial(self, S):
          """
          :type S: str
          :rtype: str
          """
          l, cnt, i = [], 0, 0
          for j, v in enumerate(S):
              cnt = cnt+1 if v=='1' else cnt-1
              if cnt == 0: # to make Special as small as possible
                  l.append('1' + self.makeLargestSpecial(S[i+1:j]) + '0') # first must be 1, last must be 0
                  i = j + 1
          return ''.join(sorted(l)[::-1])
      
  s=Solution()
  print(s.makeLargestSpecial('11011000'))

  
  有人理解为括号组合

  According to the description , there are 2 requirement for Special-String

  1. The number of 0's is equal to the number of 1's.
  2. Every prefix of the binary string has at least as many 1's as 0's.

  The 2nd definition is essentially saying that at any point of the string, you cannot have more 0's than 1's.

  If we map '1' to '(', '0's to ')', a Special-String is essentially Valid-Parentheses, therefore share all the properties of a Valid-Parentheses
  A VP (Valid-Parentheses) have 2 form:

  1. single nested VP like "(())", or "1100";
  2. a number of consecutive sub-VPs like "()(())", or "101100", which contains "()" + "(())" or "10" + "1100"

  And this problem is essentially ask you to reorder the sub-VPs in a VP to make it bigger. If we look at this example : "()(())" or "101100", how would you make it bigger?
  Answer is, by moving the 2nd sub-string to the front. Because deeply nested VP contains more consecutive '('s or '1's in the front. That will make reordered string bigger.

  The above example is straitforward, and no recursion is needed. But, what if the groups of sub-VPs are not in the root level?
  Like if we put another "()(())" inside "()(())", like "()(( ()(()) ))", in this case we will need to recursively reorder the children, make them MVP(Max-Valid-Parentheses), then reorder in root.

  To summarize, we just need to reorder all groups of VPs or SS's at each level to make them MVP, then reorder higher level VPs;

  class Solution {
  public:
      string makeLargestSpecial(string s) {
          int i = 0;
          return dfs(s, i);
      }
  
  private:
      string dfs(string& s, int& i) {
          string res;
          vector<string> toks;
          while (i < s.size() && res.empty()) {
              if (s[i++] == '1') toks.push_back(dfs(s, i));
              else res += "1";
          }
          bool prefix = res.size();
          sort(toks.begin(), toks.end());
          for (auto it = toks.rbegin(); it != toks.rend(); it++) res += *it;
          if (prefix) res += '0';
          return res;
      }
  };

  有人理解为mountains

  Intuition

  We can represent binary strings as "up and down" drawings, as follows:

  

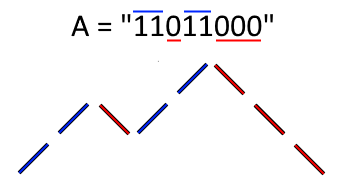
  In such a drawing, "1" is a line up one unit, and "0" is a line down one unit, where all lines are 45 degrees from horizontal.

  Then, a binary string is special if and only if its up and down drawing does not cross below the starting horizontal line.

  Now, say a special binary string is a mountain if it has no special proper prefix. When viewed through the lens of up and down drawings, a special binary string is a mountain if it touches the starting horizontal line only at the very beginning and the very end of the drawing. Notice that every special string can be written as consecutive mountains.

  Without loss of generality, we can assume we only swap mountains. Because if we swap special adjacent substrings A and B, and A has mountain decomposition  A=M1M2…Mk A=M1M2…Mk, then we could instead swap $B$and M_kM​k​​, then $B$ and M_{k-1}M​k−1​​, and so on.

  Also, if $S$ has mountain decomposition  S=M1M2…Mk S=M1M2…Mk, and we choose $A$ to start not at the start of some M_iM​i​​, then $A$ has global height $h>0$, and so $A$ cannot be special if it includes parts of another mountain M_{i+1}M​i+1​​ as the end of mountain M_iM​i​​ will cause it to dip to global height $0<h$.

  Algorithm

  Say F(String S) is the desired makeLargestSpecial function. If S has mountain decomposition  S=M1M2…Mk S=M1M2…Mk, the answer is  reverse_sorted(F(M1),F(M2),…,F(Mk)) reverse_sorted(F(M1),F(M2),…,F(Mk)), as swaps A, Binvolving multiple M_iM​i​​ cannot have A or B start differently from where these M_iM​i​​ start.

  It remains to determine how to handle the case when  S=S0,S1,…,SN−1 S=S0,S1,…,SN−1 is a mountain. In that case, it must start with "1" and end with "0", so the answer is "1" + F([S[1], S[2], ..., S[N-2]]) + "0".