矩阵乘法，整除，同余，GCD,LCM

 矩阵乘法是线性代数的内容，但在考察数学的算法题中也会出现。

每一个矩阵都有行数与列数，只有当两个相乘的矩阵的左矩阵的列数等于右矩阵的行数时，才能做矩阵乘法，否则不能。例如3*5的矩阵可以与5*7的矩阵相乘，得到3*7的矩阵

具体实现为

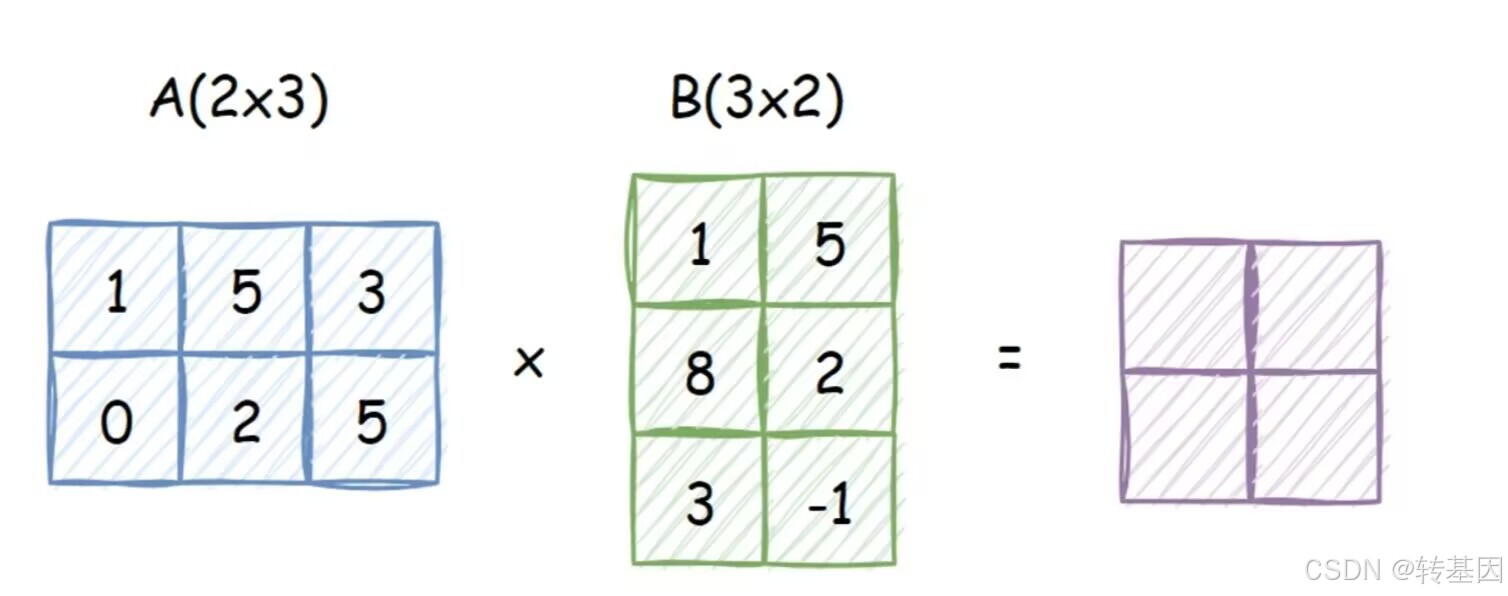
假设新得到的矩阵为C,那C(1,1)的值就为1*1+5*8+3*3，即将对应数位相乘再相加，得到的新矩阵C的规模是2*2

例题蓝桥1550矩阵相乘,AC代码附上

#include <iostream>
using namespace std;
const int N=105;
int a[N][N],b[N][N],c[N][N];
int main()
{
  ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
  int n,m,k;cin>>n>>m>>k;
  for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)cin>>a[i][j];

    for(int i=1;i<=m;i++)
      for(int j=1;j<=k;j++)cin>>b[i][j];

      for(int i=1;i<=n;i++)
      {
        for(int j=1;j<=k;j++)
        {
          for(int t=1;t<=m;t++)
          {
            c[i][j]+=a[i][t]*b[t][j];
          }
          cout<<c[i][j]<<" ";
        }
        cout<<endl;
      }
  return 0;
}

整除;

在计算机中，整数之间的除法通常是向下取整的，例如12/5==2, 那要相上取整呢？只需将式子改成(12+5-1)/5,假定x/y要向上取整，可以写为(x+y-1)/y或(x-1)/y+1

如果x可以被y整除，记做y|x,例4|12,7|21

同余：

当两个或多个数字，对于一个模数M的余数是相等的，或者说在模M的意义下相等，就叫同余

例如20和10在模5的意义下是相等的，都为0

 

GCD(最大公约数)

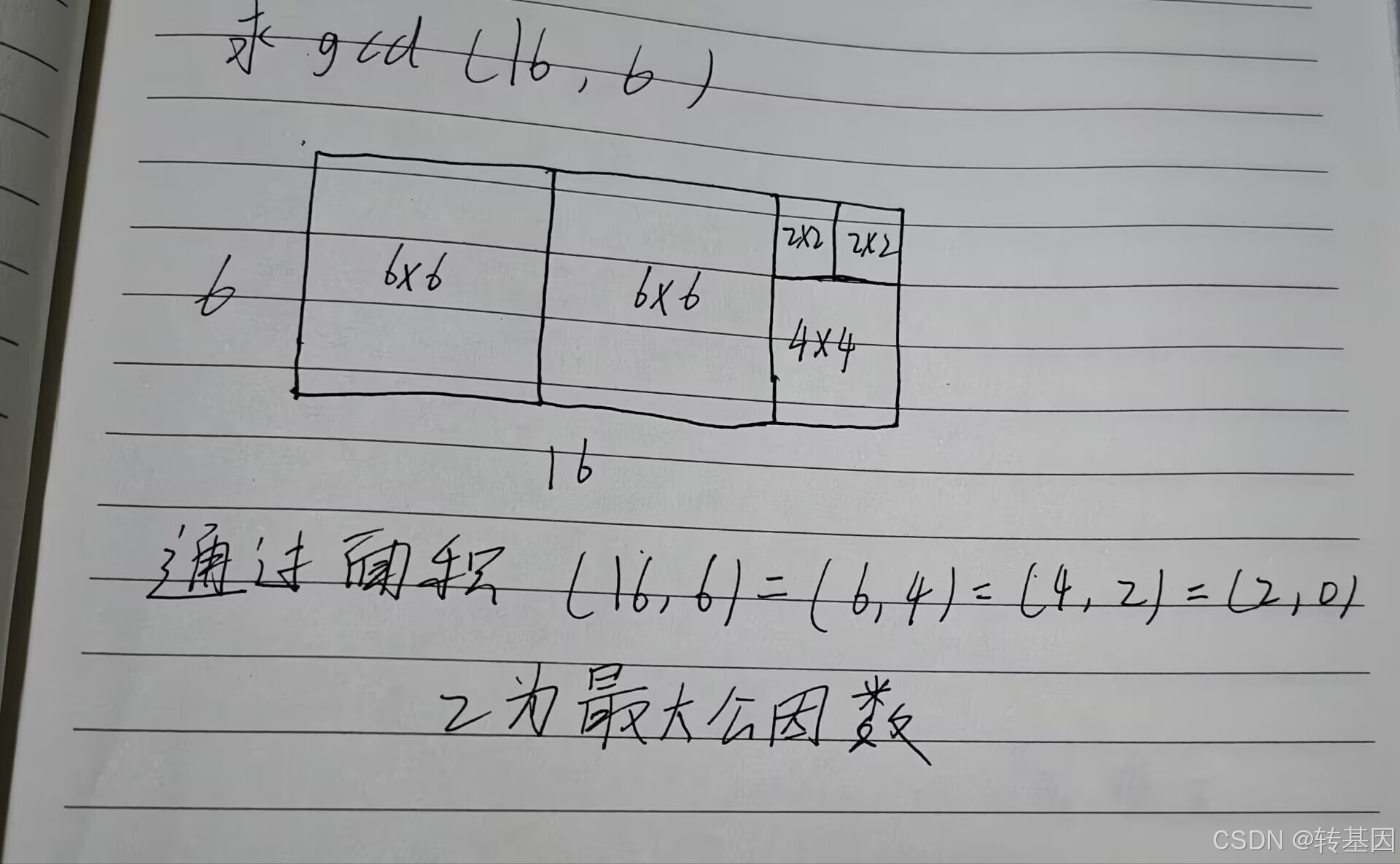
gcd通过欧几里德的辗转相除法来得到，记为a和b的最大公约数等b和a%b的最大公约数，可以不断辗转相除直到a%b等于0时，b就为最大公约数。

那么如何来证明呢 ？

以下给出图解和数学证明

 

代码如何实现呢？

来看蓝桥1260最大公约数

AC代码附上

#include <bits/stdc++.h>
using namespace std;
int gcd(int a,int b)
{
  return b==0?a:gcd(b,a%b);
}
int main()
{
  ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
  int t;cin>>t;
  while(t--)
  {
  int a,b;cin>>a>>b;
  cout<<gcd(a,b)<<endl;
  }
  return 0;
}

 LCM(最小公倍数)怎么求呢

其实有lcm=a*b/gcd(a,b)就可以直接求

模板

int lcm(int a,int b)
{
   return a/gcd(a,b)*b;
}

这里推荐先做除法，避免溢出

除此以外，c++库中有专门计算gcd和lcm的函数，在algorithm头文件里

只需调用__gcd(a,b)和__lcm(a,b)就可以啦