- 前序(先序)遍历
- 中序遍历
- 后续遍历
- 层序遍历
如图二叉树:
二叉树结点结构
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x){
val=x;
}
@Override
public String toString(){
return "val: "+val;
}
}访问函数
public void visit(TreeNode node){
System.out.print(node.val+" ");
}前序遍历
对于图中二叉树而言其前序遍历结果为:6 2 0 1 4 5 8 9
二叉树的前序遍历即先遍历根结点再遍历左结点最后遍历右结点,使用递归如下:
/**
* 递归先序遍历
* */
public void preOrderRecursion(TreeNode node){
if(node==null) //如果结点为空则返回
return;
visit(node);//访问根节点
preOrderRecursion(node.left);//访问左孩子
preOrderRecursion(node.right);//访问右孩子
}非递归:
利用栈来实现二叉树的先序非递归遍历
/**
* 非递归先序遍历二叉树
* */
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> resultList=new ArrayList<>();
Stack<TreeNode> treeStack=new Stack<>();
if(root==null) //如果为空树则返回
return resultList;
treeStack.push(root);
while(!treeStack.isEmpty()){
TreeNode tempNode=treeStack.pop();
if(tempNode!=null){
resultList.add(tempNode.val);//访问根节点
treeStack.push(tempNode.right); //入栈右孩子
treeStack.push(tempNode.left);//入栈左孩子
}
}
return resultList;
}更新:评论里有人说不理解非递归的先序遍历,其实你举个例子,然后画个图就可以理解了,以上图中的二叉树为例,先将6入栈,此时List为空,Stack只有一个元素6,进入while循环,弹出栈顶加入List,将6的右孩子和左孩子入栈,此时Stack从栈底到栈顶元素为8,2,List元素为6,由于栈不为空,进入while循环,弹出栈顶2,将2加入List,同时将2的右孩子和左孩子分别入栈,此时Stack从栈底到栈顶的元素为8,4,0, List的元素为6,2,由于栈不为空再次进入while循环…依次下去,弹出0加入List,入栈1,null,此时Stack从栈底到栈顶为8,4,1,null,List为6,2,0,弹出null为空继续弹出1,如此下去就可以了…
中序遍历
对于二叉树的中序遍历,即先访问左结点再访问根节点最后访问右结点
递归方法如下:
/**
* 递归中序遍历
* */
public void preOrderRecursion(TreeNode node){
if(node==null) //如果结点为空则返回
return;
preOrderRecursion(node.left);//访问左孩子
visit(node);//访问根节点
preOrderRecursion(node.right);//访问右孩子
}非递归:
在上图中的二叉树,其中序遍历为:0 1 2 4 5 6 8 9
可以看到,二叉树的中序遍历如下:
先将根节点入栈,
一直往其左孩子走下去,将左孩子入栈,直到该结点没有左孩子,则访问这个结点,如果这个结点有右孩子,则将其右孩子入栈,重复找左孩子的动作,这里有个要判断结点是不是已经被访问的问题。
非递归中序遍历(效率有点低),使用map(用set貌似更合理)来判断结点是否已经被访问
leetcode地址:https://leetcode.com/problems/binary-tree-inorder-traversal/
/**
* 非递归中序遍历
* */
public List<Integer> inorderTraversalNonCur(TreeNode root) {
List<Integer> visitedList=new ArrayList<>();
Map<TreeNode,Integer> visitedNodeMap=new HashMap<>();//保存已访问的节点
Stack<TreeNode> toBeVisitedNodes=new Stack<>();//待访问的节点
if(root==null)
return visitedList;
toBeVisitedNodes.push(root);
while(!toBeVisitedNodes.isEmpty()){
TreeNode tempNode=toBeVisitedNodes.peek(); //注意这里是peek而不是pop
while(tempNode.left!=null){ //如果该节点的左节点还未被访问,则需先访问其左节点
if(visitedNodeMap.get(tempNode.left)!=null) //该节点已经被访问(不存在某个节点已被访问但其左节点还未被访问的情况)
break;
toBeVisitedNodes.push(tempNode.left);
tempNode=tempNode.left;
}
tempNode=toBeVisitedNodes.pop();//访问节点
visitedList.add(tempNode.val);
visitedNodeMap.put(tempNode, 1);//将节点加入已访问map
if(tempNode.right!=null) //将右结点入栈
toBeVisitedNodes.push(tempNode.right);
}
return visitedList;
}Discuss中有人给出更简洁的方法:https://leetcode.com/discuss/19765/iterative-solution-in-java-simple-and-readable
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode cur = root;
while(cur!=null || !stack.empty()){
while(cur!=null){
stack.add(cur);
cur = cur.left;
}
cur = stack.pop();
list.add(cur.val);
cur = cur.right;
}
return list;
}后序遍历
递归代码就不贴了
如果之前的非递归中序遍历使用map的方法理解后,后序遍历的话我们也可以使用一个map来保存那些已经被访问的结点,后序遍历即先访问左孩子再访问右孩子最后访问根结点。
非递归代码:
/**
* 非递归后序遍历
* */
public List<Integer> postOrderNonCur(TreeNode root){
List<Integer> resultList=new ArrayList<>();
if(root==null)
return resultList;
Map<TreeNode,Integer> visitedMap=new HashMap<>();
Stack<TreeNode> toBeVisitedStack=new Stack<>();
toBeVisitedStack.push(root);
while(!toBeVisitedStack.isEmpty()){
TreeNode tempNode=toBeVisitedStack.peek(); //注意这里是peek而不是pop
if(tempNode.left==null && tempNode.right==null){ //如果没有左右孩子则访问
resultList.add(tempNode.val);
visitedMap.put(tempNode, 1);
toBeVisitedStack.pop();
continue;
}else if(!((tempNode.left!=null&&visitedMap.get(tempNode.left)==null )|| (tempNode.right!=null && visitedMap.get(tempNode.right)==null))){
//如果节点的左右孩子均已被访问
resultList.add(tempNode.val);
toBeVisitedStack.pop();
visitedMap.put(tempNode, 1);
continue;
}
if(tempNode.left!=null){
while(tempNode.left!=null && visitedMap.get(tempNode.left)==null){//左孩子没有被访问
toBeVisitedStack.push(tempNode.left);
tempNode=tempNode.left;
}
}
if(tempNode.right!=null){
if(visitedMap.get(tempNode.right)==null){//右孩子没有被访问
toBeVisitedStack.push(tempNode.right);
}
}
}
return resultList;
}leetcode地址:https://leetcode.com/problems/binary-tree-postorder-traversal/
Discuss中有人给出了一个”巧“的方法,即先采用类似先序遍历,先遍历根结点再右孩子最后左孩子(先序是先根结点再左孩子最后右孩子),最后把遍历的序列逆转即得到了后序遍历
https://leetcode.com/discuss/101547/java-recursive-and-iterative-solutions
public List<Integer> postorderTraversal(TreeNode root) {
Deque<TreeNode> stack = new LinkedList<>();
stack.push(root);
List<Integer> ret = new ArrayList<>();
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
if (node != null) {
ret.add(node.val);
stack.push(node.left);
stack.push(node.right);
}
}
Collections.reverse(ret);
return ret;
} 层序遍历
层序遍历也即宽度优先搜索,一层一层搜索,非递归代码如下:
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> resultList=new ArrayList<>();
int levelNum=0;//记录某层具有多少个节点
Queue<TreeNode> treeQueue=new LinkedList<>();
treeQueue.add(root);
while(!treeQueue.isEmpty()){
levelNum=treeQueue.size();
List<Integer> levelList=new ArrayList<>();
while(levelNum>0){
TreeNode tempNode=treeQueue.poll();
if(tempNode!=null){
levelList.add(tempNode.val);
treeQueue.add(tempNode.left);
treeQueue.add(tempNode.right);
}
levelNum--;
}
if(levelList.size()>0)
resultList.add(levelList);
}
return resultList;
}leetcode地址:https://leetcode.com/problems/binary-tree-level-order-traversal/








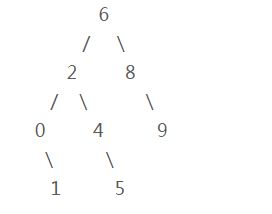

















 700
700

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










