矩阵相乘--高效实现方法

假如有两个矩阵M，N相乘，Q= M X N，M是m1 X n1矩阵， N是 m2 X n2。 只有当n1 = m2时，才可以进行两个矩阵的相乘。一般的做法是：（1）我们用两个二维数组分别存放 M 和 N ，然后再用一个二维数组 存放 Q。实现 Q = M X N的算法如下：（下标从1开始）

for( i = 1; i<= m1; ++i)

     for(j = 1; j <= n2; ++j)

    {

       Q[ i ][ j ] = 0;

       for( k = 1; k<= n1; ++k)

        Q[ i ][ j ] += M[ i ][ k ] * N[ k ][ j ];

    }

这种方法需要的内存空间是：sizeof( ElemType ) * ( m1 * n1 + m2 * n2 + m1 * n2)

时间复杂度分别是：O( m1 * n2 * n1);  

假如M和N都是稀疏矩阵（非零元素很少），我们假设M 的是 50 X 60的矩阵，非零元素为：10。 N 是 60 X 60的矩阵，非零元素为：10。因为两个元素相乘，其中一个为零结果也就为零。我们要的只是非零的数据。如果按上面那种方法，将会浪费很多空间。于是我们考虑用另一种方式存储矩阵。那就是典型的“三元组”，用个结构体表示这种存储结构。一个存行坐标，一个存列坐标。一个存它的值。这就是著名的三元组法。可以得出如果用三元组存储以前数据，需要的空间是 M 和N都只需要 10 * sizeof(struct)。比起存储 60 x 60和60 X 50的空间节省了很多。这从空间上解决了问题。两外如果用三元组方法存储数据（非零数据）也方便我们做乘法运算，减少了零元素的相乘。这不是一举两得吗。

  三元组结构：

#define  MAXSIZE  12500
struct  Triple {
     int  i, j;            //该非零元的行下标和列下标
     ElemType  e;    // 该非零元的值，ElemType表示元素的类型。如：int ,double
 } ;  // 三元组类型

 struct   TSMatrix{
     Triple  data[MAXSIZE + 1];    //把非零元的三元组对象放在一个数组中，一般我们按“以行序为主序”（顺序是先存第一行非零元，

                                                                                                                                                                            再存第二行）
      int     mu, nu, tu;                 // mu , nu ,tu 分别表示行数，列数，非零元个数
} ;  // 稀疏矩阵类型

在这里还有一个很重要的作法，因为我们把非零元素按三元组的形式存放在数组中，而且是按行序为主序存放的。所以为了方便快速知道第x行的开头在数组中第几个位置，我们引入了一个数组Cpot[]。num[]数组存的是每行非零元的个数。它用来存放每一行的开头非零元素在数组data的位置（既是下标）。作法如下 三元组M和N

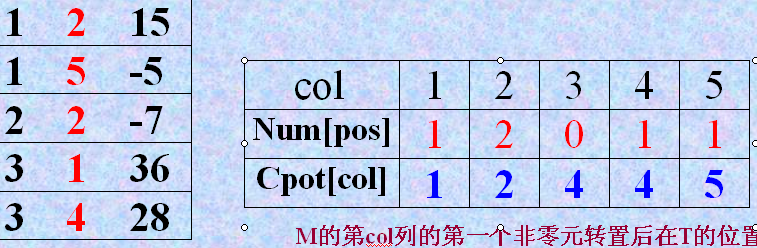
///MN的Cpot

if (M.tu) {
    for (col=1; col<=M.nu; ++col)  num[col] = 0;
    for (t=1; t<=M.tu; ++t)  ++num[M.data[t].j];

}

cpot[1] = 1;
for (col=2; col<=M.nu; ++col)
cpot[col] = cpot[col-1] + num[col-1];

N的Cpot

if (N.tu) {
    for (col=1; col<=N.nu; ++col)  num[col] = 0;
    for (t=1; t<=M.tu; ++t)  ++num[M.data[t].j];

}

cpot[1] = 1;
for (col=2; col<=N.nu; ++col)
cpot[col] = cpot[col-1] + num[col-1];

 

到这里前面要处理的步骤基本已经完成。接下来就是实现相乘的算法。下面算法有点难理解，但我们知道它的思想就够了

Status MultSMatrix (TSMatrixM, TSMatrixN, TSMatrix&Q)

{
   if (M.nu != N.mu) return ERROR;
   Q.mu = M.mu; Q.nu = N.nu; Q.tu = 0;
   if (M.tu*N.tu != 0) {   // Q是非零矩阵
      for (arow=1; arow<=M.mu; ++arow)

       {
              ctemp[] = 0;                 // 当前行各元素累加器清零
            Q.rpos[arow] = Q.tu+1;      ///为Q也弄个rpos
            for (p=M.rpos[arow]; p<M.rpos[arow+1];++p) {
   //对当前行中每一个非零元
    brow=M.data[p].j;//找到对应元在N中的行号         
    if (brow < N.nu )  t = N.rpos[brow+1];
        else  { t = N.tu+1 }
        for (q=N.rpos[brow];  q< t;  ++q) {
          ccol = N.data[q].j;            // 乘积元素在Q中列号
          ctemp[ccol] += M.data[p].e * N.data[q].e;
        } // for q
      } // 求得Q中第crow( =arow)行的非零元
      for (ccol=1; ccol<=Q.nu; ++ccol) if (ctemp[ccol]) {
        if (++Q.tu > MAXSIZE) return ERROR;
        Q.data[Q.tu] = {arow, ccol, ctemp[ccol]};
      } // 压缩存储该行非零元