原文教材 与 参考资料:
Boneh Dan , Shoup Victor . A Graduate Course in Applied Cryptography[J].
该书项目地址(可以免费获取):http://toc.cryptobook.us/
博客内容为对该书的学习笔记(包括但不限于翻译、额外绘图、注解、个人理解等),并非原创知识,仅帮助理解,整理思路.
19.6 Identification and Signatures from Sigma protocols
Sigma 协议关注的是对于“声明-证据”的关系证明,并不关心该关系的生成是如何生成的,此处,我们给Sigma协议增加一个密钥生成协议,即可得到一个通用的ID身份认证协议的构造。下面首先给出该构造是能够抵抗直接攻击(direct attacks)的。
给出安全定理描述如下:

该规约过程如下图描述:

G :密钥生成算法,负责生成一对公钥和私钥,并且该算法G是单向的,并依据此有攻击游戏19.6.
B :B是G的敌手,同时B扮演A的挑战者。
A:一个仿冒攻击敌手,能够发起直接的仿冒攻击,生成“合法”的会话。
思路: B使用重绕技术调用敌手A运行2次,最终使用知识提取器算法得到G的秘密值x`。
进一步,由于该协议可以抵抗直接攻击,显然我们可以使用先前的技术,得出其是抵抗窃听敌手的,不过是增加一些PV之间的会话给敌手A进行窃听,详细过程在之前博客中(对应本书19章前半部分内容)。

19.6.1 The Fiat-Shamir heuristic for signatures
在上文中,我们给出了Sigma+KG 可以构造一个ID认证协议,那么该ID协议转换为一个数字签名协议也是可能的并且是合理的。
下面给出一个启发式的构造:Fiat-Shamir签名协议:

1. key gen 阶段,由密钥生成算法,给出具体的公钥和私钥对。
2. sign 阶段,生成一个承诺t, 然后计算c = Hash(m,t) , 再计算得到z. 输出(t,z)即为签名,其中m是公开的。
3. verify 阶段,对上述签名进行验证。
此时,我们还不能证明该签名协议是安全的,需要做出一些往外的假设与定义:
第一个定义 承诺不可预测(Unpredictable commitments)
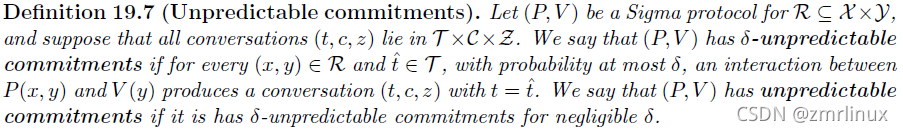
PV组成一个Sigma协议,关于关系R,并且假设存在关系R上的合法会话内容(x,y,t),则对任意的该关系R上的声明-证据,以可忽略的概率存在相同的承诺部分,t1= t2.即为承诺部分不可预测,一旦承诺部分可以预测,那么分分钟敌手获得两个相同的合法会话,然后直接运行知识提取器获得秘密值。
所以给出RO模型下,该ID协议的安全性定理:

该定理的证明过程和定理19.7 是相同的。
19.6.1-1 The GQ signature scheme
GQ ID 协议是基于RSA的一个PV协议,现在将该PV协议转换成一个签名协议,自然地,该GQ签名协议如下所述:

Set up algorithm: (n,e)是公开参数;
Key generation algorithm :生成密钥对(x,y);
Sign algorithm: 生成承诺yt, 计算c = Hash(m,yt), 签名xz.
Verify algorithm: xz^e = yt * y^c;
GQ 签名协议与RSA-FDH相比,速度更快,因为在RSA-FDH中有更多的指数运算,而c的长度在这里是比较小的,小于e-1, 一般128比特。这在一些计算能力稍弱的场景下式有用的。
19.7 Combining Sigma protocols: AND and OR proofs
sigma 协议本身也可以当做是一种组件,使用其可以组织新的sigma协议。
在AND-proof 中,证明者可以向验证者证明其掌握了一对声明的证据。
在OR-proof中,证明者可以向验证者证明其掌握了两个声明中的一个的证据。
19.7.1 The AND-proof construction
存在两个关系R1和R0,其使用相同的挑战空间c.
描述如下:

所以可以使用一个新的sigma协议构造出一个新的R“AND”关系证明协议:
AND-R 描述如下:
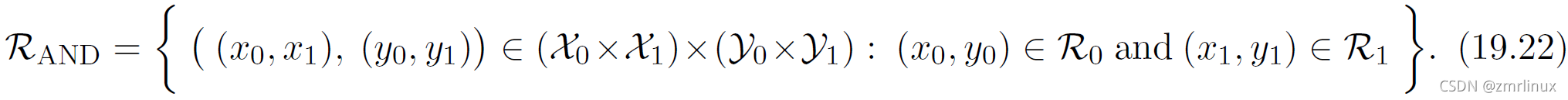
新协议运行过程如下:

显然,有以下的安全定理,通过组件的知识合理性与HVZK,我们可以推定,新的协议具备HVZK属性与知识合理性;

对于提取器的描述如下:新的提取器只要调用两个原来的提取器就行:

对于SHVZK,显然,存在模拟器,满足SHVZK的两个条件:1.可模拟 2.输出同分布

19.7.2 The OR-Proof construction
OR-Proof证明允许我们构造一个新的协议,该协议允许证明掌握两个声明的其中一个证据,不过这需要首先进行额外的假设:
假设一:所有组件协议可以使用同一个挑战空间;
假设二:所有组件协议都是SHVZK的;
因此,证明以下OR关系:

即为证明者可以向怀疑的验证者证明,自己掌握y0或者y1的证据,但是并不会打开其内容;
该协议运行如下:

其实办法很简单,只对一个协议进行真实的运行,对于另外一个协议只需要进行模拟的运行就行,因为我们已经在前文中假设了,这个两个协议都是SHVZK的。那么,对于验证者而言,其并不能看出是哪一个证据被掌握;
所以有如下的安全性定理:

其知识合理性和HVZK属性是显然的,这里不在做讨论。
19.8 Witness independence and applications
Sigma协议有一个非常有用的属性,被称为“witness independence”证据独立性;
也就是说,对于一个声明可能存在多个证据,一个不诚实的验证者不能指出一个诚实证明者用了哪一个证据,即为验证者只能知道证明的合法性,不能确定证明者P使用了哪一个证据与其进行交互。即使说,不诚实的验证者V有非常强的计算能力,能够计算出P与其交互的证据,然而,能力强大的不诚实验证者给出的证据也是和P的证据不相关的。这些都基于该声明存在多个证据与之对应的情景。
本节内容:
首先,给出具体细致的证据独立性定义。
其次,展示SHVZK实现了这个属性,并且即使是计算能力无界限的不诚实验证者,依然满足
最后,使用该属性构造抵抗积极敌手的ID认证协议;
19.8.1 Definition of witness independence
首先基于一个攻击游戏来定义证据独立性:

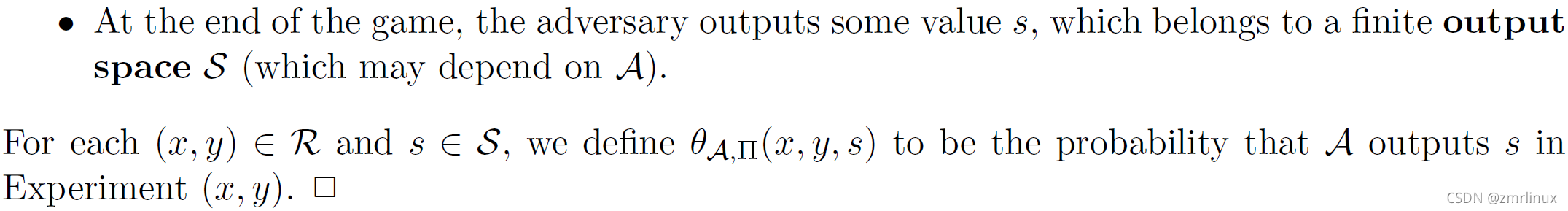
定义一个PV协议是sigma协议,并且存在关系R;给定一个敌手A,对于所有满足关系R的“声明-证据”对都分别存在一个这样的实验:
1. 初始化:敌手获得一个声明y
2. 敌手与多个P(x,y)实例进行交互,在每个实例实验中,挑战者扮演P的角色,给出诚实的输出,A扮演验证者的角色,对其进行验证(该验证者可能并不遵循V固有的验证算法)。并且,这些实验可能是并发的,敌手可能会依赖到协议运行为止之前的所有输入输出信息。
3.在攻击游戏结束时,敌手输出一些参数s, s 来源于一个有限的输出空间;
下面给出形式化定义:

这个概念是非常简单的,即为对应一个声明有多个证据,例如x 和 x`时,敌手对该声明实例输出的s, 在这两种情况下概率是相同的。这个定义捕获了一个非常强的情景,即为敌手的行为仅仅依赖于声明,不依赖于证明者使用的证据。在身份协议的分析中,有时使用该定义来应用于分析证据是独立的,例如,给出定义X 由G生成的私钥空间,Y由G生成的公钥空间,S由敌手生成的输出。则我们有以下等式:
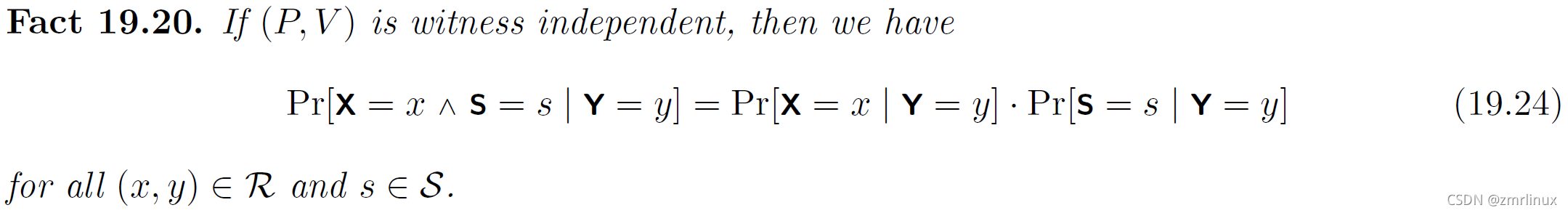
同样的也有以下的等价表达式:

19.8.2 Special HVZK implies witness independence
现在,我们给出SHVZK是实现了证据独立性的。

首先要给出一些辅助的定义:
使用coin定义证明者给出的承诺信息,则给出一个函数r来描述所有P的输出到所有P的输出的映射,那么,对于一个合法合理的PV交互(对于某一个C),有如下描述:
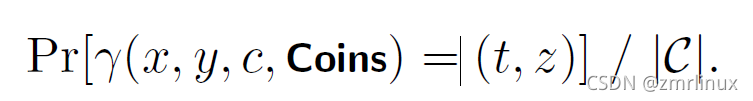
另外,给出一个模拟者Sim的映射函数为p,则模拟者Sim有如下的内容:
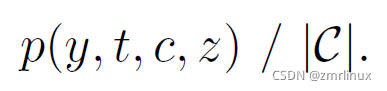
根据我们要证明的结果,这个两个概率是相等的,有如下表达式:
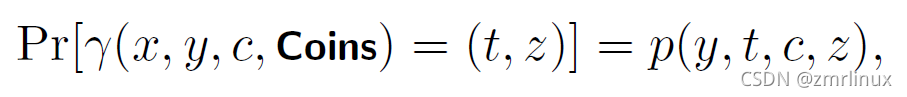
现在考虑,如果在攻击19.3中,如果敌手A能够与P的Q个拷贝进行交互,那么无论多少次模拟都应该和原始协议的映射输出s的概率相同,所以有:

进一步,定义Coins*为敌手选择的随机变量,则有:


19.8.3 Actively secure identification protocols
显然,满足SHVZK+ knowledge soundness的sigma协议构造的ID协议是可以抵抗窃听敌手,但是我们需要改协议能够抵抗积极敌手;
在身份协议中积极敌手意味着,该敌手可以扮演不诚实的验证者并发的与诚实证明者进行交互,回忆一下,窃听敌手只能安静的窃听诚实的PV之间进行交互的交易信息,而积极的敌手相当于可以参与到PV交互中。
给出通用构造如下:

安全定理如下:

证明过程,原书P765页,定理19.22. 此处不做进一步讨论。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








