吴恩达Coursera深度学习课程 course1-week3 浅层神经网络 总结

                                              P0前言

• 第一门课 : Neural Networks and Deep Learning (神经网络和深度学习)
• 第二周 : Shallow nerual networks (浅层神经网络)
• 主要知识点 : (nerual networks)神经网络、(Activation Functions)激活函数、(Gradient descent)梯度下降法、(Backpropagation)反向传播、(Random+Initialization)随机初始化等；

视频地址: https://mooc.study.163.com/learn/2001281002?tid=2001392029#/learn/announce

                                              P1总结

1.神经网络的表示

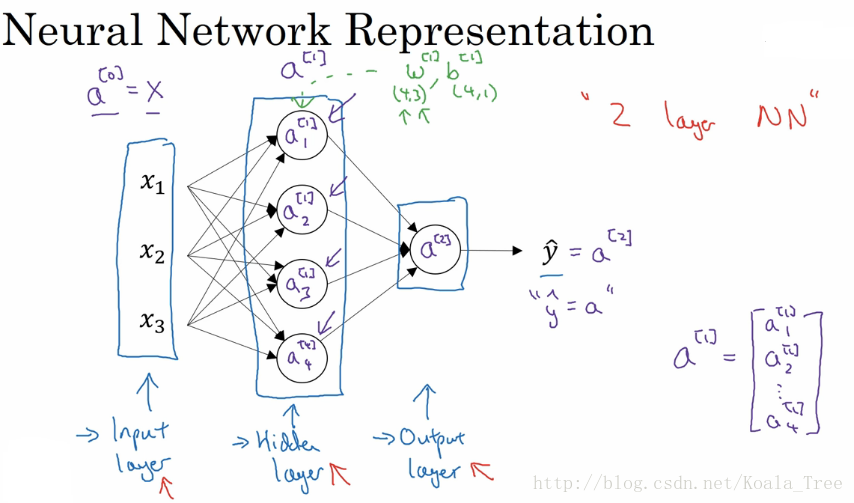
一个简单的两层神经网络(或者说三层: 输入层,隐藏层,输出层)的结构可以表示成:

1.1 神经元解释 (值的维度)

其中每个圈代表一个神经元,而一个神经元代表(能产生)一个1*M的向量(M表示样本个数)

一层神经元代表一个N*M的矩阵(N表示该层神经元个数)

如:  和两个神经元都是代表一个1*1的向量(这里样本只有一个x=[x1,x2,x3]T)

则是代表一个4*1的矩阵

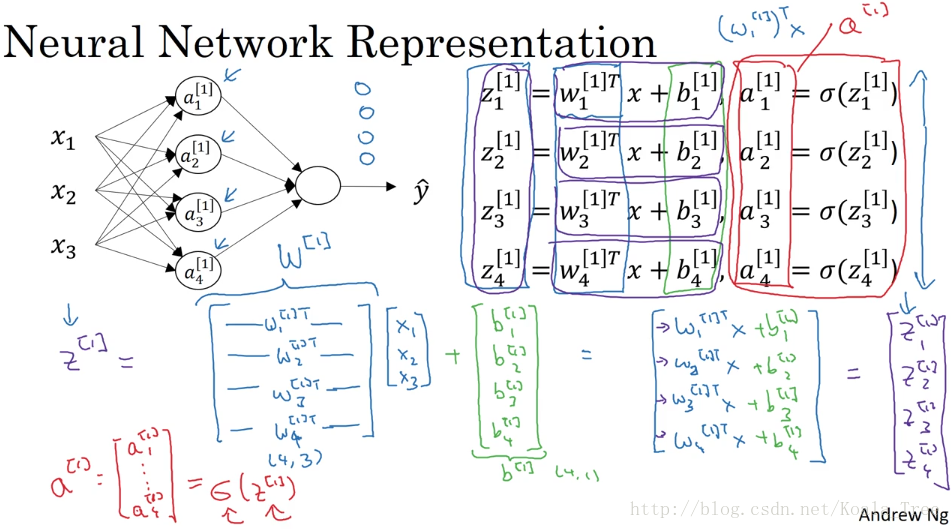
1.2 箭头解释 (参数的维度)

在神经网络中，我们以相邻两层为观测对象，前面一层作为输入，后面一层作为输出，两层之间的过渡过程(或者说计算过程)可以由箭头描述,  他可以表示两个参数矩阵和两种运算操作 :

参数矩阵:

• W = (,) 
• b = (,1)

运算操作:

• Z运算  (W.T*X+b)    # 在logistic regression中，一般我们都会用(,)来表示参数W大小所以有 转置 T
• A运算  sigmoid(Z)

以上图为例:

•  (4,3) 上图蓝色矩阵 ,   (4,1) 上图绿色矩阵
•  (1,4)  ,   (1,1)

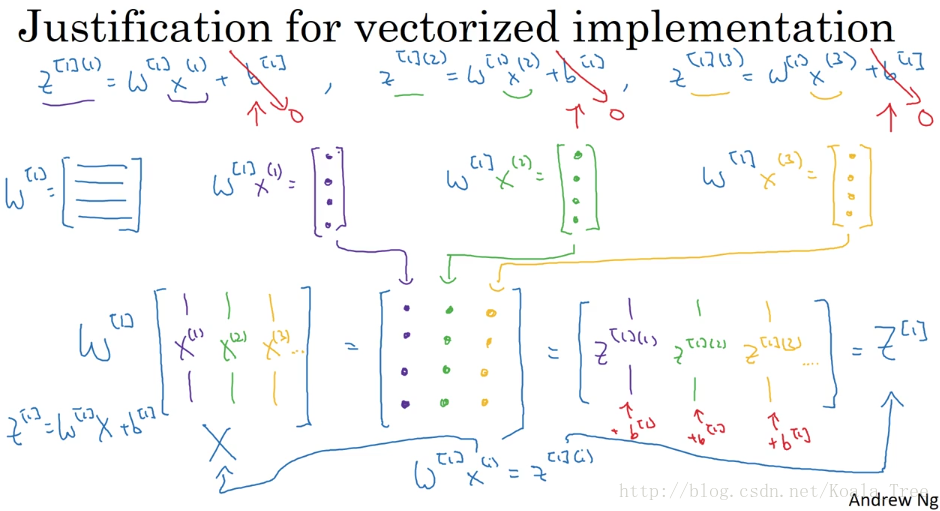
1.3 多个样本的向量化

如果有不止一个样本,参数W和b的维度不需要改变,因为由图可以看出，在m个训练样本中，每次计算都是在重复相同的过程，均得到同样大小和结构的输出,需要改变的是值的维度,包括X(这里可以视为A_0),Z_1,A_1,Z_2,A_2,维度计算参考1.1

这里需要补充说明X,我们把它视为A_0,他是(N,M)维的,这里N是一个样本的特征数(相当于每个特征都视为一个神经元)

#输入层和第一个隐藏层之间的箭头
Z_1 = W_1.T * X + b_1 #X视为A_0,这里*实际是dot操作,我简写了
A_1 = sigmoid(Z_1)

#第一隐层和输出层之间的箭头
Z_2 = W_2.T * A_1 + b_2
A_2 = sigmoid(Z_2)

1.3 总结

• 一个神经元视为一个向量   1*M   1*样本个数
• 一层神经元视为一个矩阵   N*M  神经元数*样本个数
• 箭头视为两个参数矩阵和两种运算操作  W,b,Z,A 

2 激活函数的选择

sigmoid和tanh的比较:

• 隐藏层：tanh函数的表现要好于sigmoid函数，因为tanh取值范围为[−1,+1]，输出分布在0值的附近，均值为0，从隐藏层到输出层数据起到了归一化（均值为0）的效果。
• 输出层：对于二分类任务的输出取值为{0,1}{0,1}，故一般会选择sigmoid函数。

sigmoid和tanh的共同缺点:

• sigmoid和tanh函数在当|z|很大(+z大或者-z小)的时候，梯度会很小，在依据梯度的算法中，更新在后期会变得很慢。在实际应用中，要使|z|尽可能的落在0值附近。

ReLU的优点:

• ReLU弥补了前两者的缺陷，当z>0时，梯度始终为1，从而提高神经网络基于梯度算法的运算速度。然而当z<0时，梯度一直为0，但是实际的运用中，该缺陷的影响不是很大。
• Leaky ReLU保证在z<0的时候，梯度仍然不为0。
• 在选择激活函数的时候，如果在不知道该选什么的时候就选择ReLU，当然也没有固定答案，要依据实际问题在交叉验证集合中进行验证分析。

3.神经网络中的梯度下降

以上图三层神经网络为例可得如下代码,求导的详细推导过程见我的另一篇博客:https://blog.csdn.net/zongza/article/details/82932325

#正向传播

Z_1 = np.dot(W_1.T,X) + b_1    # 维度N1*M ,N1表示第一隐层的神经元数
A_1 = sigmoid(Z_1)             # 维度N1*M

Z_2 = np.dot(W_2.T,A_1) + b_2  # 维度N2*M ,N2表示输出层的神经元数
A_2 = sigmoid(Z_2)             # 维度N2*M

L = cross_entropy(A_2,Y)       # 标量(具体实现待研究)

#反向传播

dZ_2 = A_2 - Y                                    # 维度N2*M ,N2表示输出层的神经元数
dW_2 = 1/m* np.dot(dZ_2, A_1.T)                   # 维度N2*N1 
db_2 = 1/m* np.sum(dZ_2,axis = 1,keepdims = true) # 维度N2*1

dZ_1 = np.dot(W_2,dZ_2) * A_1*(1-A_1)           # 维度N1*M
dW_1 = 1/m* np.dot(dZ_1, X.T)                     # 维度N1*N0,N0表示单样本的特征数
db_1 = 1/m* np.sum(dZ_1,axis = 1,keepdims = true) # 维度N1*1

4.随机初始化

如果在初始时，两个隐藏神经元的参数设置为相同的大小，那么两个隐藏神经元对输出单元的影响也是相同的，通过反向梯度下降去进行计算的时候，会得到同样的梯度大小，所以在经过多次迭代后，两个隐藏层单位仍然是对称的。无论设置多少个隐藏单元，其最终的影响都是相同的，那么多个隐藏神经元就没有了意义。

初始化tips:

• W参数必须要进行随机初始化
• b参数不存在对称性问题,可以设置为0

以上图三层神经网络为例:

#输入层和第一隐层之间的箭头
W_1 = np.random.randn(4,3)*0.01  #rand() 01分布 randn() 标准正太分布
b_1 = np.zeros((4,1))

#第一隐层和输出层之间
W_2 = np.random.randn(1,4)*0.01
b_2 = np.zeros((1,1))

这里我们将W的值乘以0.01是为了尽可能使得权重W初始化为较小的值，这是因为如果使用sigmoid函数或者tanh函数作为激活函数时，W比较小则Z=WX+b所得的值也比较小，处在0的附近，0点区域的附近梯度较大，能够大大提高算法的更新速度。而如果W设置的太大的话，得到的梯度较小，训练过程因此会变得很慢。

ReLU和Leaky ReLU作为激活函数时，不存在这种问题，因为在大于0的时候，梯度均为1。