hdoj1715-大菲波数

题目链接

Problem Description

Fibonacci数列，定义如下：
f(1)=f(2)=1
f(n)=f(n-1)+f(n-2) n>=3。
计算第n项Fibonacci数值。

Input

输入第一行为一个整数N，接下来N行为整数Pi（1<=Pi<=1000）。

Output

输出为N行，每行为对应的f(Pi)。

Sample Input

5
1
2
3
4
5

Sample Output

1
1
2
3
5

思路

此题就是大数的运算，我设置了一个二维数组来储存结果，为了减少运算次数，我每次将四位放在一起进行运算；如下图：

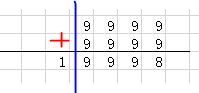
上面是9999+9999的运算，因为个数组元素储存的四位数，当出现上述结果时就得进“1”，也就是将比当前运算的位数的更高一位加一；因为我是用的int数组，int类型的最大取值为5位数，因此我们每次只能进行四位数的运算，否则会出现溢出，如果想每次计算更多位，可以采用long long型数组储存结果；

code

#include <iostream>
#include <iomanip>
#include <cstring>

using namespace std;

const int B = 10000;
const int M = 1000+5;

int fi[M][60];

void add(int n)
{
    int loc = 0;
    while(fi[n-1][loc] != 0 || fi[n-2][loc] != 0)
    {
        int temp = fi[n-1][loc] + fi[n-2][loc];
        if(temp >= B)
        {
            fi[n][loc] += temp % B;
            fi[n][loc+1] += 1;
        }
        else
        {
            fi[n][loc] += temp;
        }
        loc ++;
    }
}

int main()
{
    memset(fi, 0, sizeof(fi));
    fi[1][0] = fi[2][0] = 1;
    for(int i = 3; i < M; i ++)
    {
        add(i);
    }
    int n;
    cin >> n;
    while(n --)
    {
        int p;
        cin >> p;
        int loc = 59;
        while(fi[p][loc] == 0)
        {
            loc --; //找出最高位
        }
        cout << fi[p][loc];
        for(int i = loc-1; i >= 0; i --)
        {
            cout << setw(4) <<setfill('0') << fi[p][i];
        }
        cout << endl;
    }
    return 0;
}