洛谷 P1192 台阶问题 动态规划 和记忆化搜索

题目：

https://www.luogu.com.cn/problem/P1192

记忆化搜索是可以转化成动态规划的，它们的状态变化的方程是一样。画的树图是一样的。        案例N = 5，K = 2.

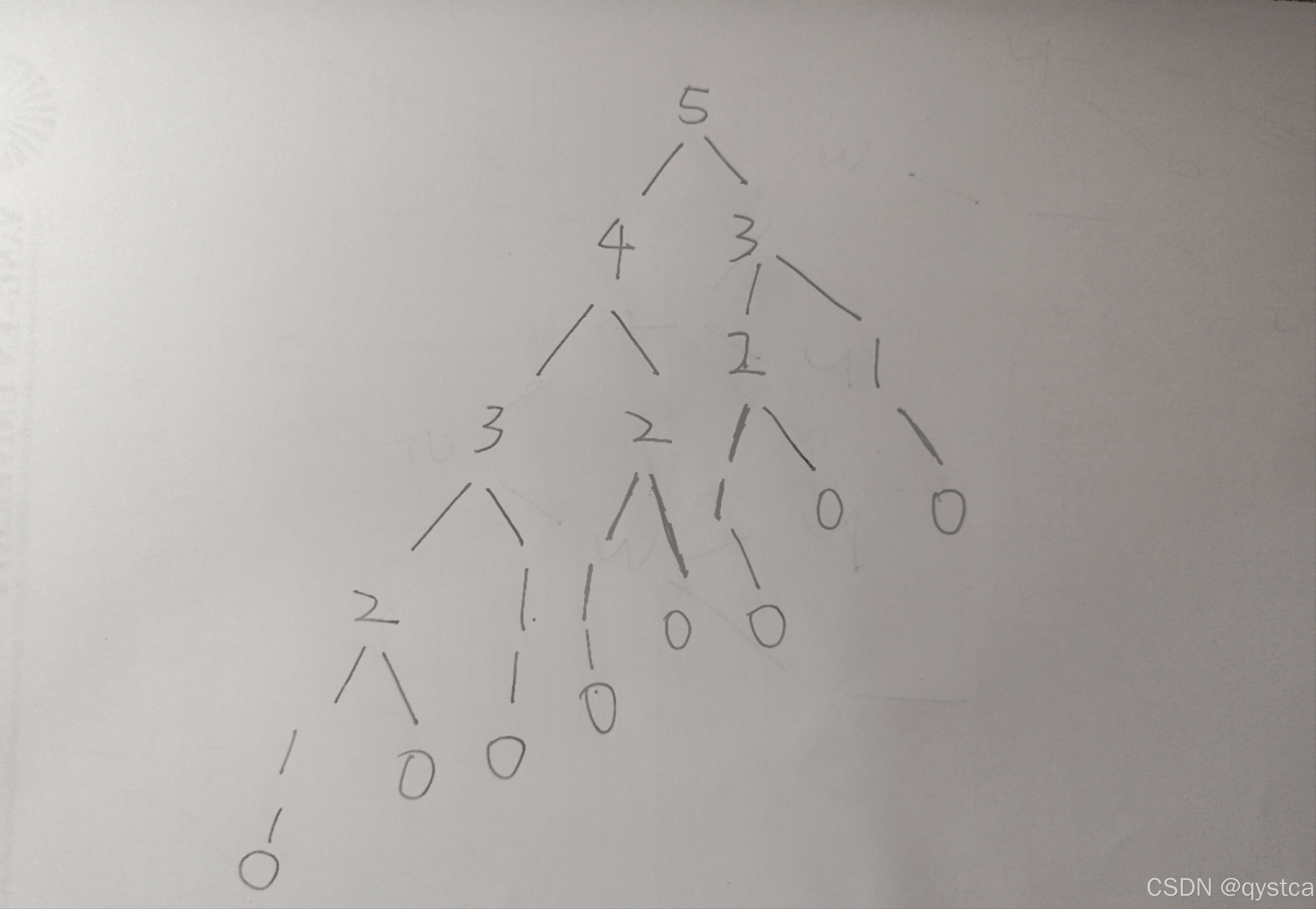
dfs（x-1）+ dfs (x-2) : dp[i-1] + dp[i-2] = 1 : 1;这两个方程是1比1关系。

记忆化搜索是先递后归，在这张图中递是从5开始从第一个子树开始向下寻找答案，不断分解子问题。归就是从底端回溯，收集答案的过程。并储存搜索过的点，再下一个子树的时候就减少很多时间。num[0] 的值是在递归调用 dfs(0) 时隐式地设置为 1 的。这个设置是基于递归基准情况和记忆化技术的正确应用。

代码如下

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;

int n, k;
const int mod = 100003;
const int maxn = 1e5 + 5;
LL num[maxn];

LL dfs(int x)
{
    if(x < 0)//x < k的时候不存在直接返回0，所以最大也只会写到dfs(1~x)的范围 
	return 0;
	
    else if(num[x])
	return num[x];
	
    else if(x == 0)
	return num[x] = 1;

    LL ans = 0;
    for(int i = 1; i <= k; i++)
	{
        ans = (ans + dfs(x - i)) % mod;//当x > k其实就是 dfs(x-k ~ x-1), 当x = k时就是dfs(1~x),当x < k的时候，调用下一个dfs函数的时候直接返回0
    }
    num[x] = ans; //记忆 
    return num[x];
}

int main()
{
	cin >> n >> k;
	cout << dfs(n);
    return 0;
}

动态规划是一样的，但是是凑出方案数的，就像从树底部向上爬，一步一步凑出来，而记忆化搜索是分解子问题，从上往下，归的时候发方向也是从下往上。

代码如下：

#include <iostream>
#include <vector>
const int MAX = 1e5 + 5;
const int MOD = 100003;
using namespace std;

int main()
 {
    int n, k;
    cin >> n >> k;

    int dp[MAX] = {0};
    dp[0] = 1;//可能有人会写dp[1] = 1;也可以把i改成2开始就可以。

    for (int i = 1; i <= n; ++i)
     {
        for (int j = 1; j <= k && j <= i; ++j) 
        {
            dp[i] = (dp[i] + dp[i - j]) % MOD;
        }
    }

    cout << dp[n] << endl;
    return 0;
}

它们的结果图都是AC