数据结构—线性结构—线性及其实现

2.1线性及其实现

一、如何表示多项式

方法1：顺序存储结构直接表示

这个方法用了一个数组，把数组的对应系数存了起来。这个方法的优点是：多项式相加比较好算，缺点是：下面要表示2000次的时候，要一个2001大的数组，显然是巨大的浪费。

方法2：顺序存储结构表示非零项

特点，只表示非零向量。每个非零向量有两个信息，系数和指数，所以可以将一个多项式看成是一个（ai, i ）二元组的集合。
用结构数组表示：数组分量有系数、指数组成的结构。对应一个非零项。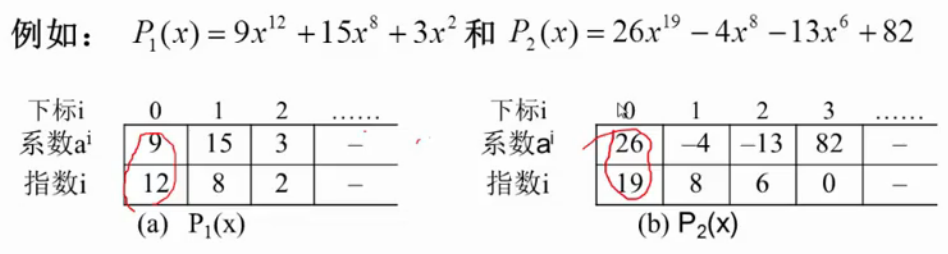
这样表示运算方便吗？要有序进行存储。
两个多项式相加。也不一定要用数组来做，也可以用链表

方法三：链表结构存存储非零项

链表中每个结点存储多项式中的一个非零项，包含洗漱和指数两个数据域以及一个指针域。

typedef struct PulyNode *Polynomial;
typedef struct PolyNode{
    int coef;
    int expon;
    Polynomial link;
}

存储的形式为
存储方法，要么数组，要么链表

什么是线性表？

定义：有同类型数据元素构成有序序列的线性结构。
- 表中元素个数成为线性表的长度。
- 线性表没有元素时，称为空表。
- 表起初位置成为表头，表结尾称为表尾。

线性表的抽象数据类型

线性表的存储方法：线性表的顺序存储实现
利用数组的连续存储空间顺序存放