接上一节 第二章-信源与信息熵(一)
2.3 离散序列信源的熵
简介
1. 离散无记忆序列信源
a) 离散无记忆信源的序列熵
b) 离散无记忆信源的符号熵
2. 离散有记忆序列信源
a) 平稳信源
i. 序列熵
ii. 符号熵
b) 马尔可夫信源
i. 序列熵
ii. 符号熵
3. 从最简单的离散无记忆序列→平稳序列→马氏序列
4. 无记忆
a) 简单
5. 有记忆
a) 无限记忆
b) 有限记忆
i. 马尔可夫信源
1. 广泛出现在计算机、通讯、自动控制、随机服务、可靠性、生物学、经济、管理、教育、气象、物理、化学等众多领域
2. Markov Process 的最简单的两种类型
a) 离散时间离散状态Markov链:本书
b) 连续时间离散状态Markov链
一.离散无记忆序列信源的熵
序列熵
平均每个符号熵(消息熵)
离散无记忆序列符号熵 = 序列熵的算术平均值
二.离散有记忆序列信源的熵
离散有记忆信源的序列熵和消息熵
先考虑平稳序列
三.平稳信源
定义:若信源产生的随机序列
满足
a) 所有Xi都取值于有限的信源符号集A=(a1,a2,…,aq)
b) A中每个状态是离散的、状态明晰的
c) 随机序列是平稳的,即对所有非负整数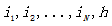
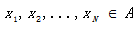
平稳信源发出的符号序列的概率分布与时间起点无关
平稳信源发出的符号序列的概率分布函数可以在时间轴上平移
讨论N长的时间序列时不需要考虑时间起点
联合概率与事件的起点没有关系
下面来看看平稳的定义。
一维平稳信源
随机变量序列 X=X1X2…XN,若任意两个不同时刻i和j信源发出消息的概率分布完全相同,即
一维平稳信源无论在什么时刻均以 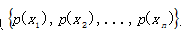
一维平稳信源即无记忆信源。
二维平稳信源
对于一个一维平稳信源,如果联合概率分布 P(XiXi+1)也与时间起点无关,即
i,j为任意整数,且i≠j。
二维平稳信源在任何时刻发出两个符号的概率完全相同
二维平稳信源的二维联合分布P(X1X2)与时间起点无关
离散平稳信源
如果各维联合概率分布均与时间起点无关,即对两个不同的时刻i和j,有
这种各维联合概率均与时间起点无关的完全平稳信源称为离散平稳信源。
离散平稳信源一般是有记忆信源
发出的各个符号之间具有统计关联关系。
统计关联性可用两种方式表示:
联合概率
用信源发出的一个符号序列的整体概率,即N个符号的联合概率来反映有记忆信源的特征,这种信源是发出符号序列的有记忆信源;
条件概率
用信源发出符号序列中各个符号之间的条件概率来反映记忆特征,这是发出符号序列的马尔可夫信源
用条件概率更符合我们的观察习惯。
a) 序列熵H(XN)
b) 符号熵
c) 极限熵
d) 极限熵的意义
1. 多符号离散平稳信源实际上就是信源在不断地发出符号,符号之间的统计关联关系也并不仅限于长度N,而是伸向无穷远。
2. 研究实际信源,必须求出信源的极限熵H∞
离散平稳信源序列熵的特点
- HL(X) ≥ H(XL/XL-1)
- H(XL/XL-1)是L的单调非增函数。
- HL(X)是L的单调非增函数
- 极限熵H∞
H∞是否存在?
H∞是存在的,且等于关联长度N趋于无穷时,条件熵的极限值。
极限熵存在定理(夹逼证明)
对任意离散平稳信源,若H1(X)< ∞,则有
如何计算H∞?
通过极限熵的存在性定理,可证明H(XN/XN-1)的值在HN(X)和HN+j(X)之间
令N->∞,有HN(X) ->∞和HN+j(X) ->∞,则
四.马尔可夫信源
当信源的记忆长度为m+1时,该时该发出的符号与前m个符号有关联性,而与更前面的符号无关。
由于高阶马尔可夫信源需要引入矢量进行分析,现方法将矢量转化为状态变量。定义状态:
信源在某一时刻出现符号概率xj与信源此时所处状态si有关,用条件概率表示p(xj/si),状态转移概率表示为p(sj/si)
设系统现在时刻的状态Si,
Sj与过去时刻的状态无关,仅与现在时刻的状态Si有关。
系统的将来与过去无关:马尔可夫特性,即“无后效性”
状态转移概率
为知道系统状态的转化情况,采用状态转移概率,时刻m系统处于状态Si,经过n-m步后转移至状态Sj的概率
一步、k步状态转移概率
特别关心n-m=1情况,pij(m,m+1)
一步转移矩阵
齐次马尔科夫链
定义:如果从状态i转移到状态j的概率与m无关,则称这类MovKov链为齐次(homogeneous),即
对于齐次马尔可夫链,一步转移概率完全决定了k步转移概率
切-柯方程
对于具有k步转移概率的齐次马尔可夫链,存在k步转移概率pij(k)与l步和k-l步转移概率之间的切普曼-柯尔莫郭洛夫方程:
值得注意的是:转移概率pij不包括初始分布,即第0次随机实验中X0=Si的概率不能有转移概率pij表达。
Markov链的遍历性
定义:若齐次马尔可夫链对一切状态Si,Sj存在不依赖于i的参数Pj,使得 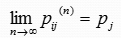
则称其具有遍历性,pj称为平稳分布 。
Pj也记为Wj
遍历性的意义:
不论质点从哪个状态出发,当转移步数n充分大时,转移到状态Sj的概率 都近似等于某个常数pj。
即如果转移步数n充分大,就可以用常数pj作为n步转移概率的近似值
遍历性的条件
两个条件:
不可约性,对于任意一对I和j, 都存在至少一个k,使pij(k)>0.
非周期性,所有pij(n)>0的n中没有比1大的公因子。
定理
设P是某一马尔可夫链的状态转移矩阵,则该稳态分布存在的充要条件是存在一个正整数N,使矩阵PN中的所有元素均大于零。
马尔可夫链的稳态分布
如果马尔可夫链具有遍历性,意味着马尔可夫信源在初始时刻可以处在任意状态,然后信源状态之间可以转移。
由初始分布及各时刻的一步转移概率就可以完整描述马尔可夫链的统计特性。足够长时间之后,信源处于什么状态已与初始状态无关,每种状态出现的概率已达到一种稳定分布,即平稳分布.
对于有限状态马尔可夫链,如果存在一个数集W1,W2,…,Wr,且满足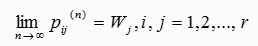
则称该马尔可夫链的稳态分布存在。
t=n-1与t=n时刻的状态方程
设
则有 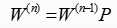
t=n时刻的状态分布矢量是初始分布矢量与转移矩阵P的n次幂的乘积
五.稳态分布存在性定理
1. 设有一马尔可夫链,其状态转移矩阵为P,其稳态分布为Wj,则有
W=(W1,W2,…,Wr)是该链的稳态分布矢量,即
WP=W
如果初始分布W(0)=W,则对所有的n,W(n)=W;
W是该链的唯一稳态分布
2. 设P为某一马尔可夫链的状态转移矩阵,则该链稳态分布存在的充要条件是存在一个正整数N,使矩阵PN中的所有元素均大于零。
从该定理可以推论出,如果P中没有零元素,即任一状态经一步转移之后便可以到达其他状态,即稳态分布存在。
六.马尔可夫信源与马尔可夫链
一般的m阶马尔可夫信源 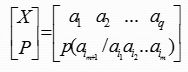
其状态转移概率p(Sj/Si)由信源符号条件概率确定
七.m阶马尔可夫信源的极限熵
当时间足够长时,遍历的m阶马尔可夫信源可视为平稳信源
又因为信源发出的符号只与最近的m个符号有关
由前面的极限熵定理:
对任意离散平稳信源,若H1(X)<∞
可得
即m阶马尔可夫信源的极限熵等于m阶条件熵。









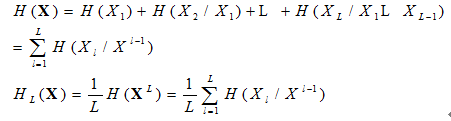
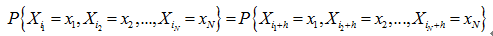
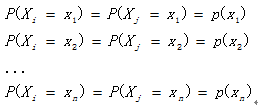
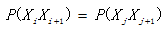
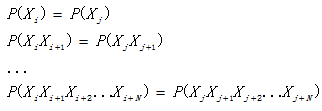
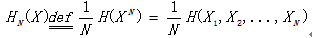
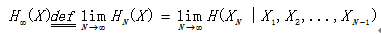
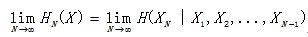
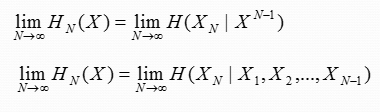
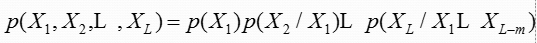
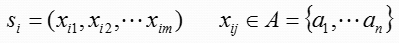
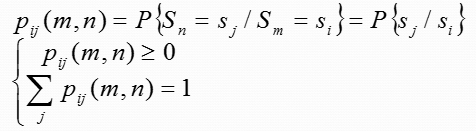
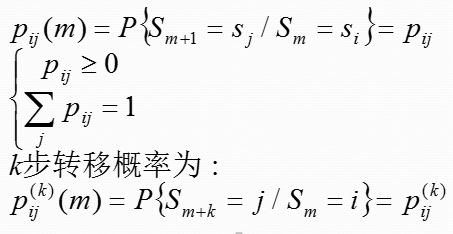
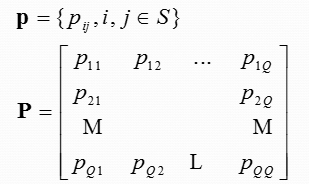
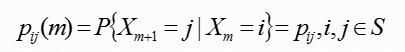
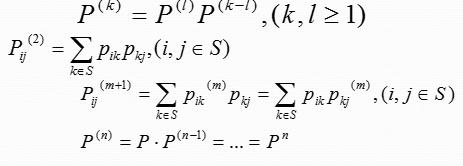
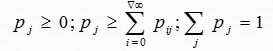
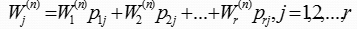
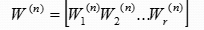
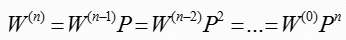
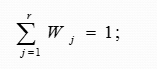
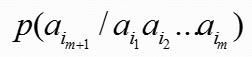
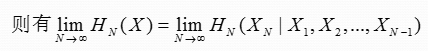
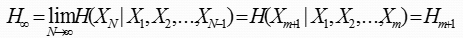
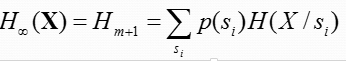














 4792
4792











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








