最小二乘法及其应用

1 实验目的

1. 了解最小二乘法的基本原理；
2. 了解超定方程组的最小二乘解法；
3. 使用最小二乘法解决实际问题；

2 实验内容

由化学实验得到某物质浓度与时间的关系如下：

求浓度与时间的二次拟合函数。

求解浓度与时间的二次拟合函数是关于3个参数的最小二乘问题，可采用的方法有QR分解法、SVD分解法和正规方程法。在本实验中，正规方程被用来求解浓度与时间的最小二乘问题。其中正规方程为

$$\theta = (X^TX)^{-1}X^Ty$$
其中 $\theta$ 为参数，即二次函数的系数， $X$ 为数据矩阵，即时间 $t$ 对应的二次函数所构建的数据矩阵， $y$ 为浓度向量。

3 实验程序

正规方程函数如下所示：

function [theta, Y] = normalEq(t, y)
%正规方程求最小二乘解
% 输入: t = 时间向量
%       y = 浓度向量
% 输出：theta = 第 0 次 to 第 n 的多项式系数
%       Y = theta 系数下 t 对于的浓度值

X = [ones(size(t)) t t.^2];     % [0 1 2] 次
theta = pinv(X'*X)*X'*y;        % 正规方程
Y = X*theta;                    % 拟合的浓度值

实验主函数如下所示：

function main4()
%实验四的主函数

t = 1:16;
y = [4 6.4 8 8.8 9.22 9.50 9.70 9.86 10 10.2 ... 10.32 10.42 10.50 10.55 10.58 10.60];
theta = normalEq(t', y');
t1 = linspace(1, 16, 50);
y1 = polyval(theta(length(theta) : -1 : 1), t1);
%% 作图
plot(t1, y1)
hold on
plot(t, y, 'ro')
hold on
xlabel('时间 (t)');
ylabel('浓度')
hold off

4 实验结果分析

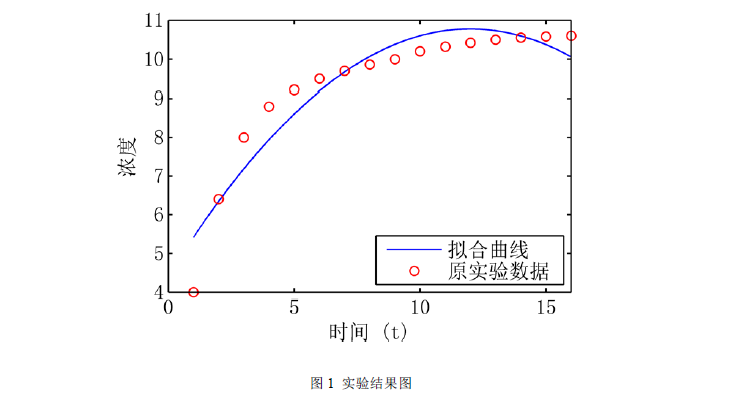
最小二乘结果的误差为 $2.2152$。

5 实验结论

针对最小二乘问题，正规方程提供了一种有效的求解方法。
通过正规方程我们拟合得到了二次函数，但显然二次函数对实验数据的拟合效果并不是很好，尤其是在随时间增大时，浓度值明显趋向饱和，而二次函数趋向降低，因此对该问题有必要选择对数函数 $y=a+b \ln x$ 作为拟合的猜想。