上次看的那个视频讲线段树的时候压根没讲懒标记,然后我今天去写题目直接被薄纱!都是70分,剩下3个节点tml!!!
懒标记
我们在修改一些区间的时候,按照我昨天来学的来修改要改到最下面的叶节点去,可是这样子就没有了线段树的精华的区间修改,这样子我们时间复杂度会大大增加就像这样子
void updata(int arr[], int tree[], int node, int start, int end, int idx, int val)//位置 改变后的数
{
if (start == end)
{
arr[idx] = val;
tree[node] = val;
}
else
{
int mid = (start + end) / 2;
int left_node = node * 2 + 1;
int right_node = node * 2 + 2;
if (idx >= start && idx <= mid)
{
updata(arr, tree, left_node, start, mid, idx, val);
}
else
{
updata(arr, tree, right_node, mid+1, end, idx, val);
}
tree[node] = tree[left_node] + tree[right_node];
}
}于是我们就引入了懒标记这个东西,简单的来说,就是我们如果是要修改6到9,那么我们可以直接在6到9这个地方加上一个lazy=我们要增加的值,然后我们如果在后面要运用这个节点下面的节点的时候,就把这个lazy下放,这样子我们就可以不需要一定要找到最下面的节点,大大节约了时间复杂度!

然后就是我写的线段树的题目,不过只有70分(;´༎ຶД༎ຶ`)
# 【模板】线段树 1
## 题目描述
如题,已知一个数列,你需要进行下面两种操作:
1. 将某区间每一个数加上 $k$。
2. 求出某区间每一个数的和。
## 输入格式
第一行包含两个整数 $n, m$,分别表示该数列数字的个数和操作的总个数。
第二行包含 $n$ 个用空格分隔的整数,其中第 $i$ 个数字表示数列第 $i$ 项的初始值。
接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数,表示一个操作,具体如下:
1. `1 x y k`:将区间 $[x, y]$ 内每个数加上 $k$。
2. `2 x y`:输出区间 $[x, y]$ 内每个数的和。
## 输出格式
输出包含若干行整数,即为所有操作 2 的结果。
## 样例 #1
### 样例输入 #1
```
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
```
### 样例输出 #1
```
11
8
20
```
## 提示
对于 $30\%$ 的数据:$n \le 8$,$m \le 10$。
对于 $70\%$ 的数据:$n \le {10}^3$,$m \le {10}^4$。
对于 $100\%$ 的数据:$1 \le n, m \le {10}^5$。
保证任意时刻数列中所有元素的绝对值之和 $\le {10}^{18}$。
**【样例解释】**

#include <stdio.h>
void bulid_tree(long long arr[], long long tree[], int node, int start, int end)
{
if (start == end)
{
tree[node] = arr[start];
}
else
{
int mid = (start + end) / 2;
int left_node = node * 2;
int right_node = node * 2+1;
bulid_tree(arr, tree, left_node, start, mid);
bulid_tree(arr, tree, right_node, mid+1, end);
tree[node] = tree[left_node] + tree[right_node];
}
}
long long qureytree(long long arr[], long long tree[], int node, int start, int end, int L, int R)
{
if (R<start||L>end)
{
return 0;
}
if (L <= start && R >= end)
{
return tree[node];
}
else
{
int mid = (start + end) / 2;
int left_node = node * 2;
int right_node = node * 2 + 1;
long long sum_left = qureytree(arr, tree, left_node, start, mid, L, R);
long long sum_right= qureytree(arr, tree, right_node, mid+1, end, L, R);
return sum_left + sum_right;
}
}
void up_data(long long arr[], long long tree[], int node, int start, int end, int idx, int val)
{
if (start==end)
{
arr[start] = arr[start] + val;
tree[node] = tree[node] + val;
}
else
{
int mid = (start + end) / 2;
int left_node = node * 2;
int right_node = node * 2 + 1;
if (idx >= start && idx <= mid)
{
up_data(arr, tree, left_node, start, mid, idx, val);
}
else
{
up_data(arr, tree, right_node, mid + 1, end, idx, val);
}
tree[node] = tree[left_node] + tree[right_node];
}
}
int main()
{
long long arr[1000001], tree[1000001];
int n, m,i;
int x, y, k, xx;
//printf("8888");
scanf("%d%d", &n, &m);
for (i = 1; i <= n; i++)
{
scanf("%lld", &arr[i]);
}
bulid_tree(arr, tree, 1, 1, n);
//printf("%d")
while (m--)
{
scanf("%d", &xx);
if (xx == 1)
{
scanf("%d%d%d", &x, &y, &k);//将区间 [x, y]内每个数加上 k。
for (i = x; i <= y; i++)
{
up_data(arr, tree, 1, 1, n, i, k);
}
}
if (xx == 2)
{
//printf("*****");
scanf("%d%d", &x, &y);//输出区间 [x, y]内每个数的和。
printf("%lld\n", qureytree(arr, tree, 1, 1, n, x, y));
}
}
}# 【模板】线段树 2
## 题目描述
如题,已知一个数列,你需要进行下面三种操作:
- 将某区间每一个数乘上 $x$
- 将某区间每一个数加上 $x$
- 求出某区间每一个数的和
## 输入格式
第一行包含三个整数 $n,m,p$,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 $n$ 个用空格分隔的整数,其中第 $i$ 个数字表示数列第 $i$ 项的初始值。
接下来 $m$ 行每行包含若干个整数,表示一个操作,具体如下:
操作 $1$: 格式:`1 x y k` 含义:将区间 $[x,y]$ 内每个数乘上 $k$
操作 $2$: 格式:`2 x y k` 含义:将区间 $[x,y]$ 内每个数加上 $k$
操作 $3$: 格式:`3 x y` 含义:输出区间 $[x,y]$ 内每个数的和对 $p$ 取模所得的结果
## 输出格式
输出包含若干行整数,即为所有操作 $3$ 的结果。
## 样例 #1
### 样例输入 #1
```
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
```
### 样例输出 #1
```
17
2
```
## 提示
【数据范围】
对于 $30\%$ 的数据:$n \le 8$,$m \le 10$
对于 $70\%$ 的数据:$n \le 10^3 $,$ m \le 10^4$
对于 $100\%$ 的数据:$ n \le 10^5$,$ m \le 10^5$
除样例外,$p = 571373$
(数据已经过加强^\_^)
样例说明:
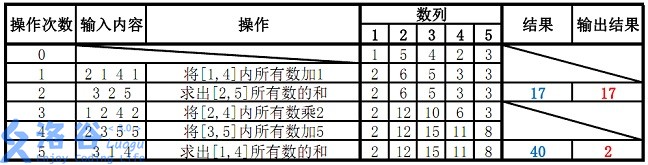
故输出应为 $17$、$2$( $40 \bmod 38 = 2$ )
#include <stdio.h>
void bulid_tree(long long arr[], long long tree[], int node, int start, int end)
{
if (start == end)
{
tree[node] = arr[start];
}
else
{
int mid = (start + end) / 2;
int left_node = node * 2;
int right_node = node * 2 + 1;
bulid_tree(arr, tree, left_node, start, mid);
bulid_tree(arr, tree, right_node, mid + 1, end);
tree[node] = tree[left_node] + tree[right_node];
}
}
long long qureytree(long long arr[], long long tree[], int node, int start, int end, int L, int R)
{
if (R<start || L>end)
{
return 0;
}
if (L <= start && R >= end)
{
return tree[node];
}
else
{
int mid = (start + end) / 2;
int left_node = node * 2;
int right_node = node * 2 + 1;
long long sum_left = qureytree(arr, tree, left_node, start, mid, L, R);
long long sum_right = qureytree(arr, tree, right_node, mid + 1, end, L, R);
return sum_left + sum_right;
}
}
void up_data(long long arr[], long long tree[], int node, int start, int end, int idx, int val)
{
if (start == end)
{
arr[start] = arr[start] + val;
tree[node] = tree[node] + val;
}
else
{
int mid = (start + end) / 2;
int left_node = node * 2;
int right_node = node * 2 + 1;
if (idx >= start && idx <= mid)
{
up_data(arr, tree, left_node, start, mid, idx, val);
}
else
{
up_data(arr, tree, right_node, mid + 1, end, idx, val);
}
tree[node] = tree[left_node] + tree[right_node];
}
}
void up_data1(long long arr[], long long tree[], int node, int start, int end, int idx, int val)
{
if (start == end)
{
arr[start] = arr[start]*val;
tree[node] = tree[node]*val;
//printf("%d\n", tree[node]);
}
else
{
int mid = (start + end) / 2;
int left_node = node * 2;
int right_node = node * 2 + 1;
if (idx >= start && idx <= mid)
{
up_data1(arr, tree, left_node, start, mid, idx, val);
}
else
{
up_data1(arr, tree, right_node, mid + 1, end, idx, val);
}
tree[node] = tree[left_node] + tree[right_node];
}
}
int main()
{
long long arr[1000000], tree[1000000],k;
int n, m, i,p;
int x, y, xx;
//printf("8888");
scanf("%d%d%d", &n, &m,&p);
for (i = 1; i <= n; i++)
{
scanf("%lld", &arr[i]);
}
bulid_tree(arr, tree, 1, 1, n);
//printf("%d")
while (m--)
{
scanf("%d", &xx);
if (xx == 1)
{
scanf("%d%d%lld", &x, &y, &k);
for (i = x; i <= y; i++)
{
up_data1(arr, tree, 1, 1, n, i, k);
}
}
if (xx == 2)
{
scanf("%d%d%lld", &x, &y, &k);//将区间 [x, y]内每个数加上 k。
for (i = x; i <= y; i++)
{
up_data(arr, tree, 1, 1, n, i, k);
}
}
if (xx == 3)
{
//printf("*****");
scanf("%d%d", &x, &y);//输出区间 [x, y]内每个数的和。
printf("%lld\n", qureytree(arr, tree, 1, 1, n, x, y)%p);
}
}
}等我明天把懒标记的代码搞出来!!!拿下这两个题目!!!






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








