一、什么是线性代数?
通俗解析
线性代数 是一门研究 向量、矩阵、线性方程组 及它们之间关系的数学分支。我们可以通过以下方式直观理解它:
🌟 核心概念:三块积木
-
向量(Vector)
→ 如:物理中的力、速度(有方向和大小的箭头)
→ 用途:表示数据组(如房价= [面积, 楼层, 地段]) -
矩阵(Matrix)
→ 如:Excel表格的数字阵列
→ 用途:批量处理方程(同时解多个线性方程) -
张量(Tensor)
→ 进阶版矩阵(立方体数据堆,如一张RGB图片=宽×高×3颜色通道)
🎯 四大主力应用
❶ 解线性方程组
▸ 生活场景:配制药剂需要混合不同浓度溶液
▸ 数学表达:
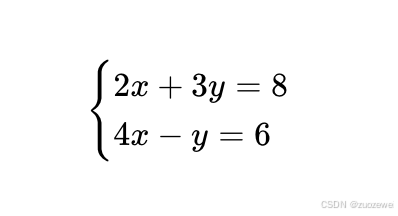
→ 矩阵解法:用 增广矩阵 快速求出药品配比
❷ 空间变换(线性变换)
▸ 生活场景:手机屏幕旋转图片
▸ 操作工具:

→ 输入原始坐标→矩阵乘法→输出旋转后坐标
❸ 降维与特征提取
▸ 应用案例:人脸识别中的主成分分析(PCA)
▸ 关键步骤:
- 计算协方差矩阵 → 找主要变化方向(特征向量) → 保留关键特征降低数据维度
❹ 机器学习基石
▸ 神经网络:权重更新 = 矩阵乘法
▸ 推荐系统:用户-商品评分矩阵分解(奇异值分解SVD)
📚 知识地图(从基础到高端)
| 层级 | 重点内容 | 典型问题 |
|---|---|---|
| 青铜 | 向量加减法、点积 | 两力合成后的方向 |
| 白银 | 矩阵乘法、行列式 | 判断方程组是否有解 |
| 黄金 | 特征值分解 | 预测系统长期状态(如人口增长模型) |
| 王者 | 奇异值分解(SVD) | 图像压缩(保留95%信息量,大小缩小10倍) |
💡 记住三个核心思想
- 线性组合:任何复杂操作都能拆解为“加法”和“数乘”(如:用RGB三原色混合出任何颜色)
- 矩阵=函数:矩阵乘法本质是对数据的变换(旋转、缩放、剪切)
- 降维打击:高维数据通过线性代数工具能找到简洁的本质特征(如:用3个主成分代替100个原始指标)
🛠️ 图示:矩阵变换对图片的影响

解读:
- 黄色方块 → 原图
- 红色菱形 → 应用旋转矩阵(45度)
- 蓝色扁矩形 → 应用缩放矩阵(x方向1.5倍,y方向0.7倍)
- 绿色平行四边形 → 应用剪切矩阵(侧边倾斜)
❓ 当你遇到线性代数时,可以问
- 这个问题是否能用 向量/矩阵 更简洁地表达?
- 这些数据之间是否存在 线性关系 (比如成比例?)
- 是否需要对数据进行 降维 或 特征提取?
通过这种思维方式,线性代数将成为你解决复杂问题的瑞士军刀! 🔧
二、线性代数的核心意义是什么?
核心意义——用数学重构世界的底层逻辑
🌐 意义一:高维世界的解码器
核心作用:将抽象的高维关系转化为可视的几何操作
- 通俗类比:就像给你的大脑装上处理多维数据的"超维度眼镜"
- 典型案例:
- 3D游戏开发:用矩阵乘法实现角色旋转/缩放(每个动作对应一个变换矩阵)
- 量子计算:量子态用希尔伯特空间中的向量描述
- 推荐系统:用户画像=500维向量,电影特征=另一500维向量,点击率预测=向量内积
🔄 意义二:跨学科通用语言
核心作用:提供各领域统一的问题描述框架
- 万物皆可矩阵化:
领域 矩阵应用实例 电路分析 节点电压方程 → 系数矩阵 经济学 投入产出表 → 矩阵平衡模型 社会学 社交网络 → 邻接矩阵 气象学 全球温度场 → 三维张量
⚡ 意义三:复杂系统的切割工具
核心方法:通过矩阵分解解决高复杂度问题
关键技术:
- 特征分解 —— 找出系统核心振动模式
应用场景:桥梁共振分析 → 避免特定频率段载荷 - SVD分解 —— 数据本质特征的提取手术
效果对比:- 原始人脸数据:1000x1000像素 → 100万维度
- 经SVD处理:保留95%信息的特征脸 → 仅需50维度
🚀 意义四:智能时代的发动机
核心支撑:AI算法的底层数学架构
典型应用链:
-
神经网络:权重更新 = 矩阵乘法链
-
单层计算示例:

(W:权重矩阵,X:输入向量,σ:激活函数)
-
-
Transformer架构(ChatGPT核心):
- 自注意力机制 → 计算文本词向量关联度的矩阵运算
- 位置编码 → 将词序信息融入高维空间
🔑 意义五:抽象思维的训练场
核心价值:培养用数学结构剥离问题本质的能力
思维训练示例:
实际问题:疫情期间物资配送路线规划
线性代数思维拆解:
- 将各仓库视为向量(库存量⊗位置坐标)
- 配送需求转化为矩阵(需求量⊗时间窗口)
- 用线性规划求最优解(在约束矩阵条件下优化目标函数)
🔍 价值对照表
| 维度 | 无线性代数思维 | 具备线性代数思维 |
|---|---|---|
| 看数据 | 只见杂乱的数字 | 能洞察向量空间中的分布规律 |
| 解方程 | 硬算多变量方程耗时易错 | 矩阵消元法快速取得精确解 |
| 作预测 | 基于单因素直线预测 | 高维超平面拟合复杂关系 |
| 降维度 | 手工筛选重要特征 | 用PCA自动提取本质维度 |
🖼️ 图示:核心意义关系网
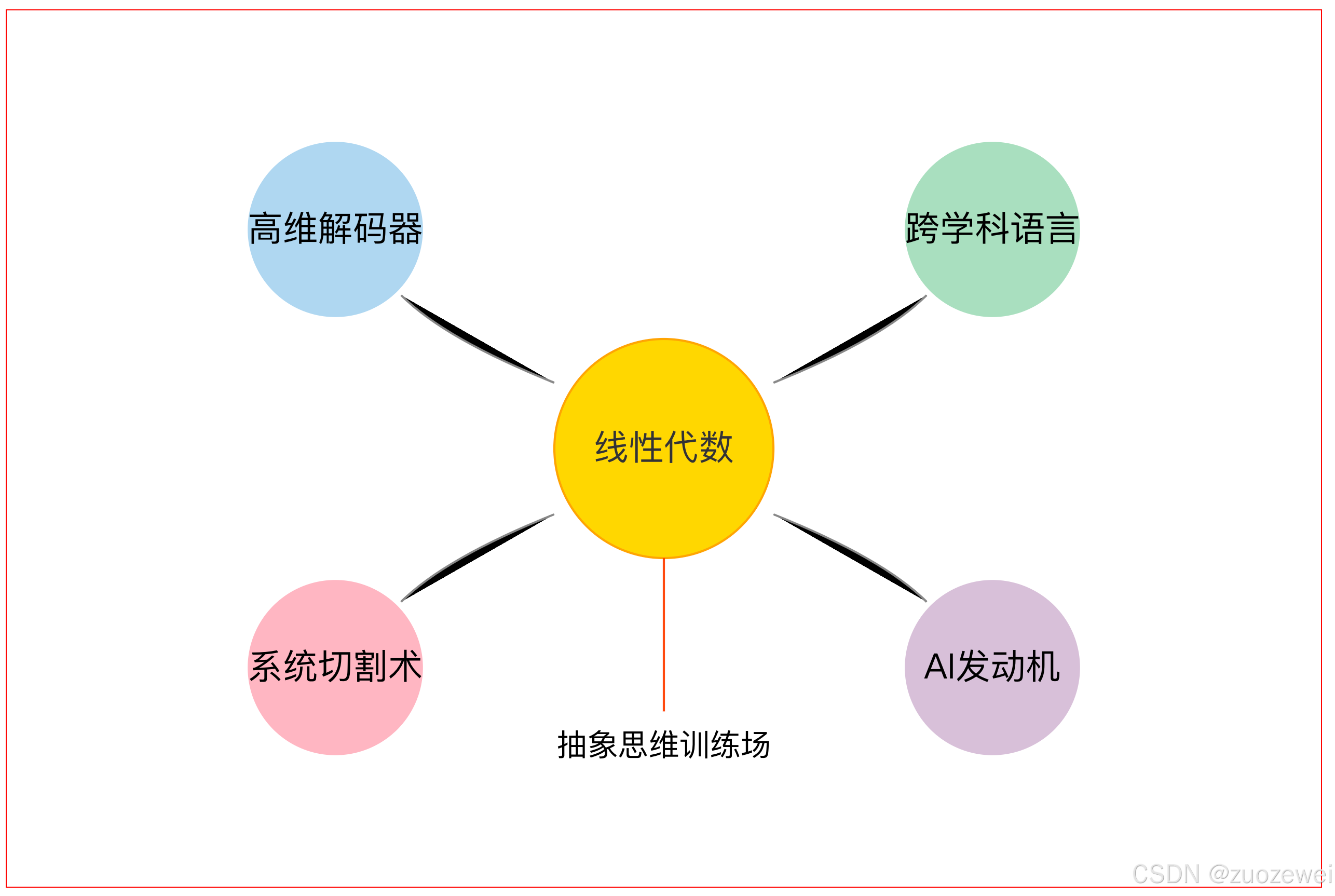
图示解析:
- 黄金中心:线性代数核心地位
- 四大卫星:核心意义的关键方向
- 橙色流动箭头:抽象思维贯穿所有应用
- 颜色编码:
- 蓝:基础理论研究
- 绿:跨领域应用
- 粉:工程技术应用
- 紫:智能算法支撑
💡 最终洞察
学习线性代数不是单纯掌握矩阵运算技巧,而是获得一把通用钥匙,它能:
- 穿透表象:看到数据背后的空间结构
- 打破维度:在复杂系统中抓住主要矛盾
- 预见未来:通过建模预测系统演化趋势
这使它成为现代科技文明的隐形支柱,就像十进制数字系统一样基础而不可或缺。
三、线性代数的基本概念
以下是线性代数核心概念的阶梯式解析:
等级式解析表

详细分步理解
1️⃣ 集合(Set)
- 核心思想:元素的收纳箱
- 关键属性:
- 无序性:{苹果, 香蕉} = {香蕉, 苹果}
- 互异性:禁止重复元素
- 线性代数中的作用:
→ 定义运算的取值范围(如矩阵元素来自实数集ℝ)
2️⃣ 标量(Scalar)
-
操作演示:
单价 = 8.5元(标量) 数量 = 3本 (标量) 总价 = 8.5 × 3 = 25.5元 (标量) -
特殊性质:
→ 坐标系中的缩放因子(如放大3倍即乘标量3)
3️⃣ 向量(Vector)
- 物理视角:
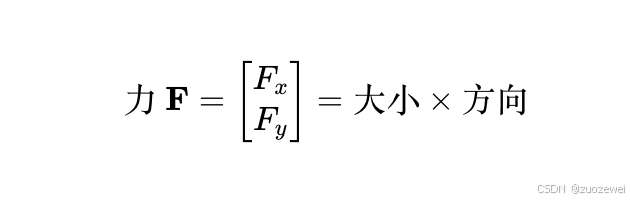
- 数据处理:
→ 用户画像向量:[年龄=25, 消费=8000, 活跃度=0.7]
4️⃣ 矩阵(Matrix)
-
核心操作链:

-
特殊类型:
→ 单位矩阵(乘法不变性):数字世界的"1"
→ 对角矩阵(个体独立操作):VIP单独处理通道
5️⃣ 张量(Tensor)
- 维度扩展法则:
向量(1D)→ 展开成矩阵(2D)→ 堆叠成立方体(3D)→ …# PyTorch张量示例 batch_images = torch.randn(32, 256, 256, 3) # [批次, 高, 宽, 通道] - 经典分解:
CP分解 / Tucker分解 → 挖掘隐藏维度关系
几何演进图示

图示解读:
- 红色点 → 标量的零维度
- 绿色箭头 → 向量的方向性
- 蓝色格子 → 矩阵的二维结构
- 橙色立方体 → 张量的三维扩展
速记口诀
维度发展四部曲:
〇维标量单打独斗,一维向量指路明灯,
二维矩阵排兵布阵,高维张量包罗万象。
数值关系看阶数:
标量是兵(0阶),向量是队(1阶),
矩阵是将(2阶),张量是帅(≥3阶)。
核心联系
这种概念层级构成现代数据处理的基石:
标量 → 嵌入到向量 → 组织成矩阵 → 扩展为张量
每一个升级都意味着:
✅ 更多元的特征表达
✅ 更复杂的相互关系处理
✅ 更强的现实世界建模能力
就如同原子→分子→细胞→生物体的构建过程,线性代数概念体系搭建起了数字宇宙的物质基础。
以下是线性代数在人工智能中的关键应用解析,采用分层递进的方式呈现:
四、线性代数在人工智能中的关键应用
核心作用定位
线性代数之于AI,如同:
- 砖块之于建筑:构成基本结构单元
- 字母之于文字:组成所有表达的基础
- 音符之于乐章:形成复杂系统的元素
分场景应用解析
1️⃣ 神经网络——矩阵运算交响曲
典型过程:
输入层(300维词向量) → 权重矩阵(300×512) → 隐藏层(512维) → 激活函数 → 输出
数学表达式:

关键操作:
- 矩阵乘法:特征空间变换(维度升降)
- 张量积:多模态数据融合(如图文匹配)
- 范数计算:正则化约束(防止过拟合)
生活化类比:
神经网络像多层物流分拣系统,权重矩阵是传送带速度调节器,决定不同特征到达下一层的"优先级"。
2️⃣ 图像处理——维度魔法
典型应用:
卷积核运算(3×3滤波器扫描图像) → 特征图生成 → 池化降维
数学表达:

关键概念:
- 张量存储:图像批次(B×H×W×C)
- 特征值分解:图像压缩(JPEG算法)
- 奇异值分解:去噪处理(低秩近似)
实例演示:
人脸识别中,一张1024×1024图片被转换为4096维特征向量,相当于将图片投影到高维特征空间。
3️⃣ 自然语言处理——语义空间建模
关键技术:
- 词嵌入(Word2Vec):
词→300维向量,使king - man + woman = queen - 注意力机制:
通过QKV矩阵计算关联权重 - 位置编码:
使用正弦函数矩阵注入序列位置信息
矩阵运算示例:
Transformer中的自注意力计算:

4️⃣ 推荐系统——潜在因子挖掘
矩阵分解模型:

优化目标:

现实案例:
Netflix推荐系统通过此方法将用户和影片映射到20维潜空间。
5️⃣ 强化学习——策略优化
价值函数计算:

策略梯度更新:

关键数学工具
线性代数武器库
| 工具 | AI应用场景 | 典型案例 |
|---|---|---|
| 特征分解 | 主成分分析(PCA) | 人脸识别特征降维 |
| 奇异值分解 | 推荐系统矩阵补全 | Netflix用户评分预测 |
| 矩阵求导 | 反向传播算法 | 神经网络参数更新 |
| 张量积 | 多模态数据融合 | 图文匹配(CLIP模型) |
| 范数约束 | 正则化优化 | L2权重衰减防止过拟合 |
三维可视化演示
神经网络前向传播过程

图示解析:
- 粉色块:输入特征向量(如用户行为数据)
- 蓝色网格:神经网络权重矩阵
- 绿色块:经过矩阵乘法后的输出结果
- 运算符号:展示线性变换过程
快速记忆口诀
线性代数三件套,矩阵向量加张量:
矩阵变换改维度,向量存储特征值,
张量处理多维数,AI大厦靠它筑。
特征分解找主轴,奇异分解补残缺,
范数约束防过配,求导反向传误差。
学习路线建议
- 基础阶段:
- 掌握矩阵运算(乘法、转置、逆)
- 理解特征值/向量的物理意义
- 进阶阶段:
- 学习奇异值分解与矩阵近似
- 掌握张量运算规则
- 实战阶段:
- 在PyTorch/TensorFlow中实践自动微分
- 用NumPy实现PCA降维
关键洞见
现代人工智能系统本质上是高维空间中的几何变换引擎:
- 图像识别:将像素空间映射到语义空间
- 机器翻译:建立语言间的线性映射关系
- 推荐系统:在潜空间计算用户与物品距离
就像3D游戏引擎通过矩阵变换构建虚拟世界,AI系统通过线性代数操作构建智能认知空间。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










