矩阵连乘问题

    

   给定有n个连乘矩阵的维数，要求计算其采用最优计算次序时所用的乘法次数，即所要求计算的乘法次数最少。例如，给定三个连乘矩阵{A1，A2，A3}的维数分别是10*100，100*5和5*50，采用（A1A2）A3，乘法次数为10*100*5+10*5*50=7500次，而采用A1（A2A3），乘法次数为100*5*50+10*100*50=75000次乘法，显然，最好的次序是（A1A2)A3，乘法次数为7500次。

输入
输入数据有T组测试数据。测试数据的数目 (T)在输入的第一行给出。每组测试数据的第一行为矩阵个数K，接下来K行，每行两个整数M和N（1<=M,N<=100），表示一个矩阵的维数，维数之间用一空格隔开。输入矩阵的顺序采用连乘的顺序，即可以假定输入符合矩阵连乘。
输出
每个用例，用一行输出采用最优次序得到的最少乘法次数。
样例输入
2
3
10 100
100 5
5 50
1
10 20
样例输出
7500

0

题解：

     

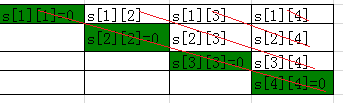
    将每条对角线上的值初始化为0.

    依次求出斜线上的值。

#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
int n,d[1000],s[1000][1000];
int work()
{
    int i,j,k,l;
	for(i=0; i<n; i++)
		s[i][i] = 0;
	for(l=2; l<=n; l++)
	{
		for(i=1; i<=n-l+1; i++)
		{
			j = i+l-1;
			s[i][j] = s[i][i]+s[i+1][j]+d[i-1]*d[i]*d[j];
			for(k=i+1; k<j; k++)
			{
				int temp = s[i][k] + s[k+1][j] +d[i-1]*d[k]*d[j];
				if(temp<s[i][j])
					s[i][j] = temp;
			}
		}
	}
	return s[1][n];
}
int main()
{
	int t,i,j,a,b;
     cin>>t;
	 while(t--)
	 {
		 j=0;
		 cin>>n;
		 for(i=0; i<n-1; i++)
		 {
			 cin>>a>>b;
              d[j++] = a;
		 } 
		 cin>>a>>b;
		 d[j++] = a;
		 d[j++] = b;
		 cout<<work()<<endl;
	 }
   return 0;
}