【Matlab】贝叶斯网络理论之结构学习理论介绍及其工具箱安装

最新推荐文章于 2023-02-19 15:24:08 发布

CallMeJacky

最新推荐文章于 2023-02-19 15:24:08 发布

阅读量3.9k

点赞数 1

分类专栏： Matlab编程与绘图文章标签：贝叶斯网结构学习统计学

本文链接：https://blog.csdn.net/zyxhangiian123456789/article/details/85790657

版权

Matlab编程与绘图专栏收录该内容

44 篇文章

订阅专栏

1.结构学习的定义

即寻找对数据拟合最好的贝叶斯网络结构。

例如：独立抛掷两枚硬币 X 与 Y，共20次。观察到：3次正面/正面，6次正面/反面，5次反面/正面，6次反面/反面。用贝叶斯公式计算，可得到：
P ( X = 正面 ) = 0.45；
P ( Y = 正面 | X = 正面 ) = 1/3；
P ( Y = 正面 | X = 反面 ) = 5/11

由 Y 的条件概率可以计算得到它的边缘概率为
P ( Y = 正面 ) = P ( Y = 正面 | X = 正面 )
+ P ( Y = 正面 | X = 反面 )
= 1/3 + 5/11 = 26/33 （约等于0.79）
而如果按照 Y 是独立变量来计算的话，
P ( Y = 正面 ) = 8/20 = 0.4

为了拟合20次实验的数据，算法会在 X 和 Y 之间添加一个边，使得学习得到的贝叶斯网结构中 X 和 Y 存在依赖关系。但是，硬币抛掷是独立事件，X 和 Y 之间不应该相关。因此，学习目标为包含尽量少的边，又能较好拟合数据的结构模型。

2.三种无验知识的结构学习方法

a) 基于约束的结构学习。

通过对数据中的条件依赖或独立关系进行检验，找到解释最好的网络结构，具有规则简单、易于实现且学习效果相对较好，其时间复杂度不会随着网络结构中节点数目的增加而上升。通过条件独立检验来确定边的存在与否，从而确定贝叶斯网路的框架。然后根据独立检验中产生的分割集确定边的方向，从而得到贝叶斯网络结构模型。

基于约束的学习方法之一就是通过卡方统计量做假设检验，通过样本落入的区域来确定是否拒绝独立性假设，若样本统计量掉落在拒绝域内，则拒绝独立性，否则不拒绝。实施步骤如下：

1.建立假设；
2.构造的卡方统计值，给出拒绝域；
3.选择显著性水平；
4.计算统计量，并通过比较确定是否接受原假设。
通常，显著性水平 α 的值域一般取作[0.0001,0.05]，其意义是衡量了拒绝原假设的正确性为 1 - α。

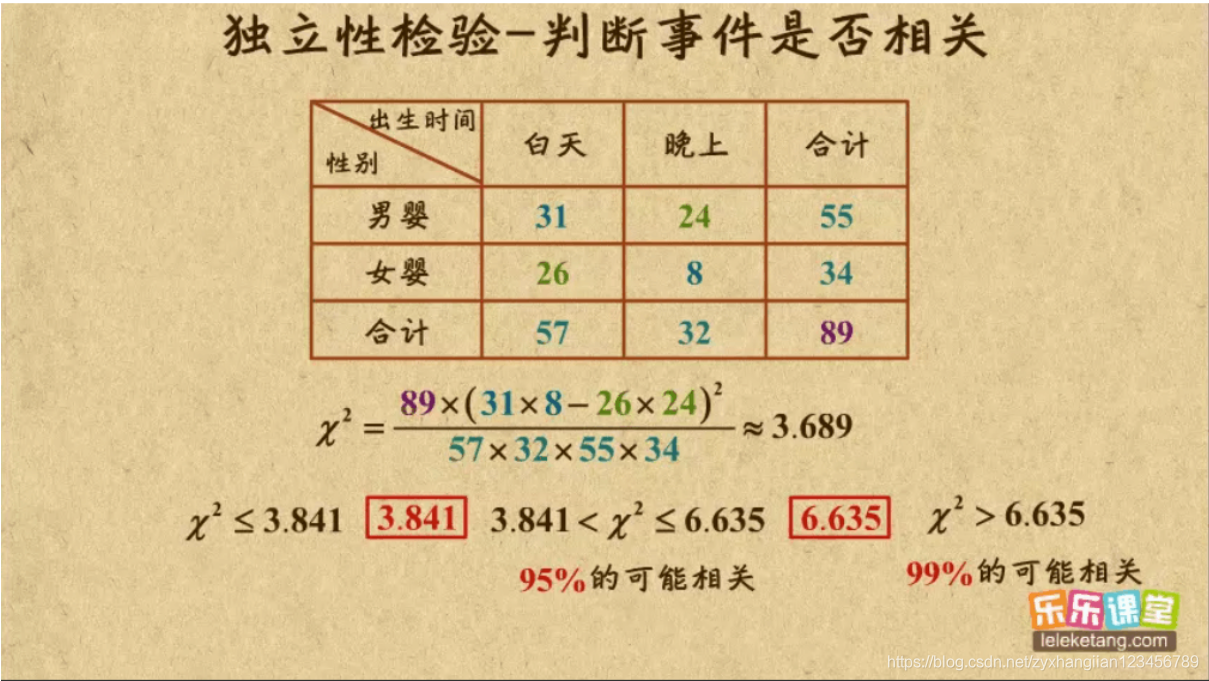
下图是一个利用卡方检验分析事件A：生男生女和事件B：白天晚上之间是否存在关系的例子。

b) 基于得分的结构学习。

基于得分的方法把结构学习问题作为一个优化问题来解决。定义贝叶斯网的统计得分，然后借助启发式搜索技术找到最高分的结构。

定义一个得分函数，根据训练数据对每个候选结构打分，然后搜索得到一个得分高的结构。常用的得分函数有：贝叶斯得分、CH评分标准、BIC评分标准、MDL评分标准、AIC评分标准、HVL评分标准和CVL评分标准等。

常用的搜索算法是启发式局部搜索算法，这种方法从给定的初始网络结构 ( 可以是空网络结构、随机指定的网络结构、先验网络结构等 ) 开始，通过增加、删除和转向操作使得局部最大化，再逐渐扩展到整个网络。
- K2算法：通过逐渐加边寻找评分高的模型；
- 爬山法：利用搜索算子逐步对模型做局部修改；
- 结构EM算法：当数据有缺失值时对结构和参数同时优化。

K2算法为简化模型评分的计算，K2假设所有参数先验分布都是均匀分布。

爬山法：首先，从无边模型出发，利用搜索算子 ( 加边、减边、转边 ) 对当前模型进行局部修改 ( 不能形成有向圈 ) ，得到一系列候选模型；接着，计算每个候选模型的评分，将其中分数最高的模型的评分与修改前的模型比较，选择评分高的作为当前模型。