/*
*Copyright (c) 2015 , 烟台大学计算机学院
*All right resvered .
*文件名称:查找——B-树的基本操作.cpp
*作 者: 郑兆涵
*查找——B-树的基本操作
*/ 问题:实现B-树的基本操作。基于序列{4, 9, 0, 1, 8, 6, 3, 5, 2, 7}完成测试。
(1)创建对应的3阶B-树b,用括号法输出b树。
(2)从b中分别删除关键字为8和1的节点,用括号法输出删除节点后的b树。
编程代码:
#include <stdio.h>
#include <malloc.h>
#define MAXM 10 //定义B-树的最大的阶数
typedef int KeyType; //KeyType为关键字类型
typedef struct node //B-树结点类型定义
{
int keynum; //结点当前拥有的关键字的个数
KeyType key[MAXM]; //key[1..keynum]存放关键字,key[0]不用
struct node *parent; //双亲结点指针
struct node *ptr[MAXM]; //孩子结点指针数组ptr[0..keynum]
} BTNode;
typedef struct //B-树的查找结果类型
{
BTNode *pt; //指向找到的结点
int i; //1..m,在结点中的关键字序号
int tag; //1:查找成功,O:查找失败
} Result;
int m; //m阶B-树,为全局变量
int Max; //m阶B-树中每个结点的至多关键字个数,Max=m-1
int Min; //m阶B-树中非叶子结点的至少关键字个数,Min=(m-1)/2
int Search(BTNode *p,KeyType k)
{
//在p->key[1..keynum]中查找i,使得p->key[i]<=k<p->key[i+1]
int i=0;
for(i=0; i<p->keynum && p->key[i+1]<=k; i++);
return i;
}
Result SearchBTree(BTNode *t,KeyType k)
{
/*在m阶t树t上查找关键字k,返回结果(pt,i,tag)。若查找成功,则特征值
tag=1,指针pt所指结点中第i个关键字等于k;否则特征值tag=0,等于k的
关键字应插入在指针Pt所指结点中第i和第i+1个关键字之间*/
BTNode *p=t,*q=NULL; //初始化,p指向待查结点,q指向p的双亲
int found=0,i=0;
Result r;
while (p!=NULL && found==0)
{
i=Search(p,k); //在p->key[1..keynum]中查找i,使得p->key[i]<=k<p->key[i+1]
if (i>0 && p->key[i]==k) //找到待查关键字
found=1;
else
{
q=p;
p=p->ptr[i];
}
}
r.i=i;
if (found==1) //查找成功
{
r.pt=p;
r.tag=1;
}
else //查找不成功,返回K的插入位置信息
{
r.pt=q;
r.tag=0;
}
return r; //返回k的位置(或插入位置)
}
void Insert(BTNode *&q,int i,KeyType x,BTNode *ap)
{
//将x和ap分别插入到q->key[i+1]和q->ptr[i+1]中
int j;
for(j=q->keynum; j>i; j--) //空出一个位置
{
q->key[j+1]=q->key[j];
q->ptr[j+1]=q->ptr[j];
}
q->key[i+1]=x;
q->ptr[i+1]=ap;
if (ap!=NULL) ap->parent=q;
q->keynum++;
}
void Split(BTNode *&q,BTNode *&ap)
{
//将结点q分裂成两个结点,前一半保留,后一半移入新生结点ap
int i,s=(m+1)/2;
ap=(BTNode *)malloc(sizeof(BTNode)); //生成新结点*ap
ap->ptr[0]=q->ptr[s]; //后一半移入ap
for (i=s+1; i<=m; i++)
{
ap->key[i-s]=q->key[i];
ap->ptr[i-s]=q->ptr[i];
if (ap->ptr[i-s]!=NULL)
ap->ptr[i-s]->parent=ap;
}
ap->keynum=q->keynum-s;
ap->parent=q->parent;
for (i=0; i<=q->keynum-s; i++) //修改指向双亲结点的指针
if (ap->ptr[i]!=NULL) ap->ptr[i]->parent = ap;
q->keynum=s-1; //q的前一半保留,修改keynum
}
void NewRoot(BTNode *&t,BTNode *p,KeyType x,BTNode *ap)
{
//生成含信息(T,x,ap)的新的根结点*t,原t和ap为子树指针
t=(BTNode *)malloc(sizeof(BTNode));
t->keynum=1;
t->ptr[0]=p;
t->ptr[1]=ap;
t->key[1]=x;
if (p!=NULL) p->parent=t;
if (ap!=NULL) ap->parent=t;
t->parent=NULL;
}
void InsertBTree(BTNode *&t, KeyType k, BTNode *q, int i)
{
/*在m阶t树t上结点*q的key[i]与key[i+1]之间插入关键字k。若引起
结点过大,则沿双亲链进行必要的结点分裂调整,使t仍是m阶t树。*/
BTNode *ap;
int finished,needNewRoot,s;
KeyType x;
if (q==NULL) //t是空树(参数q初值为NULL)
NewRoot(t,NULL,k,NULL); //生成仅含关键字k的根结点*t
else
{
x=k;
ap=NULL;
finished=needNewRoot=0;
while (needNewRoot==0 && finished==0)
{
Insert(q,i,x,ap); //将x和ap分别插入到q->key[i+1]和q->ptr[i+1]
if (q->keynum<=Max) finished=1; //插入完成
else
{
//分裂结点*q,将q->key[s+1..m],q->ptr[s..m]和q->recptr[s+1..m]移入新结点*ap
s=(m+1)/2;
Split(q,ap);
x=q->key[s];
if (q->parent) //在双亲结点*q中查找x的插入位置
{
q=q->parent;
i=Search(q, x);
}
else needNewRoot=1;
}
}
if (needNewRoot==1) //根结点已分裂为结点*q和*ap
NewRoot(t,q,x,ap); //生成新根结点*t,q和ap为子树指针
}
}
void DispBTree(BTNode *t) //以括号表示法输出B-树
{
int i;
if (t!=NULL)
{
printf("["); //输出当前结点关键字
for (i=1; i<t->keynum; i++)
printf("%d ",t->key[i]);
printf("%d",t->key[i]);
printf("]");
if (t->keynum>0)
{
if (t->ptr[0]!=0) printf("("); //至少有一个子树时输出"("号
for (i=0; i<t->keynum; i++) //对每个子树进行递归调用
{
DispBTree(t->ptr[i]);
if (t->ptr[i+1]!=NULL) printf(",");
}
DispBTree(t->ptr[t->keynum]);
if (t->ptr[0]!=0) printf(")"); //至少有一个子树时输出")"号
}
}
}
void Remove(BTNode *p,int i)
//从*p结点删除key[i]和它的孩子指针ptr[i]
{
int j;
for (j=i+1; j<=p->keynum; j++) //前移删除key[i]和ptr[i]
{
p->key[j-1]=p->key[j];
p->ptr[j-1]=p->ptr[j];
}
p->keynum--;
}
void Successor(BTNode *p,int i)
//查找被删关键字p->key[i](在非叶子结点中)的替代叶子结点
{
BTNode *q;
for (q=p->ptr[i]; q->ptr[0]!=NULL; q=q->ptr[0]);
p->key[i]=q->key[1]; //复制关键字值
}
void MoveRight(BTNode *p,int i)
//把一个关键字移动到右兄弟中
{
int c;
BTNode *t=p->ptr[i];
for (c=t->keynum; c>0; c--) //将右兄弟中所有关键字移动一位
{
t->key[c+1]=t->key[c];
t->ptr[c+1]=t->ptr[c];
}
t->ptr[1]=t->ptr[0]; //从双亲结点移动关键字到右兄弟中
t->keynum++;
t->key[1]=p->key[i];
t=p->ptr[i-1]; //将左兄弟中最后一个关键字移动到双亲结点中
p->key[i]=t->key[t->keynum];
p->ptr[i]->ptr[0]=t->ptr[t->keynum];
t->keynum--;
}
void MoveLeft(BTNode *p,int i)
//把一个关键字移动到左兄弟中
{
int c;
BTNode *t;
t=p->ptr[i-1]; //把双亲结点中的关键字移动到左兄弟中
t->keynum++;
t->key[t->keynum]=p->key[i];
t->ptr[t->keynum]=p->ptr[i]->ptr[0];
t=p->ptr[i]; //把右兄弟中的关键字移动到双亲兄弟中
p->key[i]=t->key[1];
p->ptr[0]=t->ptr[1];
t->keynum--;
for (c=1; c<=t->keynum; c++) //将右兄弟中所有关键字移动一位
{
t->key[c]=t->key[c+1];
t->ptr[c]=t->ptr[c+1];
}
}
void Combine(BTNode *p,int i)
//将三个结点合并到一个结点中
{
int c;
BTNode *q=p->ptr[i]; //指向右结点,它将被置空和删除
BTNode *l=p->ptr[i-1];
l->keynum++; //l指向左结点
l->key[l->keynum]=p->key[i];
l->ptr[l->keynum]=q->ptr[0];
for (c=1; c<=q->keynum; c++) //插入右结点中的所有关键字
{
l->keynum++;
l->key[l->keynum]=q->key[c];
l->ptr[l->keynum]=q->ptr[c];
}
for (c=i; c<p->keynum; c++) //删除父结点所有的关键字
{
p->key[c]=p->key[c+1];
p->ptr[c]=p->ptr[c+1];
}
p->keynum--;
free(q); //释放空右结点的空间
}
void Restore(BTNode *p,int i)
//关键字删除后,调整B-树,找到一个关键字将其插入到p->ptr[i]中
{
if (i==0) //为最左边关键字的情况
if (p->ptr[1]->keynum>Min)
MoveLeft(p,1);
else
Combine(p,1);
else if (i==p->keynum) //为最右边关键字的情况
if (p->ptr[i-1]->keynum>Min)
MoveRight(p,i);
else
Combine(p,i);
else if (p->ptr[i-1]->keynum>Min) //为其他情况
MoveRight(p,i);
else if (p->ptr[i+1]->keynum>Min)
MoveLeft(p,i+1);
else
Combine(p,i);
}
int SearchNode(KeyType k,BTNode *p,int &i)
//在结点p中找关键字为k的位置i,成功时返回1,否则返回0
{
if (k<p->key[1]) //k小于*p结点的最小关键字时返回0
{
i=0;
return 0;
}
else //在*p结点中查找
{
i=p->keynum;
while (k<p->key[i] && i>1)
i--;
return(k==p->key[i]);
}
}
int RecDelete(KeyType k,BTNode *p)
//查找并删除关键字k
{
int i;
int found;
if (p==NULL)
return 0;
else
{
if ((found=SearchNode(k,p,i))==1) //查找关键字k
{
if (p->ptr[i-1]!=NULL) //若为非叶子结点
{
Successor(p,i); //由其后继代替它
RecDelete(p->key[i],p->ptr[i]); //p->key[i]在叶子结点中
}
else
Remove(p,i); //从*p结点中位置i处删除关键字
}
else
found=RecDelete(k,p->ptr[i]); //沿孩子结点递归查找并删除关键字k
if (p->ptr[i]!=NULL)
if (p->ptr[i]->keynum<Min) //删除后关键字个数小于MIN
Restore(p,i);
return found;
}
}
void DeleteBTree(KeyType k,BTNode *&root)
//从B-树root中删除关键字k,若在一个结点中删除指定的关键字,不再有其他关键字,则删除该结点
{
BTNode *p; //用于释放一个空的root
if (RecDelete(k,root)==0)
printf(" 关键字%d不在B-树中\n",k);
else if (root->keynum==0)
{
p=root;
root=root->ptr[0];
free(p);
}
}
int main()
{
BTNode *t=NULL;
Result s;
int j,n=10;
KeyType a[]= {4,9,0,1,8,6,3,5,2,7},k;
m=3; //3阶B-树
Max=m-1;
Min=(m-1)/2;
printf("创建一棵%d阶B-树:\n",m);
for (j=0; j<n; j++) //创建一棵3阶B-树t
{
s=SearchBTree(t,a[j]);
if (s.tag==0)
InsertBTree(t,a[j],s.pt,s.i);
printf(" 第%d步,插入%d: ",j+1,a[j]);
DispBTree(t);
printf("\n");
}
printf(" 结果B-树: ");
DispBTree(t);
printf("\n");
printf("删除操作:\n");
k=8;
DeleteBTree(k,t);
printf(" 删除%d: ",k);
printf("B-树: ");
DispBTree(t);
printf("\n");
k=1;
DeleteBTree(k,t);
printf(" 删除%d: ",k);
printf("B-树: ");
DispBTree(t);
printf("\n");
return 0;
}
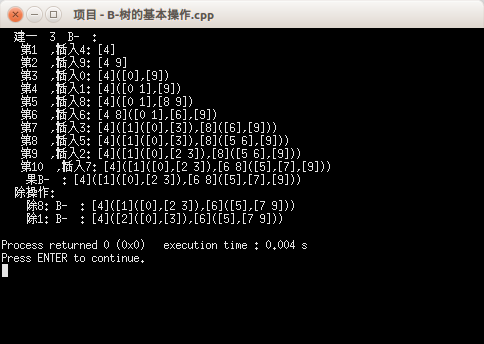
输出结果:
学习心得:
顺序查找和二分查找都是静态查找,而二叉排序树和平衡二叉树都是内部动态查找,其查找的数据量小,且在内存中完成.B树用作外部查找,也称为多路平衡查找树,是一种组织和维护外村文件系统非常有效的数据结构.
B-树中所有节点的孩子节点树的最大值称为B-树的阶,通常用m表示,从查找效率考虑,要求m≥3.一棵m阶B-树或者是一棵空树,或者是满足以下要求的m叉树:
(1)所有的叶子节点在同一层,并且不带信息;
(2)树中每个节点至多由m棵子树(即至多含有m-1个关键字);
(3)若根节点不是终端节点,则根节点至少由两棵子树;
(4)除根节点外,其他非叶子节点至少由m/2取上阶棵子树(即至少含有m/2取上阶减1哥关键字);
在B-树中叶子节点不带信息(可以看做是外部节点或查找失败的节点,实际上这些节点不存在,指向这些节点的指针为空).
B-树的查找:
在B-树中查找给定关键字的方法类似于二叉排序树上的查找,不同的是在每个节点上确定下查找的路径不一定是二路的,而是n+1路的.因为节点内的关键字序列key[1..n]有序,故既可以用顺序查找,也可以用折半查找.在一棵B-树上查找关键字为k的方法为:将k与根节点中的key[i]进行比较:
(1)若k=key[i],则查找成功;
(2)若k<key[1],则沿着指针ptr[0]所指的子树继续查找;
(3)若key[i]<k<key[i+1],则沿着指针ptr[i]所指的子树继续查找;
(4)若k>key[n],则沿着指针ptr[n]所指的子树继续查找.
B-树的插入:
将关键字k插入到B-树的过程分为两步:
(1)利用前述的B-树的查找算法找出该关键字的插入节点(注意B-树的插入节点一定属于最低非叶子节点层).
(2)判断该节点是否还有空位置,即判断该节点是否满足n<m-1,若该节点满足n<m-1,说明该节点还有空位置,直接把关键字k插入到该节点的合适位置上即可(即满足插入后节点上的关键字扔保持有序);若有n=m-1,说明该节点已没有空位置,需要把节点分裂成两个.分裂的做法是,取一新节点,把原节点上的关键字和k按升序排序后,从中间位置(即m/2取上阶处)把关键字(不包括中间位置的关键字)分成两部分,左部分所含关键字放在旧节点中,右部分所含关键字放在新节点中,中间位置的关键字连同新节点的存储位置插入到双亲节点中.如果双亲节点的关键字个数也查过Max,则要再分裂,再网上插,直至这个过程传到根节点为止.
B-树的生成就是从一棵空树开始,逐个插入关键字.
B-树的删除:
B-树的删除过程与插入过程类似,要使删除后节点中的关键字个数≥m/2取上阶-1,涉及节点的合并问题.在B-树上产出关键字k的过程分两步:
(1)利用前述的B-树的查找算法找出该关键字所在的节点.
(2)在节点上删除关键字k分两种情况:一种是在最低非叶子节点层的节点上删除关键字;另一种是在其他非叶子节点上删除关键字.在其他非叶子节点上删除关键字的过程:假设要删除关键字key[i](1≤i≤n),在删去该关键字后,以该节点ptr[i]所指子树中的最小关键字key[min]来代替被删关键字(注意ptr[i]所指子树中的最小关键字key[min]一定是在叶子节点上的),然后再以指针ptr[i]所指节点为根节点查找并删除key[min](即以ptr[i]所指节点为B-树的根节点,以key[min]为要删除的关键字,再次调用B-树上的删除算法),这样也就把在其他非叶子节点上删除关键字k的问题转化成了在最低非叶子节点层的节点上删除关键字key[min]的问题.在B-树的最低非叶子节点层的节点上删除关键字共有三种情况:
①加入被删节点的关键字个数大于Min(m/2取上阶),说明删去该关键字后对应节点扔满足B-树的定义,则可直接删去该关键字.
②加入被删节点的关键字个数等于Min,说明删去该关键字后对应节点将不满足B-树的定义,此时若该节点的左(右)兄弟节点中的关键字个数大于Min,则把该节点的左(右)兄弟节点中最大(最小)的关键字上移到双亲节点中,同时把双亲节点中大于(小于)上移关键字的关键字下移到要删除关键字的节点中,这样删去关键字k后该节点以及它的左(右)兄弟节点都仍旧满足B-树的定义.
③加入被删节点的关键字个数等于Min,并且该节点的左和右兄弟节点(如果存在的话)中关键字个数均等于Min,这时,需把要删除关键字的节点与其左(右)兄弟节点以及双亲节点中分割二者的关键字合并成一个节点,如果因此使双亲节点中关键字个数小于Min,则对双亲节点左同样处理,以至于可能知道对根节点左这样的处理而使整个树减少一层.
B+树:
在索引文件组织中,经常使用B-树的一些变形,其中B+树是一种应用广泛的变形.
(1)每个分支节点至多由m棵子树.
(2)根节点或者没有子树,或者至少由两棵子树.
(3)除根节点外,其他每个分支节点至少由m/2取上阶棵子树.
(4)由n棵子树的节点有n个关键字.
(5)所有叶子节点包含全部关键字及指向相应记录的指针,而且叶子节点按关键字大小顺序链接(可以把每个叶子节点看成是一个基本索引块,它的指针不再指向另一级索引块,而是直接指向数据文件中的记录).
(6)所有分支节点(可看成是索引的索引)中仅包含它的各个子节点(即下级索引的索引块)中最大关键字及指向子节点的指针.
B+树的查找
在B+树中可以采用两种查找方式,一种是直接从最小关键字开始进行顺序查找,另一种是从B+树的根节点开始进行随机超赵.后一种查找方式与B-树的查找方法相似,只是在分支节点上的关键字与查找值相等时,查找并不结束,要继续查到叶子节点为止,此时若查找成功,则按所给指针取出对应元素.因此,在B+树中,不管查找成功与否,每次查找都是经过了一条从树根节点到叶子节点的路径.
B+树的插入
与B-树的插入操作相似,B+树的插入也从叶子节点开始,当插入后节点中的关键字个数大于m时要分裂成两个节点,它们所含关键字个数分别为(m+1)/2取上阶和(m+1)/2取下阶, 同时要使它们的双亲节点中包含由这两个节点的最大关键字和指向这两个节点的指针.若双亲节点的关键字个数大于m,应继续分裂,以此类推.
B+树的删除
B+树的删除也是从叶子节点开始,当叶子节点中最大关键字被删除时,分支节点中的值可以作为"分界关键字"存在.若因删除操作而使节点中关键字个数少于m/2取下阶时,则从兄弟节点中调剂关键字或将该节点和兄弟节点合并,其过程和B-树的删除操作相似.






















 1061
1061

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








