FZU 寒假ACM作业 （三）

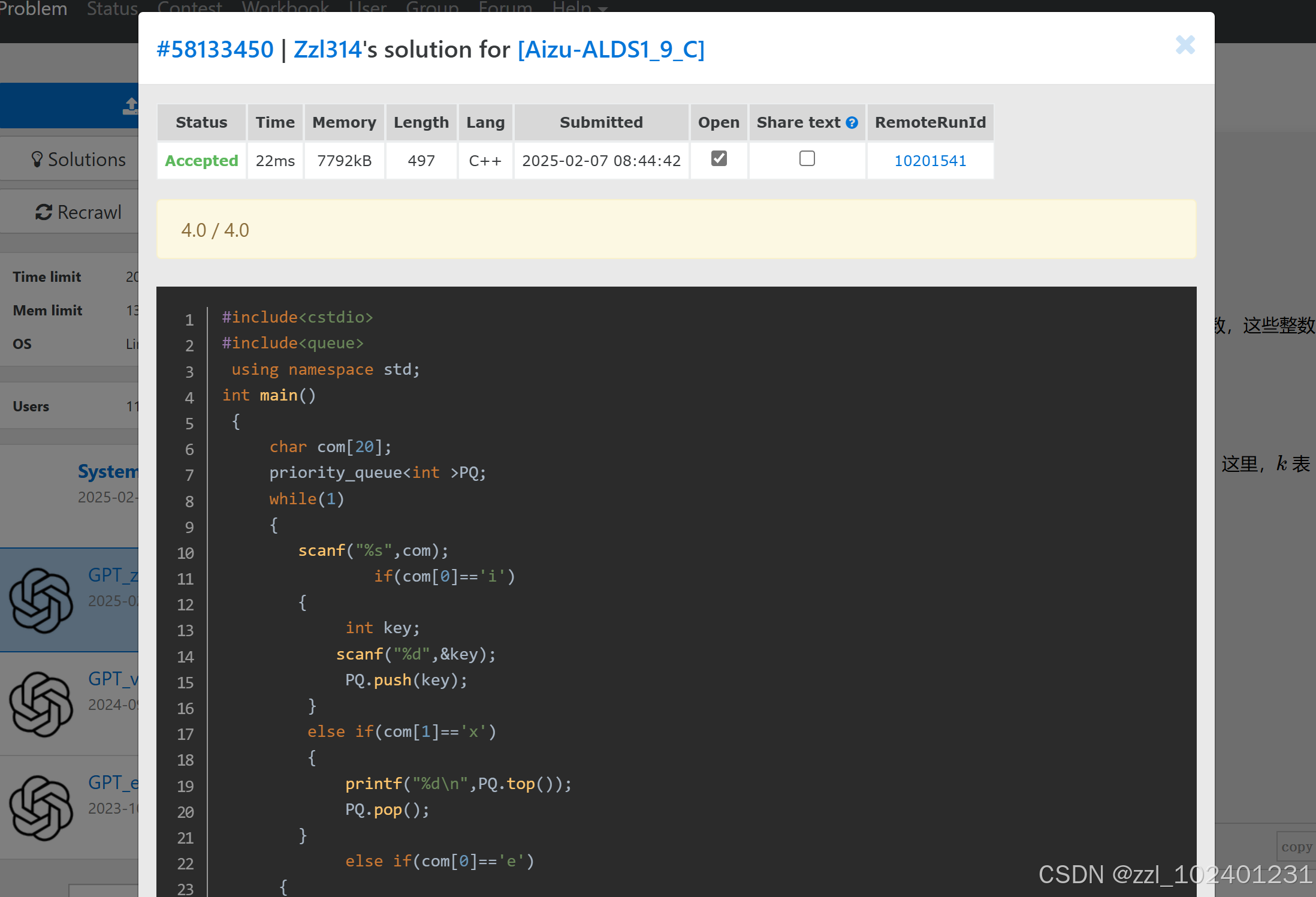
第一题：用queue队列的push和pop匹配插入和返回最大值操作，判断输入的是什么单词，然后做出对应操作，end跳出循环。

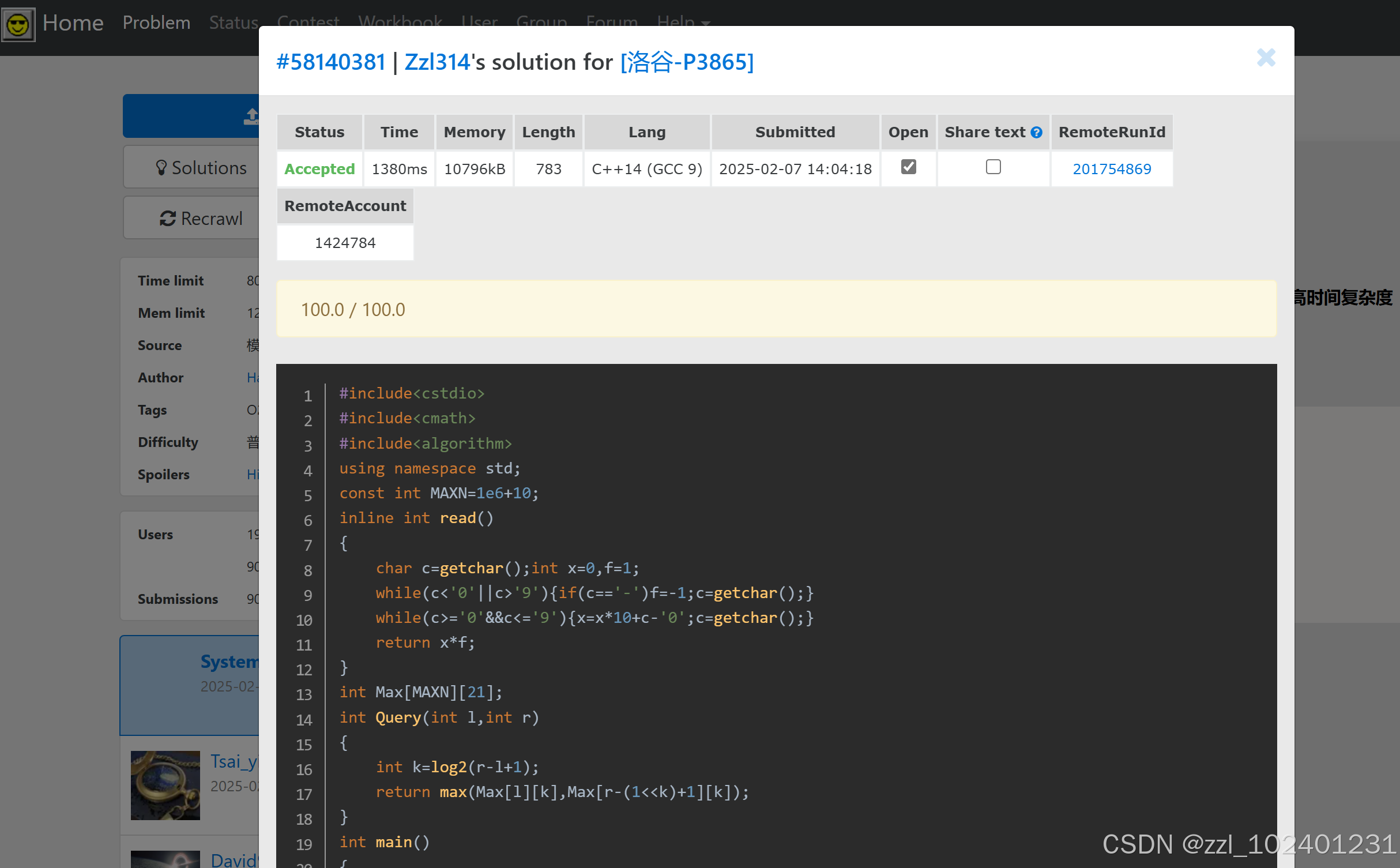第二题：ST 模版，因为时间很严格，所以可以用快速读入

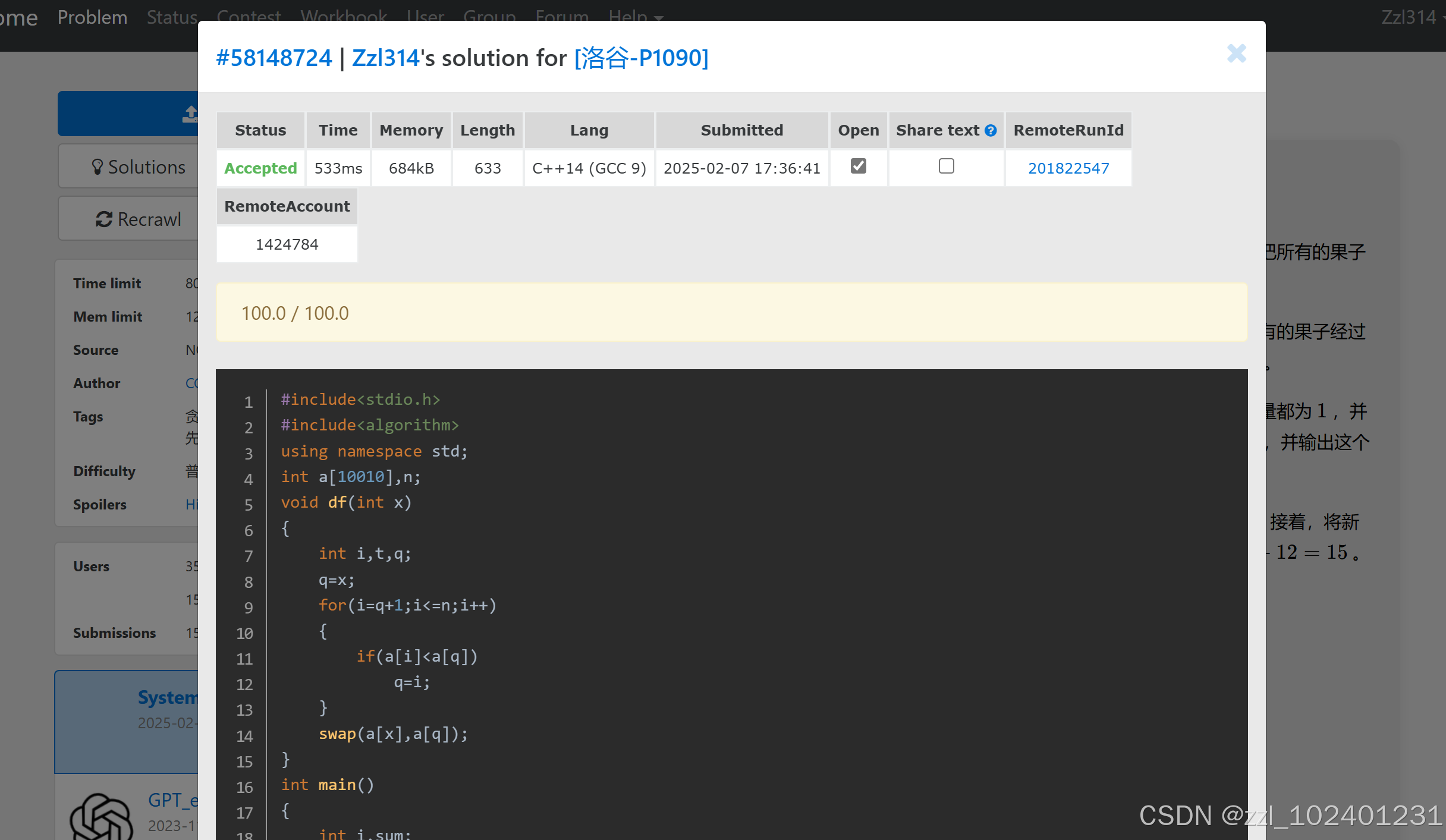
第三题：先找到两个最小的，取出来，相加再放进去，不排序直接找到最小的和次小的，把它们相加再放进去，这样就省下来排序的时间。

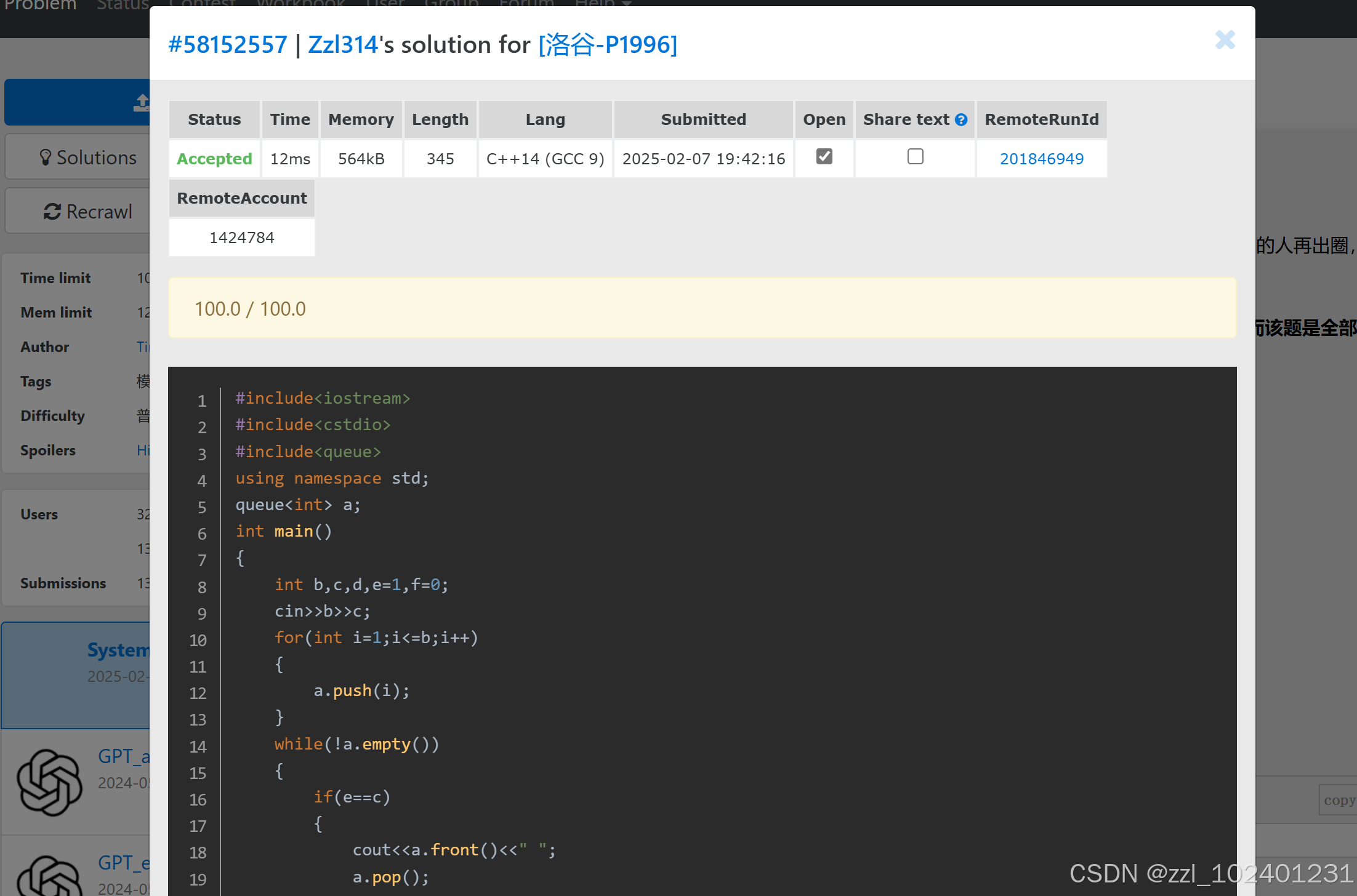
第四题：

首先需要模拟一个队列，将所有的元素压进队列，在进行循环，直到队列为空为止，队列只可以在head删除，那么这就要求我们只要这个人经过判断并且不会被剔除，那么就必须把他排在队尾，若这个人正好被剔除，那先输出他，再踢除。

第五题：

可以构建一个单调递减栈。每次输入一个数a就while判断a是否比原来栈顶的数大。如果比栈顶的数大就证明这个a是之前栈顶数的仰望对象，记录它的仰望对象并将原来栈顶的数出栈。之后再将a进栈。最后将记录的仰望对象输出。

第六题：首先，题目的基础模型类似于线段覆盖，然而题目的背景是环，不能直接操作，所以要“断环成链”，具体做法是将所有区间复制一份，左右端点统一加上 M，如果右端点小于左端点，即在环上走了超过半圈的区间，则先给右端点加上 M再复制。再在这 2∗N 个区间中做贪心。根据线段覆盖的贪心策略，需要先以右端点为关键字排序，复制后无需再排序，因为复制出来的仍然保持有序。

那么如果只用做一次我们就会了，只要选出来的区间总长度达到 M 即可，因为无论是怎样的一个区间，在原本的环上都是以某个点为起点覆盖了整个环。

但是题目的要求要做 N 次，这样做时间复杂度 O(N2) ，显然不行。做每次 O(1) 显然不现实，所以猜测每次操作要降到 O(logN) 。现在面对的问题是如何知道某个区间后选的第 2x个区间究竟是哪个，这需要预处理。如果定义 f[ i ][ j ]表示根据贪心策略，第 i个区间后的第 2j个区间，那么可以得到一个递推关系： f[ i ][ j ]=f[f[ i ][ j−1 ]][ j−1 ]，最后，可以在存区间时在结构体里放一个初始编号，把每次算出的答案放进 ans[ idi]即可。

总结：

倍增使用的场合：

1.同一件事完成多次。

2.当“一次做一件事”可以优化为“一次做多件事”。

双指针扫描的应用：

两个指针代表的内容均只增不减。