NOI2014购票

这是NOIday2压轴题了,粗看之下不就就是树形dp吗?

$$s[x]=min\{s[t]+p[x](l[x]-l[t])\}+q[x],(t\in x.fathers)$$
一看n的大小:200000,哎啊妈呀 $O(n^2)$TLE,得赶紧找优化:
设 $k$为$j$在树上的子孙结点,若有 $$s[k]+p[x](l[x]-l[k])<s[j]+p[x](l[x]-l[j])$$
也即: $$s[k]-s[j]<p[x](l[k]-l[j])\Leftrightarrow\frac{s[k]-s[j]}{l[k]-l[j]}<p[x]$$
我们看到了什么?对,斜率优化.
这样,我们在计算 $s[x]$时就需要维护一个凸包了.凸包上的点以 $l[x]$为横坐标,以 $s[x]$为纵坐标,当然对根也即 $1$结点,它就是原点$(0,0)$

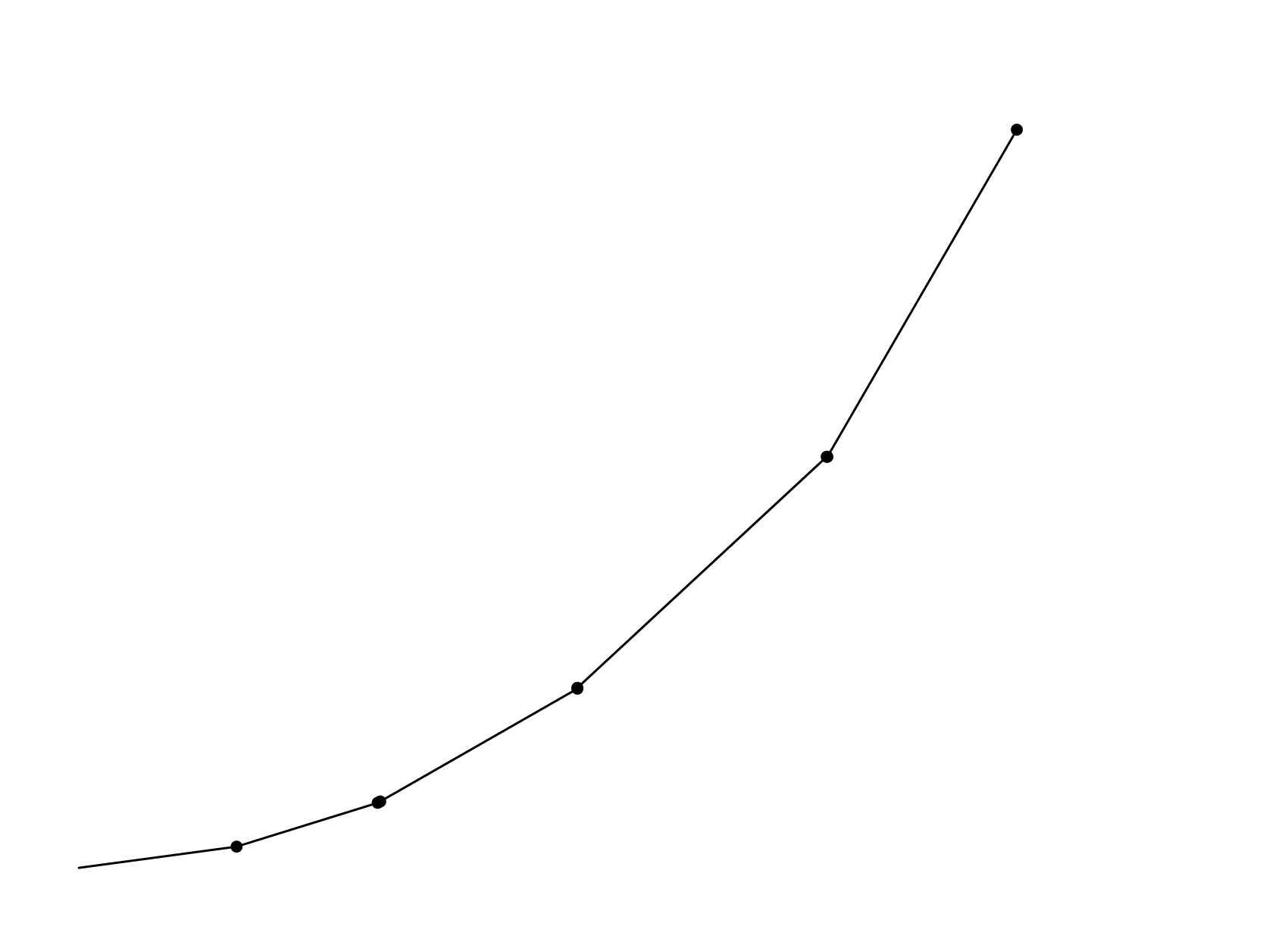
这是一个凸包(省略了坐标轴)
到这里,我们再回顾下题目,什么!?还有距离限制!那么等于说我们不能只简单的维护一个凸包了,这对我们来说是个打击.不过没关系,我们加上距离限制,那么我们只能使用凸包的一段…不仔细想一下,当我们截去凸包的一段时,有可能加入新的可行点!
我们从红色箭头所指的地方截断凸包,但我们发现,原来插入结点时所删去的两个结点是有可能作为答案的!例如:
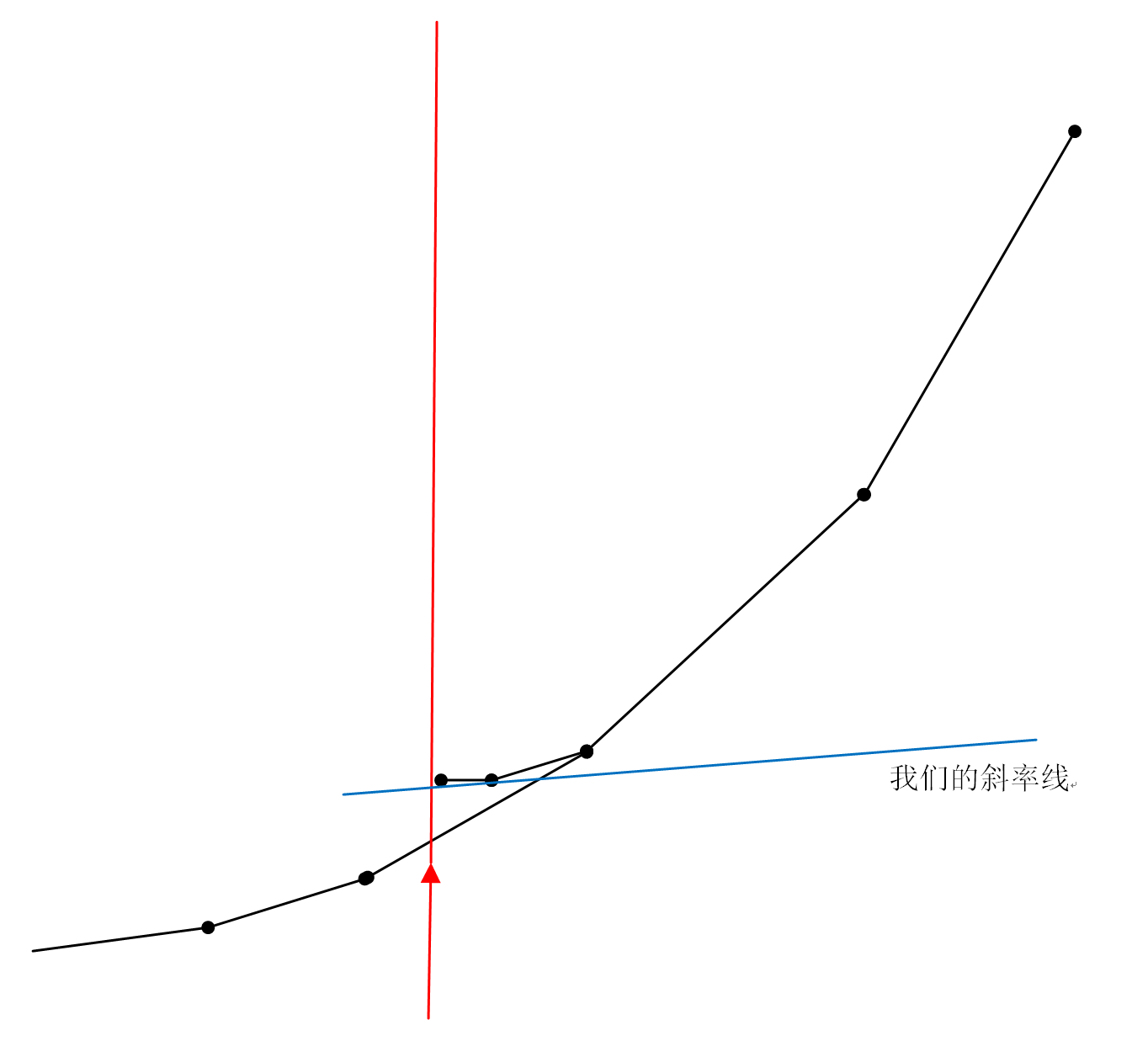
在这里,我们发现新加入的第二个点就是答案因此,我们所面对的问题在加入了距离限制后变得棘手的多了,当然,这也是此题的魅力所在.
我们来考虑这个问题怎么处理:
凸包是可合并的,即我们从两个凸包中分别获得了答案但最后,我们选择了上面的结点

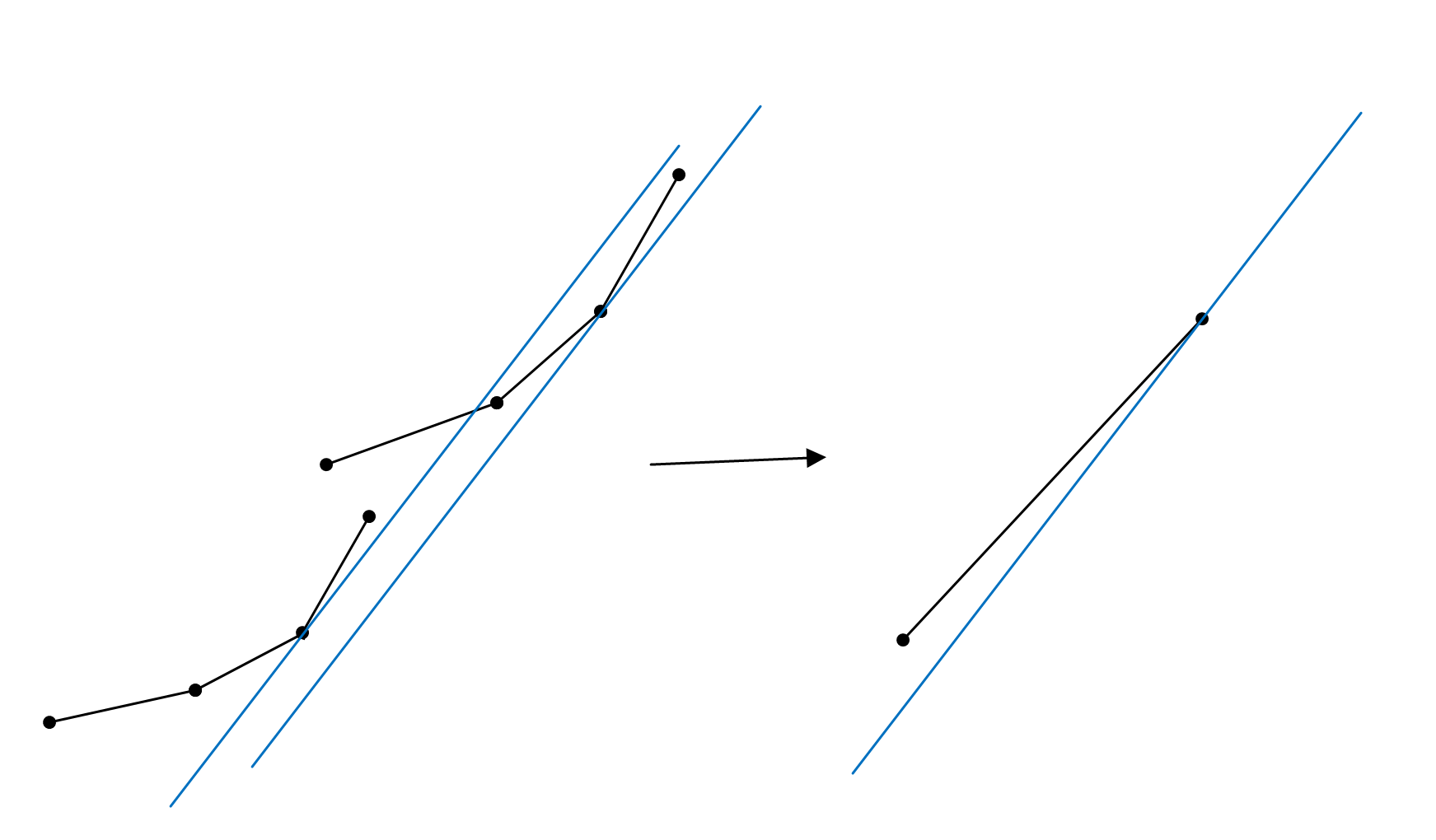
嘿!我们就可以使用线段树了!我么要开一个 $O(nlogn)$大小的线段树,线段树的结点保存对应区间的凸包(准确的说是点序列).考虑到凸包的可合并性,我相信你很快能想到如何在该线段树中寻找答案,用时应该是 $O(log^2n)$的.
我们考虑如何在线段树中插入一个结点,这并不难,我们自上到下向线段树中插入结点,但是!这是一棵树!树是有分岔的!当我们算完一条树链时,我们要返回到分岔点,在这之中,必应有结点的重新插入!如图:
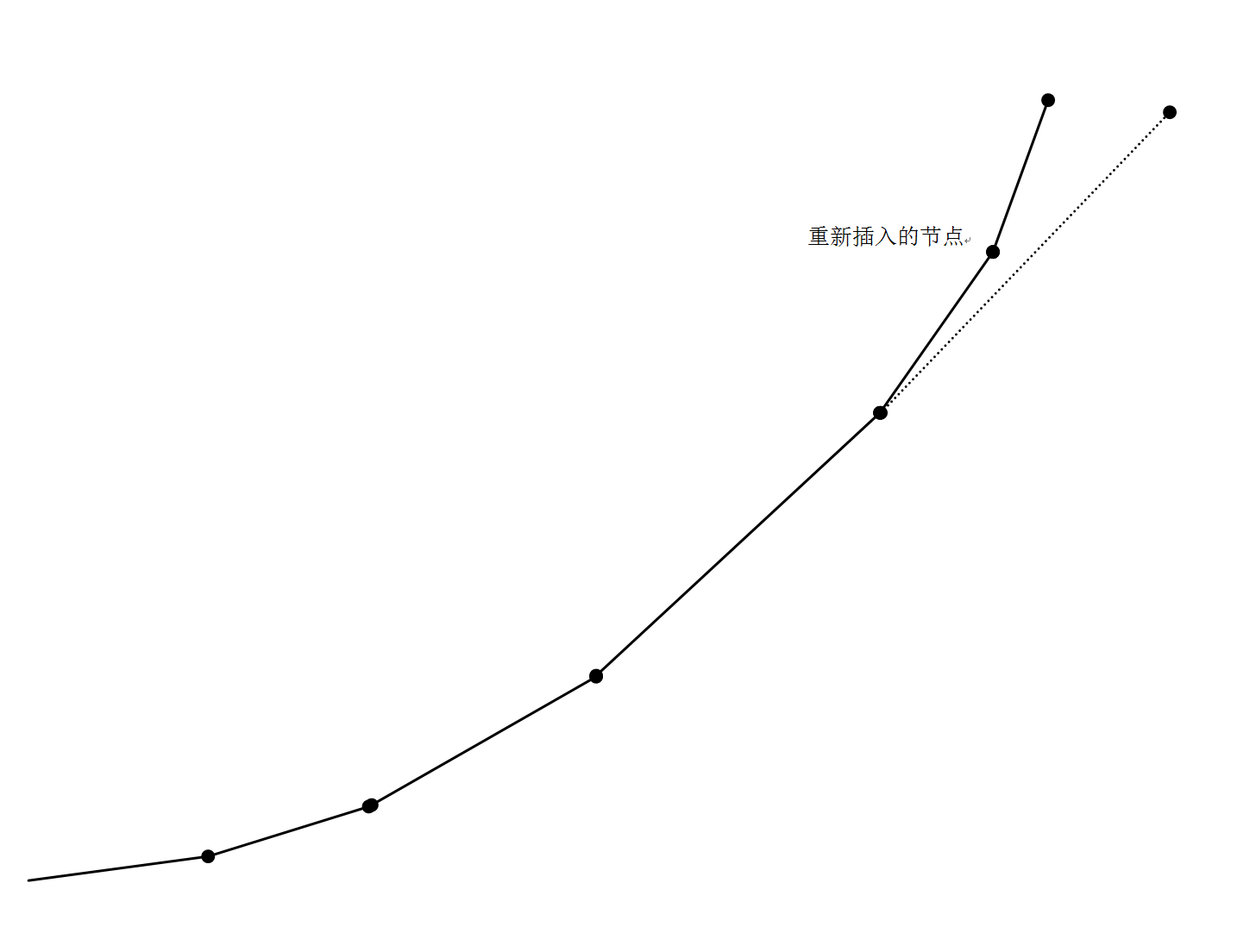
我们不可能真的将它们重新插入,那么我们在插入时就要小心,保存好插入新的结点时在线段树中覆盖的原位置数据和原凸包长度,在我们删除结点时应该将它们恢复,这样,我们每一次插入用时 $O(log^2n)$,删除用时 $O(logn)$,这对 $n<100000$已经足够了.(本人比较菜,神犇请勿吐槽)

我们回头来看我们的线段树,其实这就是可持久化线段树的一种,因为我们还要不断用到以前的版本(恢复结点).当然主席树(函数式线段树)也是可持久化线段树的一种,它由fotile主席发明,可以做到 $O(logn)$时间内求给定区间第 k <script id="MathJax-Element-4596" type="math/tex">k</script>大.