这里先总体介绍下,原文转自:
http://www.cnblogs.com/gaoxiang12/p/5560360.html
任何传感器,激光也好,视觉也好,整个SLAM系统也好,要解决的问题只有一个:如何通过数据来估计自身状态。每种传感器的测量模型不一样,它们的精度也不一样。换句话说,状态估计问题,也就是“如何最好地使用传感器数据”。可以说,SLAM是状态估计的一个特例。
1. 离散时间系统的状态估计
记机器人在各时刻的状态为
 ,其中
,其中
 是离散时间下标。在SLAM中,我们通常要估计机器人的位置,那么系统的状态就指的是机器人的位姿。用两个方程来描述状态估计问题:
是离散时间下标。在SLAM中,我们通常要估计机器人的位置,那么系统的状态就指的是机器人的位姿。用两个方程来描述状态估计问题:
解释一下变量:
 -运动方程
-运动方程
 - 输入
- 输入
 - 输入噪声
- 输入噪声
 - 观测方程
- 观测方程
 - 观测数据
- 观测数据
 - 观测噪声
- 观测噪声
运动方程描述了状态
 是怎么变到
是怎么变到
 的,而观测方程描述的是从
的,而观测方程描述的是从
 是怎么得到观察数据
是怎么得到观察数据
请注意这是一种抽象的写法。当你有实际的机器人,实际的传感器时,方程的形式就会变得具体,也就是所谓的 参数化。例如,当我们关心机器人空间位置时,可以取
![x_k = [x,y,z]_k](https://i-blog.csdnimg.cn/blog_migrate/64a34458943498d21e91e07cba1aede8.png+%3D+%5Bx%2Cy%2Cz%5D_k) 。进而,机器人携带了里程计,能够得到两个时间间隔中的相对运动,像这样
。进而,机器人携带了里程计,能够得到两个时间间隔中的相对运动,像这样

同理,观测方程也随传感器的具体信息而变。例如激光传感器可以得到空间点离机器人的距离和角度,记为
![L_k=[L_{k,x},L_{k,y}]](https://i-blog.csdnimg.cn/blog_migrate/daf06ea9735295de12e336df1ed32290.png) 是一个2D路标点。
是一个2D路标点。
举这几个例子是为了说明, 运动方程和观测方程具体形式是会变化的。但是,我们想讨论更一般的问题:当我不限制传感器的具体形式时,能否设计一种方式,从已知的
 (输入和观测数据)从,估计出
(输入和观测数据)从,估计出
 呢?
呢?
这就是最一般的状态估计问题。我们会根据
 是否线性,把它们分为
线性/非线性系统。同时,对于噪声
是否线性,把它们分为
线性/非线性系统。同时,对于噪声
 ,根据它们是否为高斯分布,分为
高斯/非高斯噪声系统。最一般的,也是最困难的问题,是非线性-非高斯(NLNG, Nonlinear-Non Gaussian)的状态估计。下面先说最简单的情况:线性高斯系统。
,根据它们是否为高斯分布,分为
高斯/非高斯噪声系统。最一般的,也是最困难的问题,是非线性-非高斯(NLNG, Nonlinear-Non Gaussian)的状态估计。下面先说最简单的情况:线性高斯系统。
2. 线性高斯系统(LG,Linear Gaussian)
在线性高斯系统中,运动方程、观测方程是线性的,且两个噪声项服从零均值的高斯分布。这是最简单的情况。简单在哪里呢?主要是因为 高斯分布经过线性变换之后仍为高斯分布。而对于一个高斯分布,只要计算出它的一阶和二阶矩,就可以描述它(高斯分布只有两个参数
 )。
)。
线性系统形式如下:
 是两个噪声项的协方差矩阵。
是两个噪声项的协方差矩阵。
 为转移矩阵和观测矩阵。
为转移矩阵和观测矩阵。
对LG系统,可以用贝叶斯法则,计算
 的后验概率分布——这条路直接通向
卡尔曼滤波器。卡尔曼是线性系统的递推形式(recursive,也就是从
的后验概率分布——这条路直接通向
卡尔曼滤波器。卡尔曼是线性系统的递推形式(recursive,也就是从
 估计
估计
 )的无偏最优估计。由于解释EKF和UKF都得用它,所以我们来推一推。如果读者不感兴趣,可以跳过公式推导环节。
)的无偏最优估计。由于解释EKF和UKF都得用它,所以我们来推一推。如果读者不感兴趣,可以跳过公式推导环节。
符号:用
 表示
表示
 的后验概率,用
的后验概率,用
![\[\tilde x\]](https://i-blog.csdnimg.cn/blog_migrate/e299873fd4eacba966723d78dd67c5d0.png) 表示它的先验概率。因为系统是线性的,噪声是高斯的,所以状态也服从高斯分布,需要计算它的均值和协方差矩阵。记第
表示它的先验概率。因为系统是线性的,噪声是高斯的,所以状态也服从高斯分布,需要计算它的均值和协方差矩阵。记第
 时刻的状态服从:
时刻的状态服从:

我们希望得到状态变量
 的最大后验估计(MAP,Maximize a Posterior),于是计算:
的最大后验估计(MAP,Maximize a Posterior),于是计算:
第二行是贝叶斯法则,第三行分母和
 无关所以去掉。
无关所以去掉。
第一项即观测方程,有:
第二项即运动方程
现在的问题是如何求解这个最大化问题。对于高斯分布,最大化问题可以变成最小化它的负对数。当我对一个高斯分布取负对数时,它的指数项变成了一个二次项,而前面的因子则变为一个无关的常数项,可以略掉(这部分我不敲了,有疑问的同学可以问)。于是,定义以下形式的最小化函数:
这个问题现在是二次项和的形式,写成矩阵形式会更加清晰。定义:
就得到矩阵形式的,类似最小二乘的问题:
于是令它的导数为零,得到:
读者会问,这个问题和卡尔曼滤波有什么问题呢?事实上, 卡尔曼滤波就是递推地求解(*)式的过程。所谓递推,就是只用
 来计算
来计算
 。对(*)进行Cholesky分解,就可以推出卡尔曼滤波器。详细过程限于篇幅就不推了,把卡尔曼的结论写一下:
。对(*)进行Cholesky分解,就可以推出卡尔曼滤波器。详细过程限于篇幅就不推了,把卡尔曼的结论写一下:
前两个是预测,第三个是卡尔曼增益,四五是校正。
另一方面,能否直接求解(*)式,得到
 呢?答案是可以的,而且这就是优化方法(batch optimization)的思路:将所有的状态放在一个向量里,进行求解。与卡尔曼滤波不同的是,在估计前面时刻的状态(如
呢?答案是可以的,而且这就是优化方法(batch optimization)的思路:将所有的状态放在一个向量里,进行求解。与卡尔曼滤波不同的是,在估计前面时刻的状态(如
一、引言
下面我们引用文献【1】中的一段话作为本文的开始:
想象你在黄昏时分看着一只小鸟飞行穿过浓密的丛林,你只能隐隐约约、断断续续地瞥见小鸟运动的闪现。你试图努力地猜测小鸟在哪里以及下一时刻它会出现在哪里,才不至于失去它的行踪。或者再想象你是二战中的一名雷达操作员,正在跟踪一个微弱的游移目标,这个目标每隔10秒钟在屏幕上闪烁一次。或者回到更远的从前,想象你是开普勒,正试图根据一组通过不规则和不准确的测量间隔得到的非常不精确的角度观测值来重新构造行星的运动轨迹。在所有这些情况下,你都试图根据随对问变化并且带有噪声的观察数据去估计物理系统的状态(例如位置、速度等等)。这个问题可以被形式化表示为时序概率模型上的推理,模型中的转移模型描述了运动的物理本质,而传感器模型则描述了测量过程。为解决这类问题,人们发展出来了一种特殊的表示方法和推理算法——卡尔曼滤波。
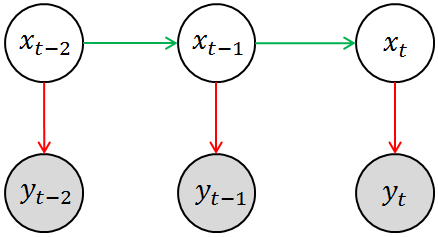
二、基本概念
回想一下HMM的基本模型(如下图所示),其中涂有阴影的圆圈(yt-2,yt-1,yt)相当于是观测变量,空白圆圈(xt-2,xt-1,xt)相当于是隐变量。这其实揭示了卡尔曼滤波与HMM之间拥有很深的渊源。回到刚刚提及的那几个例子,你所观测到的物体状态(例如雷达中目标的位置或者速度)相当于是对其真实状态的一种估计(因为观测的过程中必然存在噪声),用数学语言来表述就是P(yt | xt),这就是模型中的测量模型或测量概率(Measurement Probability)。另外一方面,物体当前的(真实)状态应该与其上一个观测状态相关,即存在这样的一个分布P(xt | xt-1),这就是模型中的转移模型或转移概率(Transition Probability)。当然,HMM中隐变量必须都是离散的,观测变量并无特殊要求。
而从信号处理的角度来讲,滤波是从混合在一起的诸多信号中提取出所需信号的过程[2]。例如,我们有一组含有噪声的行星运行轨迹,我们希望滤除其中的噪声,估计行星的真实运动轨迹,这一过程就是滤波。如果从机器学习和数据挖掘的角度来说,滤波是一个理性智能体为了把握当前状态以便进行理性决策所采取的行动[1]。比如,前两天我们没出门,但是我们可以从房间里观察路上的行人有没有打伞(观测状态)来估计前两天有没有下雨(真实状态)。基于这些情况,现在我们要来决策今天(是否会有雨以及)外出是否需要打伞,这个过程就是滤波。读者应该注意把握上面两个定义的统一性。
所谓估计就是根据测量得出的与状态X(t) 有关的数据Y(t) = h[X(t)] + V(t) 解算出X(t)的计算值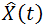
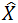
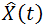
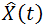
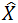
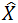
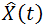
- 当t = t1 时,
称为X(t)的估计;
- 当t > t1 肘,
称为X(t)的预测;
- 当t < t1 时,
称为X(t)的平滑。
最优估计是指某一指标函数达到最值时的估计。卡尔曼滤波就是一种线性最优滤波器。
因为后面会用到,这里我们补充一下关于协方差矩阵的概念。
设 n 维随机变量(X1,X2, …,Xn)的2阶混合中心距
σij= cov(Xi,Xj) = E[(Xi-E(Xi))(Xj-E(Xj))], (i,j = 1, 2, …, n)
都存在,则称矩阵
为 n 维随机变量(X1,X2, …,Xn)的协方差矩阵,协方差矩阵是一个对称矩阵,而且对角线是各个维度的方差。
维基百科中还给出了协方差矩阵的一些重要性质,例如下面这两条(此处不做具体证明)。后续的内容会用到其中的第一条。
三、卡尔曼滤波的方程推导
直接从数学公式和概念入手来考虑卡尔曼滤波无疑是一件非常枯燥的事情。为了便于理解,我们仍然从一个现实中的实例开始下面的介绍,这一过程中你所需的预备知识仅仅是高中程度的物理学内容。
假如现在有一辆在路上做直线运动的小车(如下所示),该小车在 t 时刻的状态可以用一个向量来表示,其中pt 表示他当前的位置,vt表示该车当前的速度。当然,司机还可以踩油门或者刹车来给车一个加速度ut,ut相当于是一个对车的控制量。显然,如果司机既没有踩油门也没有踩刹车,那么ut就等于0。此时车就会做匀速直线运动。
如果我们已知上一时刻 t-1时小车的状态,现在来考虑当前时刻t 小车的状态。显然有
易知,上述两个公式中,输出变量都是输入变量的线性组合,这也就是称卡尔曼滤波器为线性滤波器的原因所在。既然上述公式表征了一种线性关系,那么我们就可以用一个矩阵来表示它,则有
如果另其中的
则得到卡尔曼滤波方程组中的第一条公式——状态预测公式,而F就是状态转移矩阵,它表示我们如何从上一状态来推测当前状态。而B则是控制矩阵,它表示控制量u如何作用于当前状态。
(1)
上式中x顶上的hat表示为估计值(而非真实值)。等式左端部分的右上标“-”表示该状态是根据上一状态推测而来的,稍后我们还将对其进行修正以得到最优估计,彼时才可以将“-”去掉。
既然我们是在对真实值进行估计,那么就理应考虑到噪声的影响。实践中,我们通常都是假设噪声服从一个0均值的高斯分布,即Noise~Guassian(0,σ)。例如对于一个一维的数据进行估计时,若要引入噪声的影响,其实只要考虑其中的方差σ即可。当我们将维度提高之后,为了综合考虑各个维度偏离其均值的程度,就需要引入协方差矩阵。
回到我们的例子,系统中每一个时刻的不确定性都是通过协方差矩阵 Σ 来给出的。而且这种不确定性在每个时刻间还会进行传递。也就是说不仅当前物体的状态(例如位置或者速度)是会(在每个时刻间)进行传递的,而且物体状态的不确定性也是会(在每个时刻间)进行传递的。这种不确定性的传递就可以用状态转移矩阵来表示,即(注意,这里用到了前面给出的关于协方差矩阵的性质)
但是我们还应该考虑到,预测模型本身也并不绝对准确的,所以我们要引入一个协方差矩阵 Q 来表示预测模型本身的噪声(也即是噪声在传递过程中的不确定性),则有
(2)
这就是卡尔曼滤波方程组中的第二条公式,它表示不确定性在各个时刻间的传递关系。
继续我们的小汽车例子。你应该注意到,前面我们所讨论的内容都是围绕小汽车的真实状态展开的。而真实状态我们其实是无法得知的,我们只能通过观测值来对真实值进行估计。所以现在我们在路上布设了一个装置来测定小汽车的位置,观测到的值记为V(t)。而且从小汽车的真实状态到其观测状态还有一个变换关系,这个变换关系我们记为h(•),而且这个h(•)还是一个线性函数。此时便有(该式前面曾经给出过)
Y(t) = h[X(t)] + V(t)
其中V(t)表示观测的误差。既然h(•)还是一个线性函数,所以我们同样可以把上式改写成矩阵的形式,则有
Yt=Hxt + v
就本例而言,观测矩阵 H = [1 0],这其实告诉我们x和Z的维度不一定非得相同。在我们的例子中,x是一个二维的列向量,而Z只是一个标量。此时当把x与上面给出的H相乘就会得出一个标量,此时得到的Y 就是x中的首个元素,也就是小车的位置。同样,我们还需要用一个协方差矩阵R来取代上述式子中的v来表示观测中的不确定性。当然,由于Z是一个一维的值,所以此时协方差矩阵R也只有一维,也就是只有一个值,即观测噪声之高斯分布的参数σ。如果我们有很多装置来测量小汽车的不同状态,那么Z就会是一个包含所有观测值的向量。
接下来要做的事情就是对前面得出的状态估计进行修正,具体而言就是利用下面这个式子
直观上来说,上式并不难理解。前面我们提到,是根据上一状态推测而来的,那么它与“最优”估计值之间的差距现在就是等式右端加号右侧的部分。
表示实际观察值与预估的观测值之间的残差。这个残差再乘以一个系数K就可以用来对估计值进行修正。K称为卡尔曼系数,它也是一个矩阵,它是对残差的加权矩阵,有的资料上称其为滤波增益阵。
(3)
上式的推导比较复杂,有兴趣深入研究的读者可以参阅文献【2】(P35~P37)。如果有时间我会在后面再做详细推导。但是现在我们仍然可以定性地对这个系数进行解读:滤波增益阵首先权衡预测状态协方差矩阵Σ 和观测值矩阵R的大小,并以此来觉得我们是更倾向于相信预测模型还是详细观测模型。如果相信预测模型多一点,那么这个残差的权重就会小一点。反之亦然,如果相信观察模型多一点,这个残差的权重就会大一点。不仅如此,滤波增益阵还负责把残差的表现形式从观测域转换到了状态域。例如本题中观测值Z 仅仅是一个一维的向量,状态 x 是一个二维的向量。所以在实际应用中,观测值与状态值所采用的描述特征或者单位都有可能不同,显然直接用观测值的残差去更新状态值是不合理的。而利用卡尔曼系数,我们就可以完成这种转换。例如,在小车运动这个例子中,我们只观察到了汽车的位置,但K里面已经包含了协方差矩阵P的信息(P里面就给出了速度和位置的相关性),所以它利用速度和位置这两个维度的相关性,从位置的残差中推算出了速度的残差。从而让我们可以对状态值 x 的两个维度同时进行修正。
最后,还需对最优估计值的噪声分布进行更新。所使用的公式为
(5)
至此,我们便获得了实现卡尔曼滤波所需的全部五个公式,我在前面分别用(1)~(5)的标记进行了编号。我现在把它们再次罗列出来:
我们将这五个公式分成预测组和更新组。预测组总是根据前一个状态来估计当前状态。更新组则根据观测信息来对预测信息进行修正,以期达到最优估计之目的。
四、一个简单的实例
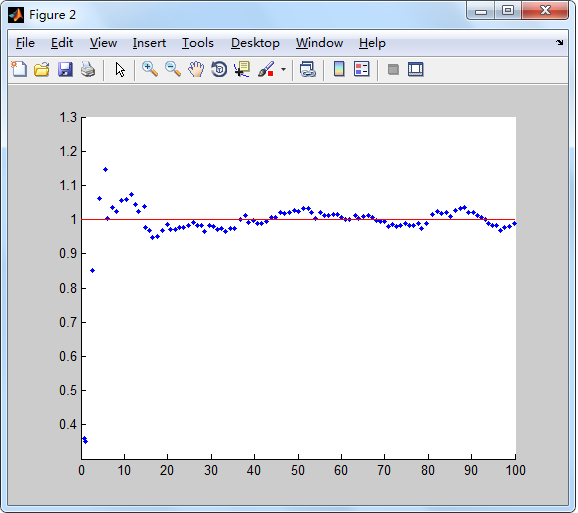
当然,你可能困惑于卡尔曼滤波是否真的有效。下面利用文献[4]中给出的例子(为提升显示效果,笔者略有修改)来演示卡尔曼滤波的威力。这个例子模拟质点进行匀速直线运动(速度为1),然后引入一个非常大的噪声,再用卡尔曼滤波来对质点的运动状态进行轨迹。注意是匀速直线运动,所以其中不含有控制变量。
- Z=(1:100); %观测值
- noise=randn(1,100); %方差为1的高斯噪声
- Z=Z+noise;
- X=[0; 0]; %状态
- Sigma = [1 0; 0 1]; %状态协方差矩阵
- F=[1 1; 0 1]; %状态转移矩阵
- Q=[0.0001, 0; 0 0.0001]; %状态转移协方差矩阵
- H=[1 0]; %观测矩阵
- R=1; %观测噪声方差
- figure;
- hold on;
- for i=1:100
- X_ = F*X;
- Sigma_ = F*Sigma*F'+Q;
- K = Sigma_*H'/(H*Sigma_*H'+R);
- X = X_+K*(Z(i)-H*X_);
- Sigma = (eye(2)-K*H)*Sigma_;
- plot(X(1), X(2), '.','MarkerSize',10); %画点,横轴表示位置,纵轴表示速度
- end
- plot([0,100],[1,1],'r-');
Z=(1:100); %观测值
noise=randn(1,100); %方差为1的高斯噪声
Z=Z+noise;
X=[0; 0]; %状态
Sigma = [1 0; 0 1]; %状态协方差矩阵
F=[1 1; 0 1]; %状态转移矩阵
Q=[0.0001, 0; 0 0.0001]; %状态转移协方差矩阵
H=[1 0]; %观测矩阵
R=1; %观测噪声方差
figure;
hold on;
for i=1:100
X_ = F*X;
Sigma_ = F*Sigma*F'+Q;
K = Sigma_*H'/(H*Sigma_*H'+R);
X = X_+K*(Z(i)-H*X_);
Sigma = (eye(2)-K*H)*Sigma_;
plot(X(1), X(2), '.','MarkerSize',10); %画点,横轴表示位置,纵轴表示速度
end
plot([0,100],[1,1],'r-'); 下图给出了上述代码的执行结果。可见经过最开始的几次迭代后,质点运动的状态估计就回到了正确轨迹上,而且估计的结果基本围绕在真实值附近,效果还是很理想的。
五、后记
本文相当于是卡尔曼滤波的入门文,在下一篇中我将深入挖掘一些本文未曾提及的细节(以及一些本文没有给出的数学上的推导)。如果你想将自己对卡尔曼滤波的认识提升到一个更高的档次,推荐你关注我的后续博文。Cheers~
如果你是图像处理的同道中人,欢迎加入图像处理学习群(529549320)。为保证本群质量,入群前请先阅读群规(即本博客置顶文章),并在博客置顶帖中留言,否则将不予入群。Cheers~
参考文献:
【1】Stuart Russell and Peter Norvig. Artificial Intelligence: A Modern Approach. 3rd Edition.
【2】秦永元,张洪钺,汪叔华,卡尔曼滤波与组合导航原理,西北工业大学出版社
【3】徐亦达博士关于卡尔曼滤波的公开课,http://v.youku.com/v_show/id_XMTM2ODU1MzMzMg.html
【4】卡尔曼滤波的原理以及在MATLAB中的实现,http://blog.csdn.net/revolver/article/details/37830675
3. 扩展卡尔曼滤波器
一件悲剧的事情是: 高斯分布经过非线性变换后,不再是高斯分布。而且,是个什么分布,基本说不上来。(摊手)
如果没有高斯分布,上面说的那些都不再成立了。 于是EKF说,嘛,我们睁一只眼闭一只眼,用高斯分布去近似它,并且,在工作点附近对系统进行线性化。当然这个近似是很成问题的,有什么问题我们之后再说。
EKF的做法主要有两点。其一,在工作点附近
这里的几个偏导数,都在工作点处取值。于是呢,它就被 活生生地当成了一个线性系统。
第二,在线性系统近似下,把噪声项和状态都 当成了高斯分布。这样,只要估计它们的均值和协方差矩阵,就可以描述状态了。经过这样的近似之后呢,后续工作都和卡尔曼滤波是一样的了。所以EKF是卡尔曼滤波在NLNG系统下的直接扩展(所以叫扩展卡尔曼嘛)。EKF给出的公式和卡尔曼是一致的,用线性化之后的矩阵去代替卡尔曼滤波器里的转移矩阵和观测矩阵即可。
这样做听起来还是挺有道理的,实际上也是能用的,但是问题还是很多的。
考虑一个服从高斯分布的变量
 ,现在
,现在
 ,问
,问
 服从什么分布?
服从什么分布?
我概率比较差,不过这个似乎是叫做卡尔方布。
 应该是下图中k=1那条线。
应该是下图中k=1那条线。
 。假设我们采样时得到了一个
。假设我们采样时得到了一个
 ,那么就会近似成一个均值为0.25的高斯分布,然而卡方分布的期望应该是1。……但是各位真觉得k=1那条线像哪个高斯分布吗?
,那么就会近似成一个均值为0.25的高斯分布,然而卡方分布的期望应该是1。……但是各位真觉得k=1那条线像哪个高斯分布吗?
所以EKF面临的一个重要问题是,当一个高斯分布经过非线性变换后,如何用另一个高斯分布近似它?按照它现在的做法,存在以下的局限性:(注意是滤波器自己的局限性,还没谈在SLAM问题里的局限性)。
- 即使是高斯分布,经过一个非线性变换后也不是高斯分布。EKF只计算均值与协方差,是在用高斯近似这个非线性变换后的结果。(实际中这个近似可能很差)。
- 系统本身线性化过程中,丢掉了高阶项。
- 线性化的工作点往往不是输入状态真实的均值,而是一个估计的均值。于是,在这个工作点下计算的
 ,也不是最好的。
,也不是最好的。 - 在估计非线性输出的均值时,EKF算的是
 的形式。这个结果几乎不会是输出分布的真正期望值。协方差也是同理。
的形式。这个结果几乎不会是输出分布的真正期望值。协方差也是同理。
- 为了克服第3条工作点的问题,我们以EKF估计的结果为工作点,重新计算一遍EKF,直到这个工作点变化够小。是为迭代EKF(Iterated EKF, IEKF)。
- 为了克服第4条,我们除了计算
 ,再计算其他几个精心挑选的采样点,然后用这几个点估计输出的高斯分布。是为Sigma Point KF(SPKF,或UKF)。
,再计算其他几个精心挑选的采样点,然后用这几个点估计输出的高斯分布。是为Sigma Point KF(SPKF,或UKF)。
如果不那么乖,可以说:我们不要高斯分布假设,凭什么要用高斯去近似一个长得根本不高斯的分布呢?于是问题变为,丢掉高斯假设后,怎么描述输出函数的分布就成了一个问题。一种比较暴力的方式是:用足够多的采样点,来表达输出的分布。这种蒙特卡洛的方式,也就是粒子滤波的思路。
如果再进一步,可以丢弃滤波器思路,说:为什么要用前一个时刻的值来估计下一个时刻呢?我们可以把所有状态看成变量,把运动方程和观测方程看成变量间的约束,构造误差函数,然后最小化这个误差的二次型。这样就会得到非线性优化的方法,在SLAM里就走向图优化那条路上去了。不过,非线性优化也需要对误差函数不断地求梯度,并根据梯度方向迭代,因而局部线性化是不可避免的。
可以看到,在这个过程中,我们逐渐放宽了假设。
再给一篇EKF的文章:原文:
http://www.cnblogs.com/ymxiansen/p/5368547.html
已经历经了半个世纪的卡尔曼滤波至今仍然是研究的热点,相关的文章不断被发表。其中许多文章是关于卡尔曼滤波器的新应用,但也不乏改善和扩展滤波器算法的研究。而对算法的研究多着重于将卡尔曼滤波应用于非线性系统。
为什么学界要这么热衷于将卡尔曼滤波器用于非线性系统呢?因为卡尔曼滤波器从一开始就是为线性系统设计的算法,不能用于非线性系统中。但是事实上多数系统都是非线性的,所以如果卡尔曼滤波器不能用在非线性系统中的话,那么它的应用范围就非常有限了。如果真的是这样,卡尔曼滤波器可能早就寿终正寝或者过很久很久才会被人注意到。幸运的是早期的学者们对这个问题理解的非常深刻,而且也找到了解决方法,就是扩展卡尔曼滤波(EKF)。
事实上世界上的第一个卡尔曼滤波也是扩展卡尔曼滤波,而不是线性卡尔曼滤波器。扩展卡尔曼滤波有很久远的历史,如果说有一个非线性系统需要用到卡尔曼滤波的话,不必怀疑,先试试扩展卡尔曼滤波准没错。因为他有很久远的历史,所以可以轻松的找到许多这方面的资料。
不过扩展卡尔曼滤波也不是无懈可击的,它有一个很严重的短板——发散。使用扩展卡尔曼滤波的时候请务必记在心上,时刻提醒自己,这样设计滤波器其结果会发散吗?毫不夸张地说相对于线性卡尔曼滤波设计扩展卡尔曼滤波器的就是在解决发散问题。发散问题解决了剩下的都是小事。
小结:
- 扩展卡尔曼滤波器主要用于非线性系统;
- 扩展卡尔曼滤波器会发散。
线性化的卡尔曼滤波器
在讨论扩展卡尔曼滤波之前,首先要了解一下线性化卡尔曼滤波。它和线性卡尔曼滤波器在滤波器的算法方面有同样的算法结构,一样一样的。不一样的地方在于这两者的系统模型不同。线性卡尔曼滤波器的系统本身就是线性系统,而线性化卡尔曼滤波器的系统本身是非线性系统,但是机智的大神们将非线性的系统进行了线性化,于是卡尔曼滤波就可以用在非线性系统中了。对于一个卡尔曼滤波器的设计者,就不要去管你的模型到底是一开始就是线性系统还是非线性系统线性化得到的线性系统,反正只要是线性系统就好了。好了,现在你有了一个线性系统,那你还需要担心什么呢?这就是一个之前讲过的线性卡尔曼滤波器啦。
的确是这样的,没有很大的差别,但是请跟我一起念:线性化卡尔曼滤波器会发散。为什么会发散呢?是这样,我们在对非线性系统进行线性化的过程中,只有被线性化的那个点附近的线性化模型和真实的模型相近,远的误差就大了,那么这个时候卡尔曼滤波器的效果就不好。如果懂点线性化知识这个道理就很明显。所以线性化的这个限制要时刻考虑,这也就是为什么要把线性卡尔曼滤波器和线性化卡尔曼滤波器区分开的理由。
而决定一个线性化滤波器成功与否的关键就在于这个滤波器系统模型线性化得好不好。一个贴近于真实模型的线性化模型对于滤波器的良好输出非常重要。所以说掌握如何线性化一个非线性模型很重要,然而我们并不会讨论关于系统线性化的问题,因为这已经不属于卡尔曼滤波的范畴了,而且每个系统有不同的线性化方法,有点复杂。
总而言之,如果你已经明白了如何使用线性卡尔曼滤波器,那么使用线性化卡尔曼滤波器就没有什么需要担心的,因为算法结构一样嘛。唯一需要注意的就是线性化卡尔曼滤波器会发散,要在有效范围内使用,要不然滤波器的表现不会好。
小结:
- 线性化卡尔曼滤波器与线性卡尔曼滤波器有同样的算法结构,不同样的系统模型;
- 线性化卡尔曼滤波器会发散,原因在于函数在远于被线性化的点的时候并不接近于非线性函数;
- 线性化卡尔曼的表现取决于线性化做得好不好。
扩展卡尔曼滤波器
在这节具体介绍卡尔曼滤波器。首先从比较熟悉的线性卡尔曼滤波器开始比较扩展卡尔曼滤波器与线性化卡尔曼滤波器的异同,从系统模型到滤波器算法,并解释这些不同。之后将提供两个具体的应用例子来加以体会。这门书的重点在于如何感性的理解和使用卡尔曼滤波器,所以对于算法的推导不会被具体描述。但是如何理解和区别这些不同,这些不同表达了什么意义将会一一解释。如下图所示,右面是我们已经熟悉的经典的线性化卡尔曼滤波的算法结构和步骤,左面则是扩展卡尔曼滤波器的算法结构和步骤,其中不同的地方已经用红笔圈出来。可以看到两个滤波器的算法结构是相同的,只有几个方程上有细微的差别。

非线性系统模型
在非线性系统中,系统模型是这样的:
xk+1 = f(Xk)+ wk
zk = h(Xk) + vk
这与线性系统的区别在于非线性系统的状态向量和其系数是不能够分离的。
比如说,在GPS定位的伪距与接收机位置的关系中:ρ[Xu]= [(xu-xsi)2 + (yu -ysi)2 +(zu - zsi)2 ]1/2 + b + vi ,
其中[Xu]=[xu,yu,zu,b]是系统状态向量,分别是接收机的位置和接收机与卫星的钟差,
[xsi,ysi,zsi]是卫星的位置坐标,ρ是伪距,vi是观测噪声。
在这个关系中状态向量与它的系数就是不可分离的,没有办法写成AXk的形式,只能是f(Xk)。h(Xk)的存在同理。
扩展卡尔曼滤波器算法
比较上图,可以看到差别主要在这样两个地方:
- 第 I 步中xk+1 = f(xk-1),与原来的xk+1 = Axk-1;
- 第 III 步中Xk = Xk- + Kk(zk - h(xk-)),与原来的Xk = Xk- + Kk(zk - Hxk-);
其他的地方则完全一样。那么是不是只需要改动这两点就可以将一个线性卡尔曼滤波变成扩展卡尔曼滤波呢?不是的,有一些更重要的差别隐藏在公式中。在右图中,也就是线性卡尔曼滤波器中矩阵A和矩阵H是已知的,在而左图中虽然将第I步和第III步中的A和H替换成f和h,但是其他地方的A和H却仍然存在,可是在非线性系统中,哪有A和H呢?
A和H的获得就要涉及到之前所提到的决定扩展卡尔曼滤波器表现的决定因素:线性化。线性化的方法很经典:
将非线性系统中的f对x求(xk估计)处的偏导得到A,同样的求h对x求(xk-)处的偏导得到H。(向量和矩阵怎么求偏导?)
线性化滤波器和扩展卡尔曼滤波器的共同点在于他们都需要经历一个线性化的过程,不同点在于,扩展卡尔曼滤波器是将xk估计作为线性化的参考点,线性化卡尔曼滤波器不是。(线性化滤波器是用什么作为线性化参考点?参考点是不是就是求偏导以后的带入值?) 在设计扩展卡尔曼滤波器的时候是不是知道这一点并不会有什么不同。但是如果你在犹豫我是要用扩展卡尔曼滤波器还是用线性化卡尔曼滤波器的时候,明白这一点是非常重要的。下面对线性化滤波器和卡尔曼滤波器线性化参考点的差异做简单的解释。
在扩展卡尔曼滤波中,我们并不用前一个时刻的先验值Xk-(卡尔曼滤波器未经过修正的预测值)作为参考点,而是用前一个时刻的估计值作为参考点做线性化。这是因为相对于先验值,前一个时刻的估计值更加贴近于真实值,将估计值作为线性化参考点可以得到一个更加贴近于实际的线性化系统模型。这种线性化方法跟适合难以提前确定线性化参考点的系统模型。而相反的。如果说线性化参考点已经确定了,那么完全不必用前一刻的估计值作为线性化参考点。比如说在对卫星的位置这样的系统模型进行线性化的时候,由于卫星的运动轨迹有一个连续的轨道,在这种情况下,就不必用前一个时刻的估计值作为线性化参考点。(而是直接用系统对下一个时刻的预测就可以了?)
总而言之,你只要有个概念,扩展卡尔曼滤波器是基于先验估计做系统线性化的就可以了。具体的细节在实验中就会有所体会。重要的是我们知道了A和H是根据上面两个公式得到的。
总结一下这一小结讲的什么。我们看到总体而言扩展卡尔曼滤波器的结构过程都和线性卡尔曼滤波器相同。但是每一步的等式都有一些细微的差别,这些差别可以分为两块:第一个是扩展卡尔曼滤波器用非线性系统系统方程f和h替换了线性系统的A和H。第二个是扩展卡尔曼滤波器中的矩阵A和矩阵H是非线性系统的雅可比行列式(什么鬼)。除了这两块剩下的都和线性卡尔曼滤波器相同。
小结:
- 在第I步和第III步中,用f和h代替原来的A和H;
- 剩下的A和H,分别求f和h在(xk估计)和(xk-)处的偏导得到;
- 扩展卡尔曼滤波器用前一个时刻的估计值作为参考点做线性化。
总结:
所谓扩展卡尔曼滤波器,就是适用于非线性系统的卡尔曼滤波器。它与经典的线性卡尔曼滤波器很相似,算法步骤和结构都相同。不同在于系统模型和矩阵A和H。在扩展卡尔曼滤波器当中用非线性系统模型方程代替线性系统墨香的系统方程;将系统模型求偏导得到新的扩展卡尔曼滤波器当中的矩阵A和H,在偏导的求解过程中,也是就是线性化的过程中用前一个时刻的估计值作为参考点。通过这样的修改就得到了适用于非线性系统的扩展卡尔曼滤波器。在使用的过程中我们要时刻牢记,扩展卡尔曼滤波会发散。下一篇是实验。
未解决的问题:1.如何对非线性系统线性化,求偏导就可以吗?2.矩阵和向量怎么求偏导?3.为什么f和h求偏导的点不同?4.线性化参考点是不是就是求偏导以后的参考点?5.雅可比行列式?
4. UKF 无迹卡尔曼
由于题主问题里没谈IEKF,我们就简单说说UKF和PF。UKF主要解决一个高斯分布经过非线性变换后,怎么用另一个高斯分布近似它。假设
 ,我们希望用
,我们希望用
 近似
近似
 。按照EKF,需要对
。按照EKF,需要对
 做线性化。但在UKF里,不必做这个线性化。
做线性化。但在UKF里,不必做这个线性化。
UKF的做法是找一些叫做Sigma Point的点,把这些点用
 投影过去。然后,用投影之后的点做出一个高斯分布,如下图:
投影过去。然后,用投影之后的点做出一个高斯分布,如下图:
- 不必线性化,也不必求导,对
 没有光滑性要求。
没有光滑性要求。 - 计算量随维数增长是线性的。
5. PF 粒子滤波
UKF的一个问题是输出仍假设成高斯分布。然而,即使在很简单的情况下,高斯的非线性变换仍然不是高斯。并且,仅在很少的情况下,输出的分布有个名字(比如卡方),多数时候你都不知道他们是啥……更别提描述它们了。因为描述很困难,所以粒子滤波器采用了一种暴力的,用大量采样点去描述这个分布的方法(老子就是无参的你来打我呀)。框架大概像下面这个样子,就是一个不断采样——算权重——重采样的过程:
这种采样思路的最大问题是: 采样所需的粒子数量,随分布是指数增长的。所以仅限于低维的问题,高维的基本就没办法了。
6. 非线性优化
非线性优化,计算的也是最大后验概率估计(MAP),但它的处理方式与滤波器不同。对于上面写的状态估计问题,可以简单地构造误差项:这里仅用到了噪声项满足高斯分布的假设,再没有更多的了。当构建一个非线性优化问题之后,就可以从一个初始值出发,计算梯度(或二阶梯度),优化这个目标函数。常见的梯度下降策略有牛顿法、高斯-牛顿法、Levenberg-Marquardt方法,可以在许多讲数值优化的书里找到。
非线性优化方法现在已经成为视觉SLAM里的主流,尤其是在它的稀疏性质被人发现且利用起来之后。它与滤波器最大不同点在于, 一次可以考虑整条轨迹中的约束。它的线性化,即雅可比矩阵的计算,也是相对于整条轨迹的。相比之下,滤波器还是停留在马尔可夫的假设之下,只用上一次估计的状态计算当前的状态。可以用一个图来表达它们之间的关系:
7. 小结
- 卡尔曼滤波是递归的线性高斯系统最优估计。
- EKF将NLNG系统在工作点附近近似为LG进行处理。
- IEKF对工作点进行迭代。
- UKF没有线性化近似,而是把sigma point进行非线性变换后再用高斯近似。
- PF去掉高斯假设,以粒子作为采样点来描述分布。
- 优化方式同时考虑所有帧间约束,迭代线性化求解








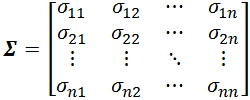
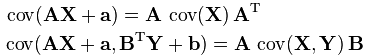

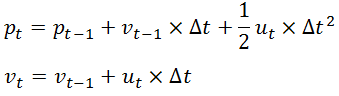
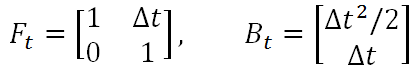



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








