优化：等式约束

优化：等式约束1

问题描述：

等式约束：

$$\begin{equation} {\rm minimize} \quad f({\bf x}) \\ {\rm subject \ to} \quad {\bf h}({\bf x})={\bf 0} \end{equation}$$
其中， $\bf x \in \mathbb R^n$， $f: \mathbb R^n \rightarrow \mathbb R$， $\bf h: \mathbb R^n \rightarrow \mathbb R^m$， $\bf h=[h_1, ..., h_m]^T$，并且 $m\le n$。 $\bf h$是连续可微的。

一些定义

• regular point
  

  A point ${\bf x}^*$ satisfying the constraints $h_1({\bf x}^*)=0,...,h_m({\bf x}^*)=0$ is said to be a regular point of the constraints if the gradient vectors $\nabla h_1({\bf x}^*),...,\nabla h_m({\bf x}^*)$ are linearly independent.

• tangent space
  The tangent space at a point ${\bf x}^*$ on the surface $S=\{{\bf x} \in {\mathbb R}^n:{\bf h}({\bf x})={\bf 0}\}$ is the set $T({\bf x}^*)=\{ {\bf y}: D{\bf h}({\bf x}^*){\bf y}={\bf 0}\}$

• normal space

  The normal space at a point ${\bf x}^*$ on the surface $S=\{{\bf x} \in {\mathbb R}^n:\bf h({\bf x})={\bf 0}\}$ is the set $N({\bf x}^*)=\{ {\bf x} \in {\mathbb R}^n:{\bf x}= D{\bf h}({\bf x}^*)^Tz,z\in \mathbb R^m\}$

• 定理

  $T({\bf x}^*)=N({\bf x}^*)^\bot$ and $T({\bf x}^*)^\bot = N({\bf x}^*)$

拉格朗日条件

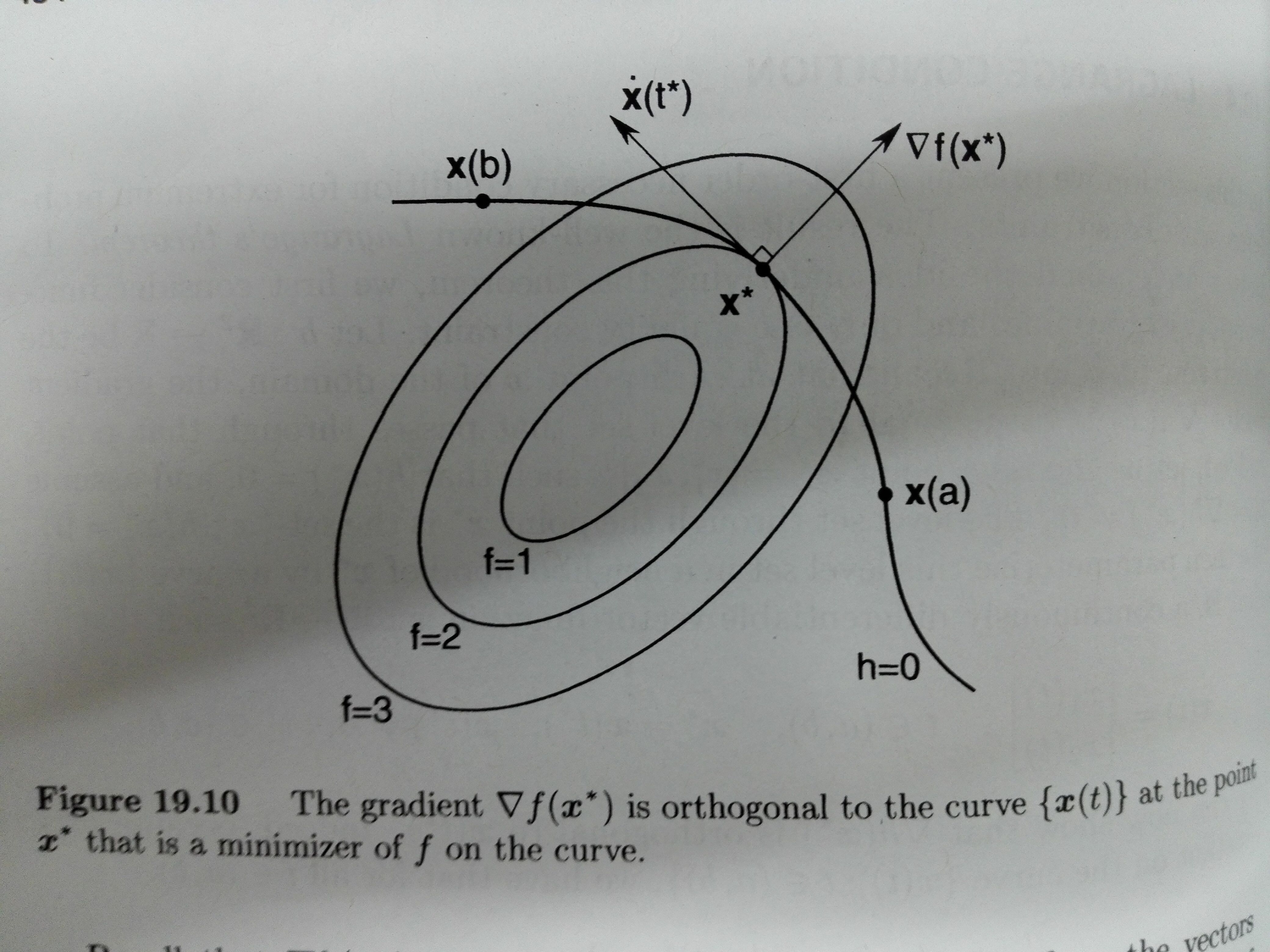
拉格朗日条件图解[1]：

• 
  
• 拉格朗日定理
  

Let ${\bf x}^*$ be a local minimizer (or maximizer) of $f:{\mathbb R}^n \rightarrow {\mathbb R}$, subject to ${\bf h}({\bf x})={\bf 0}$, ${\bf h}:{\mathbb R}^n \rightarrow {\mathbb R}^m, m<n$. Assume that ${\bf x}^*$ is a regular point. Then, there exists $\bf \lambda \in \mathbb R^m$ such that
$$Df({\bf x}^*)+{\bf \lambda}^{*{\mathrm T}} D{\bf h}({\bf x}^*)={\bf 0}^T$$ .

• Example
  考虑下述问题
  $$\rm maximize \frac{\bf x^\mathrm T Q \bf x}{\bf x^\mathrm T P \bf x}$$
  求解思路：
  用拉格朗日法求解，但是没有等式约束。通过观察发现，如果对$\bf x$扩大一定倍数，如$t$，那么$t\bf x$的解与$\bf x$的相同，所以我们可以将$\bf x^\mathrm T P \bf x$约束为1，所以原问题变成
  $$\begin{equation} {\rm maximize} \quad {\bf x}^{\mathrm T} {\bf Q} {\bf x} \\ {\rm subject \ to}\quad {\bf x}^{\mathrm T} {\bf P} {\bf x} = 1. \end{equation}$$
  便可以用拉格朗日法求解。

二次条件

上面所说的拉格朗日法是针对函数的一阶导的，下面就二阶导进行讨论。
记$\bf L(\bf x, \lambda)$是拉格朗日方程的Hessian矩阵：

$${\bf L}({\bf x}, \lambda)={\bf F}({\bf x})+\lambda_1 {\bf H}_1({\bf x})+....+\lambda_m {\bf H}_m({\bf x})$$
给出结论：

• 定理

  Suppose that $f, {\bf h} \in {\mathcal C}^2$ and there exits a point ${\bf x}^* \in {\mathbb R}^n$ and ${\bf \lambda}^* \in {\mathbb R}^m$ such that:

  1. $Df({\bf x}^*)+\bf \lambda^{* \rm T} \rm D \bf h({\bf x}^*)=\bf 0^\rm T$ .
  2. For all ${\bf y} \in T({\bf x}^*), {\bf y}\neq {\bf 0}$, we have ${\bf y}^{\rm T} {\bf L}({\bf x}^*, \lambda^*){\bf y}>0$.
     Then, ${\bf x}^*$ is a strict local minimizer of $f$ subject to ${\bf h}({\bf x})={\bf 0}$.

  对于局部最大值也是同样的条件约束，区别在于第二项中的正定变成了负定。

[1]图片来自《AN INTRODUCTION TO OPTIMIZATION》P434

---

1. 参考《AN INTRODUCTION TO OPTIMIZATION》和《CONVEX OPTIMIZATION》. ↩