前两篇博客介绍了ML中的一些基本概念,还有一些很重要的概念也还没有说到,作为入门教程还是需要直观点,所以先举个最简单的例子线性回归(linear regresion),接下来引出后续的概念.
从线性回归说起
线性回归很简单,给定一定的输入X,输出相应的输出Y,输出是输入的线性函数.这里使用Andrew Ng ML课程中的线性回归的例子,假设是单变量的linear regression.
这里有一些约定,以后我们也使用这些约定:
此时我们的假设是:
这里的theta表示叫做参数(parameters),或者叫做权重(weight):
Parameters(weights) are values that control the behavior of the system and determine how each feature affects the prediction.
如果使用MSE(Mean Squared Error)误差的话,此时的cost function(objective function)是:
现在要做的就是minimize cost function,数学上直接求梯度(gradient)为0的点就可以了.
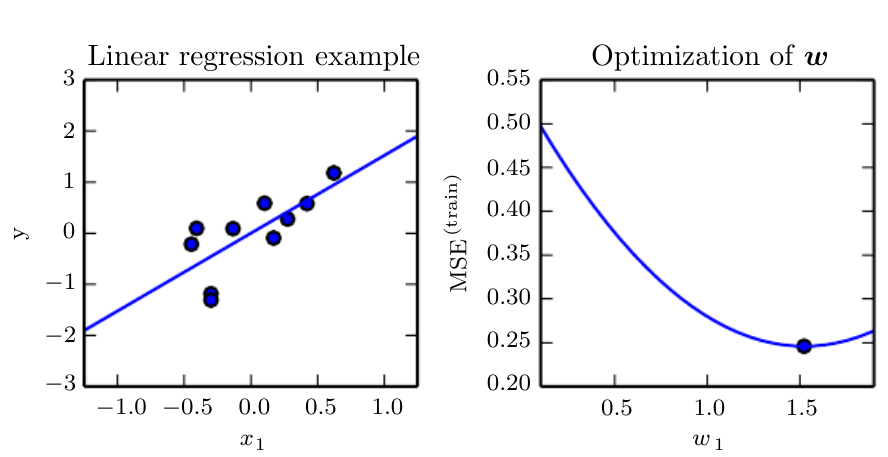
现在假设有10个数据点,做出图来大概是下面这样(把W当做是theta即可):
此时我们就求出最优的weights了,cost function最小.
Regularization
正则化通过增加惩罚项来防止Overfitting:
Regularization prevents overfitting by adding penalty for complexity.
实际等同与在一系列函数中加上了”偏爱”:
Equivalent to imposing a preference over the set of functions that a learner can obtain as a solution.o
在使用regularization的情况下:
cost function = error on the training set + regularization.
对我们的linear regression来说,此时的cost function是:
这里的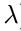
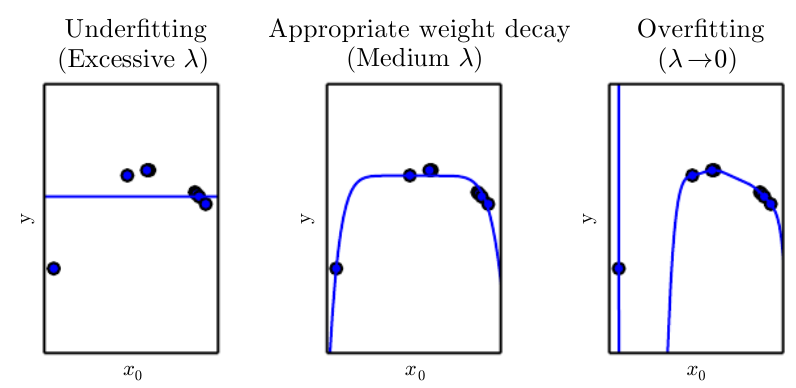
调节正则化参数的大小,可以控制model的capacity:
过大的正则化参数抑制高阶项,相当于使假设趋向于常量.
过小的正则化参数没有抑制作用,model的capacity影响很小.
如下图所示:
当然这里的regularization是非常宽泛的,其形式也可以是多样的.
There are many other ways of expressing preferences for different
solutions, both implicitly and explicitly. Together, these different approaches are known as regularization.
很重要的一点是:
使用正则化可以减小generalization error而不是training error.
Regularization is any modification we make to a learning algorithm that is intended to reduce its generalization error but not its training error.
理论表明没有最优形式的ML algorithm,实际中也没有最好形式的regularization.
Instead we must choose a form of regularization that is well-suited to the particular task we want to solve.
Function estimation
我们假设存在一个function描述输出Y和输入X的关系,那么描述function f就能够使用参数来描述.
Prediction function f can be parametrized by a parameter vector θ.
因此,从training set D 中学习函数f等价于:
estimating θ from D.
estimation的质量可以使用Bias和Variance来衡量,而不是拿真实的parameter和学习到的parameter或者函数之间来对比.
当然这里的设计过程需要相应的domain knwledge,如果参数设计的好的话,即使function的capacity比较小也同样能够获得low generalization error.
Bias
中文叫偏差
where expectation is over all the train sets of size n sampled from the underlying distribution.
Unbiased等价于bias==0:
Variance
中文叫方差
Variance典型的随着training set的增大而减小.
Variance typically decreases as the size of the train set increases.
Bias和variance到底是什么作用呢? Bengio是这样说的,我翻译不好,原话贴上:
Bias measures the expected deviation from the true value of the function or parameter. Variance on the other hand, provides a measure of the deviation from the expected estimator value that any particular sampling of the data is likely to cause.
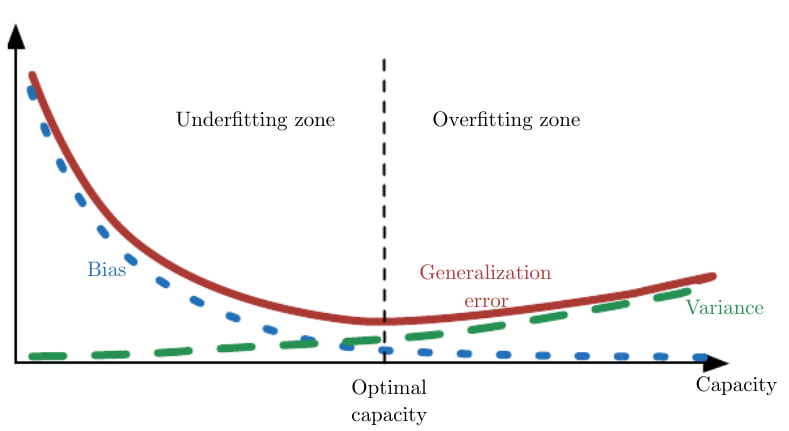
增大model的capacity有可能会增大Variance,但是同时也提高了model去cover到隐藏在data之后的真正的function的可能性.
Increasing the capacity of a learner may also increase variance, although it has better chance to cover the true function.
Bias和Variance都是model的estimation error的一部分,比如:
模型的Capacity和Bias及Variance的关系如下:
这篇就写到这,下篇继续










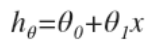

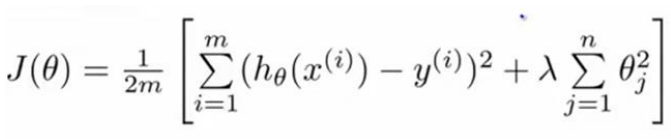
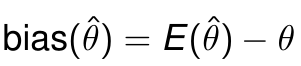
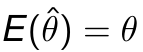
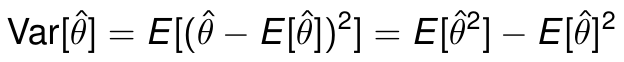
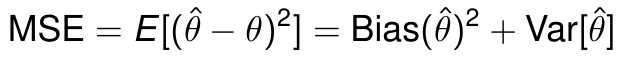














 1512
1512

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








