原理
线性回归,原理很简单,就是拟合一条直线使得损失最小,损失可以有很多种,比如平方和最小等等;
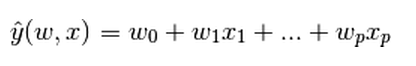
y是输出,x是输入,输出是输入的一个线性组合。
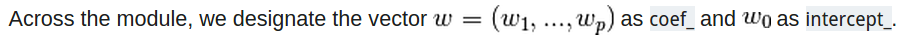
系数矩阵就是coef,截距就是intercept;
例子:
我们的输入和输出是numpy的ndarray,输入是类似于列向量的,输出类似于行向量,看它们各自的shape就是:
输出:y.shape ——>(1,)
输入:x.shape——->(m,1) #m是一个数字
大家记得不要把形式弄错啦,不然可就走不起来了;
下面是个最简单的例子:
>>> from sklearn import linear_model #导入线性模型
>>> clf = linear_model.LinearRegression() #使用线性回归
>>> clf.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2]) #对输入和输出进行一次fit,训练出一个模型
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> clf.coef_ #系数矩阵
array([ 0.5, 0.5])稍微复杂点的例子:
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
# 读取自带的diabete数据集
diabetes = datasets.load_diabetes()
# 使用其中的一个feature
diabetes_X = diabetes.data[:, np.newaxis, 2]
# 将数据集分割成training set和test set
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
# 将目标(y值)分割成training set和test set
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]
# 使用线性回归
regr = linear_model.LinearRegression()
# 进行training set和test set的fit,即是训练的过程
regr.fit(diabetes_X_train, diabetes_y_train)
# 打印出相关系数和截距等信息
print('Coefficients: \n', regr.coef_)
# The mean square error
print("Residual sum of squares: %.2f"
% np.mean((regr.predict(diabetes_X_test) - diabetes_y_test) ** 2))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % regr.score(diabetes_X_test, diabetes_y_test))
# 使用pyplot画图
plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, regr.predict(diabetes_X_test), color='blue',
linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()可以看出,使用还是很简单的,就是准备好数据集:
regr = linear_model.LinearRegression() #使用线性回归
regr.fit(diabetes_X_train, diabetes_y_train) #训练获得一个model
regr.predict(diabetes_X_test) # 预测
regr.score(diabetes_X_test, diabetes_y_test) # 获取模型的score值
OK,就到这,下次继续!





 本文详细介绍了线性回归的基本原理,包括损失函数的选择、系数矩阵和截距的概念,并通过实例展示了如何使用Python和sklearn库实现线性回归模型。从简单到复杂的数据集示例,一步步引导读者掌握线性回归的应用。
本文详细介绍了线性回归的基本原理,包括损失函数的选择、系数矩阵和截距的概念,并通过实例展示了如何使用Python和sklearn库实现线性回归模型。从简单到复杂的数据集示例,一步步引导读者掌握线性回归的应用。
















 8111
8111

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








