CodeForces 369 div2 E. ZS and The Birthday Paradox 数论

E. ZS and The Birthday Paradox

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

ZS the Coder has recently found an interesting concept called the Birthday Paradox. It states that given a random set of 23 people, there is around 50% chance that some two of them share the same birthday. ZS the Coder finds this very interesting, and decides to test this with the inhabitants of Udayland.

In Udayland, there are 2n days in a year. ZS the Coder wants to interview k people from Udayland, each of them has birthday in one of 2ndays (each day with equal probability). He is interested in the probability of at least two of them have the birthday at the same day.

ZS the Coder knows that the answer can be written as an irreducible fraction 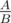. He wants to find the values of A and B (he does not like to deal with floating point numbers). Can you help him?

Input

The first and only line of the input contains two integers n and k (1 ≤ n ≤ 1018, 2 ≤ k ≤ 1018), meaning that there are 2n days in a year and that ZS the Coder wants to interview exactly k people.

Output

If the probability of at least two k people having the same birthday in 2n days long year equals 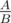 (A ≥ 0, B ≥ 1, 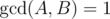), print the A and B in a single line.

Since these numbers may be too large, print them modulo 106 + 3. Note that A and B must be coprime before their remainders modulo106 + 3 are taken.

Examples

input

3 2

output

1 8

input

1 3

output

1 1

input

4 3

output

23 128

Note

In the first sample case, there are 23 = 8 days in Udayland. The probability that 2 people have the same birthday among 2 people is clearly, so A = 1, B = 8.

In the second sample case, there are only 21 = 2 days in Udayland, but there are 3 people, so it is guaranteed that two of them have the same birthday. Thus, the probability is 1 and A = B = 1.

题意：

有2^n天，k个人,求至少2个人生日相同的概率，要求分子分母约分后再对1e6+3取模。

思路“：

1.如果人数比天数多了那就一定有至少2个人是同一天的。

2.算反面，所有人生日都不同，那么第一个人的可能是2^n/2^n,第二个人是(2^n-1)/2^n...第k个人是(2^n-(k-1))/2^n.

所以反面是  

我们要算的是f(n,k) = 1-，然后gcd(a,b) = gcd(b-a,b)  所以f(n,k)要约的数和这个表达式是一样的，考虑到分母是2的指数，所以我们要求分子能提出几个2，然后就可以解决了。还有一个问题是，k很大，那分母的一串乘积怎么办呢，我们注意到mod很小，而且这串积是连续的数，所以当某一个是mod的倍数，那我们就不用接着算了。

代码：

//************************************************************************//
//*Author : Handsome How                                                 *//
//************************************************************************//
//#pragma comment(linker, "/STA    CK:1024000000,1024000000")
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <algorithm>
#include <sstream>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <string>
#include <ctime>
#if defined(_MSC_VER) || __cplusplus > 199711L
#define aut(r,v) auto r = (v)
#else
#define aut(r,v) __typeof(v) r = (v)
#endif
#define foreach(it,o) for(aut(it, (o).begin()); it != (o).end(); ++ it)
#define fur(i,a,b) for(int i=(a);i<=(b);i++)
#define furr(i,a,b) for(int i=(a);i>=(b);i--)
#define cl(a) memset((a),0,sizeof(a))
#define min(a,b) ((a)<(b)?(a):(b))
#define max(a,b) ((a)>(b)?(a):(b))
#ifdef HandsomeHow
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define dbg(x) cout << #x << " = " << x << endl
#else
#define debug(...)
#define dbg(x)
#endif
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair <int, int> pii;
const int inf=0x3f3f3f3f;
const double eps=1e-8;
const ll mod=1000003;
const double pi=acos(-1);
inline void gn(long long&x){
    int sg=1;char c;while(((c=getchar())<'0'||c>'9')&&c!='-');c=='-'?(sg=-1,x=0):(x=c-'0');
    while((c=getchar())>='0'&&c<='9')x=x*10+c-'0';x*=sg;
}
inline void gn(int&x){long long t;gn(t);x=t;}
inline void gn(unsigned long long&x){long long t;gn(t);x=t;}
ll gcd(ll a,ll b){return a? gcd(b%a,a):b;}
ll powmod(ll a,ll x,ll mod){a%=mod;ll t=1ll;while(x){if(x&1)t=t*a%mod;a=a*a%mod;x>>=1;}return t;}
// (づ°ω°)づe★
//-----------------------------------------------------------------
ll n,k;
int main(){
#ifdef HandsomeHow
    //freopen("data.in","r",stdin);
    //freopen("data.out","w",stdout);
    time_t beginttt = clock();
#endif
	cin>>n>>k;
	if(n<=60 && k>(1ll<<n))
	return 0*printf("1 1\n");//人比天数多 
	ll t = k;
	ll ys = 0ll;
	ll d = powmod(2,n,mod);//2^n
	--t;
	ll now = 2ll;
	while(now<=t){
		ys += (t/now);		//分子含2的个数 
		now<<=1;
	}
	ll ny = powmod(2ll,mod-2ll,mod);//2关于mod的逆元 
	ll fz = 1, fm = 1;
	fur(i,2,k){
		fz = fz * (d-i+1) % mod;
		if(fz == 0) break;
	}
	fz = fz * powmod(ny,ys,mod) % mod;
	fm = powmod(2ll,n,mod);
	fm = powmod(fm,k-1,mod);
	fm = fm * powmod(ny,ys,mod) % mod;
	fz = fm - fz;
	if(fz<0) fz+=mod;
	printf("%I64d %I64d\n",fz,fm);
#ifdef HandsomeHow
	time_t endttt = clock();
    debug("time: %d\n",(int)(endttt - beginttt));
#endif
	return 0;
}