【学习笔记】K-L变换和PCA的区别

K-L变换和PCA的区别是什么？

学习模式识别，大家自然会想到这样一个并不重要的问题。老师们讲课时将这两个概念做了统一处理，wiki上也直接统一了词条。这样做的原因很好理解，大概即使它们有区别，也是极其细微的，是不需要纳入考虑的。之所以探究这个问题，更多的还是为了能加深对这些算法的理解。

 

=======================================================

 

先引述一种关于两者是否有区别的观点：

Simone Orcioni  · Università Politecnica delle Marche
None.
Take advantage of this link:
http://en.wikipedia.org/wiki/Karhunen%E2%80%93Lo%C3%A8ve_theorem

"The above expansion into uncorrelated random variables is also known as the Karhunen–Loève expansion or Karhunen–Loève decomposition. The empirical version (i.e., with the coefficients computed from a sample) is known as the Karhunen–Loève transform (KLT), principal component analysis, proper orthogonal decomposition (POD), Empirical orthogonal functions (a term used in meteorology and geophysics), or the Hotelling transform."

他引述wiki对KL理论（KL转换）的介绍“...以上对不相关随机变量的分解也被称为KL分解。它的实证版本（换言之，用到了通过样本求得的参数）被称为KLT、PCA、特征正交分解（POD）、经验正交函数（用于气象学和地理学）或霍特林变换。”

 

这是一种较为普遍的说法，甚至在PRML中也是使用的类似描述，认为PCA与KL是同样的东西。果真如此，那为什么会有这么多叫法呢？我们再来看看另一种解释。这是CSDN上看到的说法是（相同博文有两篇，就不链接了）：

 

PCA的变换矩阵是协方差矩阵，K-L变换的变换矩阵可以有很多种（二阶矩阵、协方差矩阵、总类内离散度矩阵等等）。当K-L变换矩阵为协方差矩阵时，等同于PCA。

这个解释与课本的编排能很好的结合起来。课本基本没有提PCA，但是关于KLT的讲解是按照这样的顺序：首先引入离散KL展开（通过自相关矩阵求得转换矩阵），再过渡到降维（此时计算则使用协方差阵）的KL变换，并点明，如果平移坐标系使以样本均值为原点时，协方差阵等于自相关矩阵。其后的下一讲则介绍了，使用不同的散布矩阵完成KL变换，会得到不同的效应，其中总体散布矩阵即前述协方差矩阵。

 

再来看看国外网站上另一个哥们说的：

Fabrice Clerot  · Orange Labs

they are quite close but with a slight diffference : PCA analyzes the spectrum of the covariance matrix while KLT analyzes the spectrum of the correlation matrix

即，两者区别在于PCA分析协方差矩阵而KLT分析相关矩阵。

 

这是更为具体的一种解释：

 

Pradeep Gupta  · Jaypee University of Information Technology
PCA depend on the scaling of the variables and applicability of PCA is limited by certain assumptions made in its derivation. The claim that the PCA used for dimensionality reduction preserves most of the information of the data is misleading. Indeed, without any assumption on the signal model, PCA cannot help to reduce the amount of information lost during dimensionality reduction, where information was measured using Shannon entropy.

The coefficients in the KLT are random variables and the expansion basis depends on the process. In fact, the orthogonal basis functions used in this representation are determined by the covariance function of the process. KLT adapts to the process in order to produce the best possible basis for its expansion.it reduces the total mean-square error resulting of its truncation. Because of this property, it is often said that the KL transform optimally compacts the energy. The main implication and difficulty of the KL transformation is computing the eigenvectors of the linear operator associated to the covariance function, which are given by the solutions to the integral equation.

The integral equation thus reduces to a simple matrix eigenvalue problem, which explains why the PCA has such a broad domain of applications.

他说，PCA依赖于变量的展开（不知如何翻译）且其应用受限于一些由原始推导过程中的具体假设。关于PCA用于降维能保留绝大部分信息的说法是误导的。事实上，如果没有对信号模型的任何假设，PCA对减少降维过程的信息丢失没有帮助（这里用香农熵测量信息量）。

而KLT的参数为随机变量，且其展开的基础取决于过程（随机过程，理解为样本，下文有详注）。事实上，用于描述的正交基函数是由过程的协方差函数确定的。KLT去适应这个过程（随机过程），以期产生最佳的展开基。这样可以减少降维产生的总均方差。由于这个特性，常说KLT能最好得压缩能量。KLT主要的内容和难点在于计算关于协方差函数的线性操作的特征向量，即由积分方程求得的解。

积分方程因此简化为简单的矩阵特征值问题，这解释了为什么PCA有如此广泛的应用。

 

=======================================================

 

这些网上的说法并没有解释清楚，还增添了疑惑，于是参考wiki。解决关于几个矩阵的关系，以及KLT与PCA的关系

 

一、散布矩阵、协方差矩阵、自相关矩阵

散布矩阵定义参考机器学习_刘伟翻译的wiki条目。其本身的定义很简单，

 

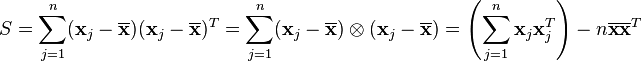
此外还可以更具体的定义，如总体散布矩阵、类内散布矩阵、类间散布矩阵等。其中总体散布矩阵的定义为

S_t = E{ (x - m_0) *(x - m_0)T }

这个定义实际上就是协方差矩阵，即散布矩阵除以样本数n。也就是说样本的协方差矩阵也就等于样本的总体散布矩阵，对总体散布矩阵的KL变换就是对协方差矩阵的KL变换。

 

自相关矩阵的定义参见维基autocorrelation matrix 。有

其中自相关函数R_xx(n)的概念参见维基Autocorrelation#Signal_processing 。

对于离散情况有

其中为实数时，函数y杠=y。

注意到自相关矩阵与协方差矩阵的关系为

即，若将样本平移到均值为原点的坐标系中，则此时协方差阵与自相关阵相同。

 

以上就理清了协方差矩阵分别于总体散布矩阵和自相关矩阵的关系。

 

二、KLT 、 PCA

由于wiki中KL Transform词条直接重定向到了PCA，便参考Karhunen–Loève theorem词条（KL原理，根据内容译成KL展开）。

KL展开是随机过程的理论，将随机过程描述成无穷个正交函数的线性结合。其重要性在于，得到的结果拥有最小均方差。

不同于傅里叶级数展开（系数为实数&展开基函数由正余弦函数组成），KL展开的系数是随机变量，且展开基函数由随机过程决定。实际上，这里的正交基函数是由随机过程的协方差函数确定的。可以认为，KL展开是根据随机过程产生最佳基函数。

完成KL展开，就需要求出正交基函数。由于线性映射等各种性质，可知未知量满足均匀弗雷德霍姆积分方程，即可通过解方程求出基函数。

在阅读wiki的过程中，我发现百科里涉及到的术语有些陌生，比如stochastic process，包括上文网上回答中的process，查询才知道数学上概念即“随机过程”，是一系列随机变量/随机函数的集合，也就是说样本也属于随机过程。

继续阅读发现，KLtheorem词条中居然也有PCA的内容，读罢惊喜地发现KLT与PCA的区别基本就已经明了了：

KLT的计算过程十分复杂，就在于积分方程的求解。然而，当应用于离散随机过程（即多个样本）中，正交基满足的原本连续的积分等式，成了离散的求和，这就极大简化了计算，也扩张了实际应用的领域。

在PCA词条中说，根据不同的应用域，PCA在信号处理中被叫做离散KL变换、多元质量控制中为霍尔特变换、机器工程中为本征正交分解等。

归纳一下，KLT是一种对于连续或离散的随机过程都可进行的变换，PCA则是KLT处理离散情况的算法；定义上KLT比PCA广泛，而实际上PCA比KLT实用。

 

=======================================================

 

最后再来验证网友的说法：

关于协方差阵与自相关阵，两者只差对样本均值的平移量，而wiki里的KL变换都需要先平移样本，故真正应用中PCA与KLT在这一点没有差别；而关于那个篇幅很长的回答，内容则基本来自wiki，因此也没有必要再说明了。

无论说说KLT与PCA有区别与否，都有其道理，我们只用知道，实际编程中可以不考虑两者的区别，就足够了。

 

 

 

p.s.     PCA的发明时间比KLT早得多

P.s.2   wiki真是是好用又靠得住啊！