快速傅立叶变换（FFT）的C++实现与Matlab实验

最新推荐文章于 2024-09-29 23:59:18 发布

Rappy

最新推荐文章于 2024-09-29 23:59:18 发布

阅读量3.3w

点赞数 2

分类专栏：程序代码算法文章标签： matlab fft c++ float output 算法

本文链接：https://blog.csdn.net/Rappy/article/details/1700829

版权

本文介绍了快速傅立叶变换（FFT）的基本原理，并展示了如何使用C++和Matlab进行实现。通过比较C++程序和Matlab的运算结果，分析了两者之间的误差来源。

摘要由CSDN通过智能技术生成

借佳佳的《复变函数与积分变换》看了两天，总算弄懂了傅立叶变换是怎么一回事。但是要实现快速傅立叶变换却不需要弄懂那么多东西，看看《算法导论》里面的第 30 章“多项式与快速傅立叶变换”就可以了。不过《算法导论》的介绍和标准的有点小小的不同，就是旋转因子刚好反过来了，不过还是等效的。

标准的离散傅立叶 DFT 变换形式如：

y_k=Σ_j=0^n-1 a_jω_n^-_kj= A (ω_n^-_k).

（ω_n^_k 为复数 1 的第 k 个 n 次方根，且定义多项式 A (x) = Σ_j=0^n-1 a_jx^j）

而离散傅立叶逆变换 IDFT (Inverse DFT)形式如： a_j=(Σ_k=0^n-1 y_kω_n_^kj)/n .

以下不同颜色内容为引用并加以修正：

快速傅立叶变换（Fast Fourier Transform，FFT）是离散傅立叶变换（Discrete Fourier transform，DFT）的快速算法，它是根据离散傅立叶变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。它对傅立叶变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。
设 X_n为 N 项的复数序列，由 DFT 变换，任一 X_i 的计算都需要 N 次复数乘法和 N -1 次复数加法，而一次复数乘法等于四次实数乘法和两次实数加法，一次复数加法等于两次实数加法，即使把一次复数乘法和一次复数加法定义成一次“运算”（四次实数乘法和四次实数加法），那么求出 N 项复数序列的 X_i ，即 N 点 DFT 变换大约就需要 N²次运算。当 N =1024 点甚至更多的时候，需要 N²= 1048576 次运算，在 FFT 中，利用 ω_n的周期性和对称性，把一个 N 项序列（设 N 为偶数），分为两个 N / 2 项的子序列，每个 N / 2点 DFT 变换需要 (N / 2)²次运算，再用 N 次运算把两个 N / 2点的 DFT 变换组合成一个 N 点的 DFT 变换。这样变换以后，总的运算次数就变成 N + 2 * (N / 2)²= N + N²/ 2。继续上面的例子，N =1024 时，总的运算次数就变成了525312 次，节省了大约 50% 的运算量。而如果我们将这种“一分为二”的思想不断进行下去，直到分成两两一组的 DFT 运算单元，那么N 点的 DFT 变换就只需要 N * log₂N 次的运算，N = 1024 点时，运算量仅有 10240 次，是先前的直接算法的1% ，点数越多，运算量的节约就越大，这就是 FFT 的优越性。

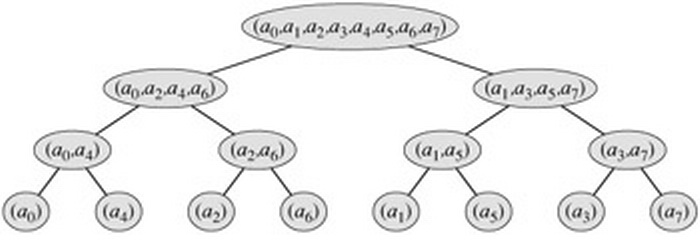
FFT 的实现可以自顶而下，采用递归，但是对于硬件实现成本高，对于软件实现都不够高效，改用迭代较好，自底而上地解决问题。感觉和归并排序的迭代版很类似，不过先要采用“位反转置换”的方法把 X_i 放到合适的位置，设 i 和 j 互为s = log₂N 位二进制的回文数，假设 s = 3, i = (110)₂ = 6, j = (011)₂= 3, 如果 i ≠ j , 那么 X_i和 X_j应该互换位置。（关于这个回文数的生成，是很有趣而且是很基本的操作，想当初偶初学 C++ 的时候就有这样的习题。）当“位反转置换”完成后，先将每一个X_i 看作是独立的多项式，然后两个两个地将它们合并成一个多项式（每个多项式有 2 项），合并实际上是“蝶形运算”（Butterfly Operation, 参考《算法导论》吧^_^），继续合并（第二次的每个多项式有 4 项），直到只剩下一个多项式（有 N 项），这样，合并的层数就是 log₂N ，每层都有 N 次操作，所以总共有 N * log₂N 次操作。迭代过程如下图所示，自底而上。