在逆序对的问题中,如果采用暴力求解的方法,一般也是有效的,但是O(n2)时间复杂度实在是难以接受的。但是对于逆序对问题,却有一个看似不想关的算法来解决–归并排序。时间复杂度和空间复杂度完全与归并排序一样,只是在归并过程中,添加了一个变量,对于逆序对的数目进行了记录。这样就将时间复杂度降低到了O(nlogn)。
原理
因为逆序对的数目可能存在平方数个逆序对,因此要想将逆序对数目求解的复杂度降低到O(nlogn),就不能对每一个逆序对进行计算。根据归并排序思想,使用归并求解逆序对时,将会在将两个有序数组合并成一个有序数组的过程中,记录逆序对的数目,其他如数组划分和排序过程同归并排序。
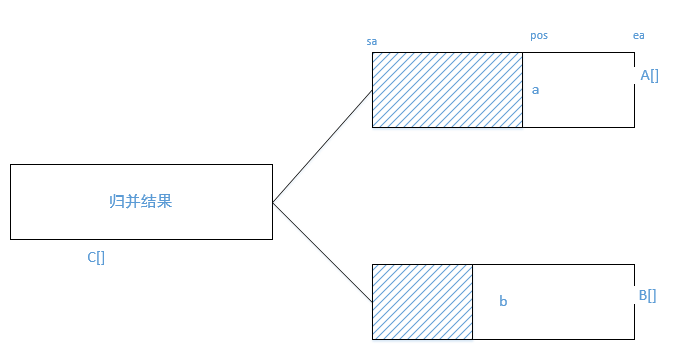
在归并排序的合并步骤中,假设将两个有序数组A[] 和有序数组B[] 和并为一个有序数组C[]。计算逆序对问题转换为计算逆序对(a,b)的问题,其中a来自A[], b来自B[]。当a < b的时候,不计数,当a>b的时候(a,b)就是逆序对,由于A[]是有序的,那么A[]中位于a之后的元素对于B[]中的元素b也形成了逆序对,于是对于逆序对(a,b),(假设A[]的起始下标为sa,结束下标为ea,a的下标为pos)实际上合并成C[]后会会产生ea-pos+1个逆序对。
也就是说,合并过程中,每次出现一对这样的(a,b),逆序对数目sum = sum + ea-pos+1 ;
根据这样的原理,再给予对归并排序的理解,将上面的计算公式加入到归并排序中,就可以在O(nlogn)的时间复杂度里计算出一个给定数字序列中逆序对的数目。
示例代码
#include<iostream>
#define N 100000
using namespace std;
void merge(int arr[],int start,int mid,int end,int temp[],long long *count){
int index = 0,index1 = 0,index2 = 0;
index = 0; index1 = start; index2 = mid+1;
while((index1<=mid) && (index2<=end)){
if(arr[index1] <= arr[index2]){
temp[index++] = arr[index1++];
}
else{
temp[index++] = arr[index2++];
//ans+=e1-p1+1;
(*count) = (*count) + mid - index1 + 1;
}
}
while(index1<=mid)
temp[index++] = arr[index1++];
while(index2<=end)
temp[index++] = arr[index2++];
for(int i=0;i<index;i++){
// 复制也是递归进行的,所以并不是从start开始到end
arr[start+i] = temp[i];
}
}
void mergeSort(int arr[],int start,int end,int temp[],long long *count){
if(start<end){ // 递归出口
int mid = 0;
mid = (start+end)>>1;
mergeSort(arr,start,mid,temp,count);
mergeSort(arr,mid+1,end,temp,count);
merge(arr,start,mid,end,temp,count);
}
}
int main(){
long long count = 0;
int m = 0;
cin>>m;
int *a = new int[m];
for(int i=0;i<m;i++){
cin>>a[i];
}
int *temp = new int[m];
mergeSort(a,0,m-1,temp,&count);
delete []a;
delete []temp;
cout<<count<<endl;
return 0;
}
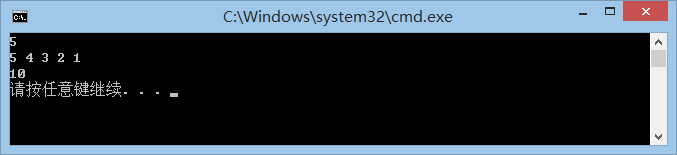
输入格式为:先输入一个数字代表数组的长度,回车,接下来依次输入以空格分割的n个数组元素。输出就是该数组的逆序对数目。






















 466
466

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








