题目:http://acm.hdu.edu.cn/showproblem.php?pid=4773
题意:给定两个圆,告诉半径和圆心,它们是相离的,在这两个圆外给定一个点p,求符合条件:过点p的圆且与已知的两个
圆外切的所有圆的总数和它们的圆心坐标和半径。
分析:根据题意,我们设已知两个圆的半径分别为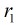
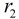
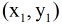
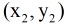
并设要求的圆的圆心为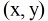
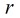
然后,现在的问题就是来解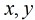
那么,怎么用反演变换来做? 首先,得知道什么是反演变换以及它有什么性质。
反演的定义:
已知一圆C,圆心为O,半径为r,如果P与P’在过圆心O的直线上,且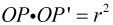
反演的性质:
(1)除反演中心外,平面上的每一个点都只有唯一的反演点,且这种关系是对称的,位于反演圆上的点,保持在原处,位于
反演圆外部的点,变为圆内部的点,位于反演圆内部的点,变为圆外部的点。 举个最简单的例子,区间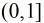
半径,那么反演后的区间就是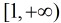
(2)任意一条不过反演中心的直线,它的反形是经过反演中心的圆,反之亦然,特别地,过反演中心相交的圆,变为不过反
演中心的相交直线。
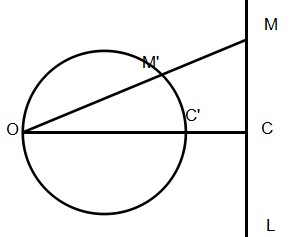
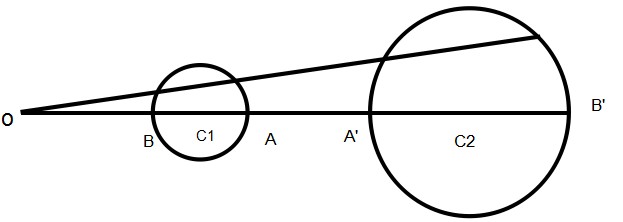
定理:不过反演中心的圆,它的反形是一个圆,反演中心是这两个互为反形的圆的一个位似中心,任意一对反演点是逆对应
点。用图形来解释,如下图:
那么,对于一个不过反演中心的圆,怎样求它的反形圆?
很容易知道我们只需要求出反形圆的圆心和半径就可以了。
对于上图我们设圆C1的半径为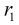
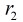
那么根据反演的定义有:
那么,消去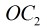
这样我们就得到了反形圆的半径,那么还要求反形圆的圆心。
由于C1和O两点的坐标已知,而且我们知道O,C1,C2位于同一直线上,那么很明显对于C2的坐标,我们可以这样计算:
设O的坐标为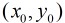
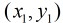
那么有:
至于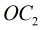
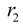
由于本题的做法是这样的,先以点P为为反演中心,反演半径随便设置都可以,为了计算方便就设为1,把圆C1和圆C2反演后再求这两个圆的
公切线,再把这个公切线反演回去,那么就是一个过点P的圆,且与原来的C1和C2相切。
那么接下来就是如何计算两个圆的公切线了。这里只需要考虑公切线在同一侧的情况。那么,这个自己画图就能很容易计算了。
找到公切线后还要把它反演成圆,这个圆还经过P点,那么很容易得到了。
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>
using namespace std;
double const eps = 1e-8;
struct Point
{
double x,y;
Point(double a = 1.0,double b = 1.0):x(a),y(b){}
Point operator + (const Point &a)
{
return Point(x+a.x,y+a.y);
}
Point operator - (const Point &a)
{
return Point(x-a.x,y-a.y);
}
Point operator * (const double a)
{
return Point(a*x,a*y);
}
Point Trans()
{
return Point(-y,x);
}
void Input()
{
scanf("%lf%lf",&x,&y);
}
} ;
struct Circle
{
Point o;
double r;
Circle(Point a = Point(),double b = 1.0):o(a),r(b) {}
Point getPoint(double alpha)
{
return o + Point(r*cos(alpha),r*sin(alpha));
}
void Input()
{
o.Input();
scanf("%lf",&r);
}
void Output()
{
printf("%.8lf %.8lf %.8lf\n",o.x,o.y,r);
}
} ;
Point p;
Circle c[15];
double dist(Point A,Point B)
{
return sqrt((A.x-B.x)*(A.x-B.x) + (A.y-B.y)*(A.y-B.y));
}
double cross(Point A,Point B,Point C)
{
return (B.x-A.x)*(C.y-A.y) - (B.y-A.y)*(C.x-A.x);
}
int sign(double x)
{
return (x > eps) - (x < -eps);
}
Circle Inverse(Circle C)
{
Circle T;
double t = dist(C.o,p);
double x = 1.0 / (t - C.r);
double y = 1.0 / (t + C.r);
T.r = (x - y) / 2.0;
double s = (x + y) / 2.0;
T.o = p + (C.o - p) * (s / t);
return T;
}
void add(Point a,Point b,int &k)
{
double t = cross(a,p,b);
if(t < 0) t = -t;
double d = dist(a,b);
t /= d;
if(t > eps)
{
double w = 0.5 / t;
Point dir = (b-a).Trans();
Point a1 = p + dir * (w / d);
Point b1 = p - dir * (w / d);
if(fabs(cross(a,b,a1)) < fabs(cross(a,b,b1)))
c[k++] = Circle(a1,w);
else
c[k++] = Circle(b1,w);
}
}
int Work()
{
c[0] = Inverse(c[0]);
c[1] = Inverse(c[1]);
if(c[1].r > c[0].r) swap(c[1],c[0]);
Point v = c[1].o - c[0].o;
double alpha = atan2(v.y,v.x);
double d = dist(c[0].o,c[1].o);
double beta = acos((c[0].r - c[1].r) / d);
int k = 2;
Point a = c[0].getPoint(alpha + beta);
Point b = c[1].getPoint(alpha + beta);
if(sign(cross(a,c[0].o,b)) == sign(cross(a,p,b)) &&
sign(cross(a,c[1].o,b)) == sign(cross(a,p,b)))
add(a,b,k);
a = c[0].getPoint(alpha - beta);
b = c[1].getPoint(alpha - beta);
if(sign(cross(a,c[0].o,b)) == sign(cross(a,p,b)) &&
sign(cross(a,c[1].o,b)) == sign(cross(a,p,b)))
add(a,b,k);
return k - 2;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
c[0].Input();
c[1].Input();
p.Input();
int num = Work();
printf("%d\n",num);
for(int i=0;i<num;i++)
c[i+2].Output();
}
return 0;
}








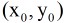
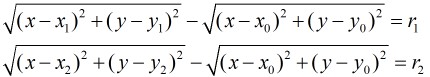
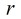
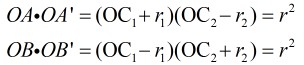
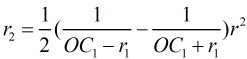
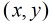
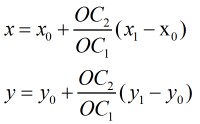














 998
998

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








